What you wanted to know about the optical flow, but hesitate to ask

Optical flow (Optical flow) - a technology used in various areas of computer vision to determine shifts, segmentation, object selection, video compression. However, if we want to implement it quickly in our project, having read about it on Wikipedia or anywhere else, then, most likely, we will very quickly come across the fact that it works very poorly and fails when determining shifts of the order of 1-2. pixels (at least it was with me). Then we turn to ready implementations, for example, in OpenCV. There, it is implemented by various methods and it is completely incomprehensible that the PyrLK abbreviation is better or worse than the designation Farneback or something like that, and you will have to figure out the meaning of the parameters, which in some implementations are very many. And, interestingly, these algorithms somehow work, in contrast to what we wrote ourselves. What is the secret?

What is optical flow?

Optical flow (OD) is an image of visible movement, representing the shift of each point between two images. In fact, it is a velocity field (since the shift with a scale accuracy is equivalent to an instantaneous velocity). The essence of the OP is that for each point of the image 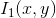is such a shift (dx, dy), so that the starting point corresponds to the point on the second image 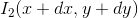. How to determine the correspondence of points is a separate question. For this we need to take some function of the point, which does not change as a result of the displacement. It is usually considered that the point maintains the intensity (i.e., brightness or color for color images), but can be considered the same points for which the value of the gradient, Hessian, its value or its determinant, Laplacian, and other characteristics is preserved. Obviously, the conservation of intensity fails if the illumination or angle of incidence of the light changes. Nevertheless, if we are talking about a video stream, then, most likely, the illumination between two frames will not change much, if only because a short period of time passes between them. Therefore, often use the intensity as a function, persisting at the point.

According to this description, you can confuse OP with the search and comparison of characteristic points. But these are different things, the essence of the optical flow is that it does not look for any particular points, but by the parameters of the images it tries to determine where an arbitrary point has shifted.

There are two options for calculating the optical flux: dense (dense) and selective (sparse). The Sparse stream calculates the shift of individual predetermined points (for example, points allocated to a certain feature detector), a dense stream counts the shift of all points of the image. Naturally, the sample stream is calculated faster, but for some algorithms the difference is not that big, and for some tasks it is necessary to find the stream in all points of the image.
')
For degenerate cases, simpler methods for determining shear can be applied. In particular, if all points of the image have the same shift (the image is shifted entirely), then you can apply the phase correlation method: calculate the Fourier transform for both images, find the convolution of their phases and determine the shift using it (see en.wikipedia.org / wiki / Phase_correlation ). You can also apply block matching: find a shift that minimizes the rate of difference of images in the window. In its pure form, such an algorithm will work for a long time and is unstable to turns and other distortions. The English Wikipedia classifies the listed algorithms as different options for calculating the optical flow, but this does not seem to me to be too correct, since these algorithms can be used for other purposes and do not completely solve this problem. We will call optical flow methods based on local characteristics of images (what is called differential methods in the English wikipedia).

Standard approach (Lucas-Canada method)

The mathematical description of the algorithm is given in sufficient detail in this article , but it only deals with theoretical aspects.

Consider a mathematical model of the optical flow, assuming that the point has not changed as a result of the displacement.

Let be 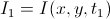Is the intensity at some point (x, y) in the first image (i.e. at time t). In the second image, this point shifted to (dx, dy), while the time dt passed, then 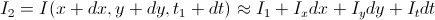- this we have decomposed according to Taylor the intensity function to the first term (later it will be mentioned, why only to the first), here 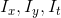- partial derivatives with respect to coordinates and time, that is, in fact 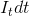- change the brightness at the point (x, y) between two frames.

We believe that the point has preserved intensity, which means
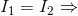
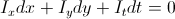
We get one equation with two unknowns (dx and dy), which means it is not enough to solve, that is, you cannot go far on this equation.

The simplest solution to the problem is the Lucas-Canada algorithm. In our image, objects larger than 1 pixel are in the image, which means that, most likely, in the vicinity of the current point, other points will have approximately the same shifts. Therefore, we take a window around this point and minimize (according to the OLS) in it the total error with weights distributed according to Gauss, that is, so that the pixels closest to the object under investigation have the greatest weight. After the simplest transformations, we get a system of 2 equations with 2 unknowns:

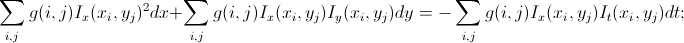
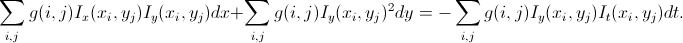
As is known, this system has a unique solution not always (although very often): if the determinant of the system is zero, then there are no solutions or an infinite number. This problem is known as the Aperture problem - the ambiguity of the shift with a limited field of view for periodic images. It corresponds to the case when a fragment of an image in which a certain cyclicality is present enters the field of view; here too, the person will not be able to unambiguously determine where the picture has shifted. The problem is that due to noise in such ambiguous situations, we will get not a zero determinant, but a very small one, which most likely leads to very large values ​​of the shift, which is not particularly correlated with reality. So at a certain stage you just need to check whether the determinant of the system is small enough, and, if anything, do not consider such points or mark them as erroneous.

Why does not it work?

If we stop at this stage and implement this algorithm, it will work successfully. But only if the shift between adjacent images is very small, about 1 pixel, and not always. (To analyze the quality, synthetic sequences with different relative shifts were generated, and this shift can be expressed by a non-integer number of pixels, then the resulting image is interpolated appropriately) The error will be large at 2 pixels, and if 3 or more, the result will be inadequate. What is the matter?

Here we were set up by mathematics. She instilled in us the feeling that all the functions around are continuous and differentiable many times. In general, we were taught at the institute to approximate a function in a neighborhood of a point using the Taylor formula, and we use it 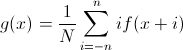thoughtlessly everywhere. And now let's think about what is the physical meaning of the derivatives in this place? We want to use them to determine the change in the value of the function in a finite neighborhood of a point, and the derivative gives an idea of ​​the infinitesimal neighborhood. To expand this neighborhood, a higher order of derivatives could be added to the Taylor expansion, but this will lead to non-linearities in the system, which makes it significantly more difficult to solve, and the advantages will be doubtful, especially since in practice we are not dealing with continuous multiply differentiable functions, and with generally not clear what discrete functions. Therefore, it would be more logical to look for the function g (x), for which in our discrete case, as accurately as possible, f (x) + g (x) = f (x + 1), f (x) + 2g (x) = f (x +2), f (x) - g (x) = f (x-1), and so on. Thus, in this case, we need not a derivative, but some linear function most closely lying to the points of the original function. Simple math calculations lead to solution where 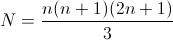. If we built a derivative of one neighboring point on each side, then we are lucky: in this case, the formula coincides with the formula for approximate calculation of the derivatives: g (x) = (f (x + 1) - f (x-1)) / 2. What is characteristic, in OpenCV, when calculating the optical flow of Lucas-Canada, it is this formula that is used; we will return to this later. But if we take more points, then the formula is no longer at all like the classical difference schemes for the first derivative.

Obviously, if we build this function, for example, on three neighboring points to the left and right of the original one, then it does not depend in any way on further points, and, accordingly, if we shift more than three points, we will often get inadequate results . And also, the greater the number of points on which we build this function, the greater is the average deviation of the resulting line from the points used - again, because we do not have linearly changing images, but the devil knows which ones. In practice, shifts greater than 2 pixels already give an inadequately large error, no matter how many points we take.

Another weak point of the algorithm is that we again have to deal not with smooth continuous functions, but with arbitrary, and even discrete ones. Therefore, on some fragments of the image, the intensity may “jump” at all without obvious patterns, for example, at the boundaries of objects, or because of noise. In this case, no function g (x) can sufficiently accurately describe the changes in the image in a neighborhood of a point. In order to fight this (at least partially), the original image is proposed to be smeared, and it will be useful to smear it quite strongly, that is, it is better to use not even the beloved gaussian blur (averaging with weighting factors), but just a box filter (uniform averaging over the window). ), and even several times in a row. The smoothness of the image for us is now more important than detail.

However, these measures also will not save us from limiting the detected shift of 2-3 pixels. And by the way, in OpenCV 1.0 there was such an implementation of the optical flow, and it worked only in ideal conditions on very small shifts.

What to do?

In total, the usual Lucas-Canada well defines small changes, such that the picture is similar to its linear approximation. To fight this, let's use the standard CV technique — multi-scaling: we will build a “pyramid” of images of different scale (almost always scaling 2 times on each axis, it’s easier to count) and go through them with optical flow from a smaller image to a larger one. , then the detected small shift in the small image will correspond to the large shift in the large image. On the smallest image, we find a shift of no more than 1-2 pixels, and moving from a smaller scale to a larger one, we use the result from the previous step and specify the shift values. Actually, in OpenCV it is implemented by the function calcOptFlowPyrLK. Using this pyramidal algorithm allows us not to bother with calculating the linear approximation over many points: it’s easier to take more levels of the pyramid, and at each level to take a rather crude approximation of this function. Therefore, in OpenCV, and is calculated only by two adjacent points. Therefore, in relation to this implementation of the algorithm, our conclusions about the advantage of the approximating function over the derivative turned out to be useless: for such a number of reference points, the derivative is the best approximating function.

And what else happen?

This algorithm is not the only option to calculate the optical flow. In OpenCV, in addition to the Lucas-Canada stream, there is also the Farneback and SimpleFlow stream, also often referring to the Horn – Schunck algorithm.

The Horn – Schunck method is somewhat more global than the Lucas-Canada method. It relies on the assumption that the optical flux will be fairly smooth over the entire image. From the same equation 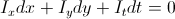proposed to move to the functional 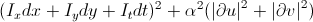, that is, to add a requirement for the absence of abrupt changes in shifts with a weighting factor α. Minimizing this functional leads us to a system of two equations: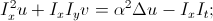



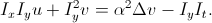
In these equations, the Laplacian is proposed to be calculated approximately: 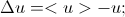- the difference with the average value. We obtain the system of equations that we write for each pixel and solve the general system iteratively: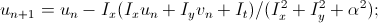



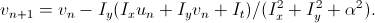
In this algorithm, they also suggest using multi-scaling, and it is recommended that images be scaled not 2 times, but with a coefficient of 0.65

This algorithm was implemented in the first versions of OpenCV, but was later abandoned.

Farneback proposed to approximate the change in intensity in the neighborhood using a quadratic form: I = xAx + bx + c with a symmetric matrix A (in fact, considering the Taylor expansion to the first term, we took a linear approximation I = bx + c, so now we are like once decided to improve the accuracy of the approximation) If the image has moved within this neighborhood, then 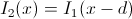, we substitute into quadratic decomposition, we open brackets, we get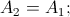


.

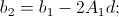
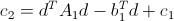Now we can calculate the values ​​of A, b, c in both pictures, and then this system will become redundant with respect to d (the first equation is especially confusing), and in general d can be obtained from the second equation: 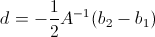. It is necessary to resort to the following approximation: 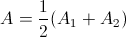. We denote for simplicity 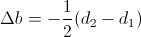Then we just get .

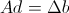To compensate for the noise in the calculation, let us again refer to the assumption that in the vicinity of the point under study all points have more or less the same shift. Therefore, again, we integrate the error 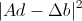over the window with Gaussian weight coefficients w , and we find the vector d minimizing this total error. Then we get the optimal value. 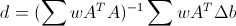and the corresponding minimum error 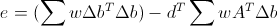. That is, we need to count for each point 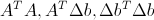, average over the window, invert the matrix and get the result. Accordingly, these works can be calculated for the entire picture and use the pre-calculated values ​​for different points, that is, this is exactly the case when it makes sense to consider a dense stream.

As usual, this algorithm has a number of modifications and improvements, primarily allowing the use of known a priori information - a given initial approximation of the flow - and, again, multi-scaling.

The SimpleFlow method is based on the following idea: if we still cannot determine a shift larger than the size of the window for which we were looking for derivatives, then why bother with calculating derivatives at all? Let's just find the most similar point in the window! And to resolve ambiguities and to compensate for noise, we will take into account that the flow is continuous and in the vicinity of this point all points have almost the same shift. And again we will solve the problem with the size of the window due to multi-scaling.

More strictly, the algorithm sounds like this: for all points in the window, there is a function of “energy”, which is responsible (with inverse logarithmic dependence) for the probability of the transition of the starting point to this point: 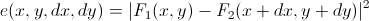. Further, it is considered the convolution of this energy with a Gaussian window. 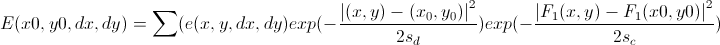and find the values ​​(dx, dy) that minimize this function. To obtain subpixel accuracy, a small neighborhood of the found optimal point (dx, dy) is considered and the peak of the function of energy is sought in it as the peak of a paraboloid. And, as mentioned above, this procedure is performed for a pyramid of scaled images. They also offer clever methods for speeding up calculations in the algorithm, but it is already interesting for anyone to figure it out for themselves. For us, it is important that due to this, this algorithm is (theoretically) fast enough with good accuracy. And it does not have such a problem as the previous ones, that the greater the shift, the worse it is detected.

And if you take no intensity?

It was said above that the correspondence between the points can be determined by different quantities, so why do we only consider the intensity? But because any other value can be reduced to it: we simply filter the images with the appropriate filter and feed the filtered images as input to the algorithms described above. Accordingly, if you want to use an optical stream, first think, in your conditions, which characteristic of the image will be the most stable, and perform the appropriate filtering so that the input of the algorithm is not intensity, but this characteristic.

Practice

Let's try out in practice the algorithms that we offer OpenCV.

Here you can do a lot of different studies of each algorithm, varying parameters, changing input sequences — with different shifts, rotations, projective transformations, segments, with different noises, etc. It would all take a lot of time and exceed the size of the report in this report, therefore, I propose here to limit ourselves to the simple case of a parallel shift of the image at a fixed distance and the imposition of small noises. This will make it possible to understand in general terms how to run the algorithms and which of them is cooler.

The detailed syntax of the procedures is described on the page with the manual , here I will give a squeeze-translation with my comments.

Classic Lucas-Canada is implemented with a pyramid in the calcOpticalFlowPyrLK procedure. The algorithm calculates the sparse stream, that is, for a given set of points on the first image, estimates their position on the second. The input parameters are fairly obvious: two input images, an input and output point set, status — an output vector that indicates whether the corresponding point was found successfully, err — an output vector of the estimated errors of the corresponding points, WinSize — the size of the window over which Gaussian averaging occurs, I took 21x21 and worked well, maxLevel - the number of layers in the pyramid minus one, that is, the number of the last layer, I took 5, criteria - the condition for exiting the iterative process of determining the shift (minimizing the error is performed iteratively) - this parameter I left default, flags - additional flags may be used such as initial approximation of the flow or to select the method of error estimation, minEigThreshold - gradient threshold, below which is considered a degenerate matrix, I left by default. Starting with OpenCV 2.4.1, you can use a pre-computed pyramid of scaled images when calculating a stream.

The result of the work is that both small and large shifts are successfully and stably detected, resistant to rather large noises, the operating time is about 10 ms for 400 points with a 5-layer pyramid (on core i7 950).

By the way, this algorithm is also implemented on Gpu (CUDA), with both the dense and sparse versions.

The Farneback stream is implemented by the calcOpticalFlowFarneback procedure, a dense stream is calculated, that is, the shift of each point. Parameters: input images, output stream in the format of a dual-channel matrix of floats, pyr_scale determines the ratio of scales between the layers of the pyramid, levels - the number of levels in the pyramid, winsize - the size of the window over which the averaging is performed, iterations - the number of iterations at each level, poly_n - the size of the polynomial by which the values ​​of A and b are evaluated, poly_sigma - sigma of the Gaussian blur when smoothing derivatives, the recommended values ​​of parameters are indicated in the manual, flags - additional flags, for example, you can use the initial approximation ix flow or otherwise averaged over the window.

This algorithm is much less stable (according to my observations), it is easier to miss in fairly uniform pictures (apparently, the problem is in the absence of filtering of unsuccessful points), it is poorly defined by large shifts. I worked for 600 ms on the image 512x512.

The SimpleFlow stream is implemented by the calcOpticalFlowSF procedure (again, a dense stream is calculated), and it has many mysterious parameters without default values, and in general at the moment the information on the page is presented very succinctly. Let's try to figure it out. The first 3 are input images and two-channel output; layers - the number of layers in the pyramid, that is, how many times the original image is scaled; averaging_block_size - the size of the window in which we considered the pixel energy function; max_flow is the maximum shift that we want to be able to determine at each step; in fact, it is determined by the size of the window (although it is not entirely clear why it is int). You can stop at this, or you can set a few more parameters; the meaning of some of them eludes me.

The site offers a look at an example of its use, in which it runs with the following parameters: calcOpticalFlowSF (frame1, frame2, flow, 3, 2, 4, 4.1, 25.5, 18, 55.0, 25.5, 0.35, 18, 55.0, 25.5, 10) ;

My algorithm works much slower than others, about 9-12 seconds per 512x512 image. The result of the work seems to be more believable than Farneback, at least the shift in uniform pictures is better defined, it works much better with large shifts.

findings

If you want to use an optical stream somewhere, first think about whether you need it: you can often do with simpler methods. It’s worthwhile to realize the stream independently only a few times after thinking: each algorithm has a lot of tricks, subtleties and optimizations; , , OpenCV (, , ). SSE , , CUDA OpenCL . . (. . sparse ), calcOpticalFlowPyrLK, , . dense- calcOpticalFlowSF, . , calcOpticalFlowFarneback, , .

Literature

docs.opencv.org/modules/video/doc/motion_analysis_and_object_tracking.html
Pyramidal Implementation of the Lucas Kanade Feature Tracker. Description of the algorithm — Jean-Yves Bouguet
Two-Frame Motion Estimation Based on Polynomial Expansion — Gunnar Farneback
SimpleFlow: A Non-iterative, Sublinear Optical Flow Algorithm — Michael Tao, Jiamin Bai, Pushmeet Kohli, and Sylvain Paris
Horn-Schunck Optical Flow with a Multi-Scale Strategy — Enric Meinhardt-Llopis, Javier Sanchez
en.wikipedia.org/wiki/Optical_flow