The problem of monkeys and infinity
Everyone knows that if you plant a monkey for a typewriter and make it always accidentally knock on the keys, then sooner or later, it will type “War and Peace”, a collection of Pythagorean works and even the article you are reading now.

A terrific fact, but it is even more interesting to try to understand how much time it will take to type a particular text. In order not to drive an extra parameter - the speed of a monkey set - we will look for the answer to the question: how many keystrokes will it need on average. Is it obvious to you that the string “abc” is much easier to type than “aaa”? This post is dedicated to solving this problem. Along the way, the prefix function and its properties are explained.
It is clear that the time spent by the monkey on typing a specific text is a certain random variable. Therefore, it is logical to ask about her expectation.
Formal statement of the problem
A string s is given, consisting of uppercase Latin letters („a“ - „z“). Need to find a mat. waiting for the number of random keystrokes before the entire string s is typed, if all characters are typed equiprobably (with a probability of 1/26 ).
To understand why this works and what the Pi () function is, you need to read the whole article :(.
string s; //, int n = s.length(); vector<int> p = Pi(s); vector<long double> pow(n+1); pow[0] = 1; int i; for (i = 1; i <= n; i++) { pow[i] = pow[i-1]*26; } long double ans = 0; for (i = n; i>0; i = p[i-1]) { ans += pow[i]; } cout << ans; Prefix function
This function will help us to solve the problem. The prefix function was introduced by D. Knuth and M. Pratt (and in parallel with D. Morris) for their famous substring search algorithm in the string ( ILC algorithm). The prefix function for string s returns the length of the longest proper prefix of the string, which is also its suffix.
The prefix is just the beginning of the line, if you drop some characters from the end. So the string "aba" has 4 prefixes: "" (empty string), "a", "ab" and "aba". The suffix is the same, but the characters are removed from the beginning. However, some suffixes and prefixes may coincide. For the string "aba" there are 3 such prefix-suffixes: "", "a" and "aba" (the fourth suffix "ba" does not match the prefix "ab"). The suffix or prefix is called proper if it is shorter than the entire string.
Formally speaking:
Where pref k (s) is a prefix of length k of string s , and suf k (s) is a suffix of length k of string s .
As in the KMP algorithm, and in other applications, it is much more useful to consider the prefix function for all prefixes of a given string at once. Yes, it sounds scary - for each prefix you need to find the largest of your own prefix, which coincides with the prefix suffix. But in fact, everything is simple:
Such an extended prefix function is useful primarily because it is easier to calculate than just . The following values are shown.
for s = "ababac".
k: 1 2 3 4 5 6
s: ababac
P (i): 0 0 1 2 3 0 Calculation function prefix
vector<int> Pi(string s) { int n = s.length(); vector<int> p(n); p[0] = 0; for (int i = 1; i < n; i++) { int j = p[i-1]; while (j > 0 && s[i] != s[j]) { j = p[j]; } if (s[i] == s[j]) j++; p[i] = j; } return p; } Fast, beyond O (N) , the calculation of the function prefix is based on two simple observations.
(1) To get the prefix suffix for position k, you need to take some kind of prefix suffix for position k-1 and append the character at position k to the end of it.
(2) All prefixes-suffixes of string s of length n can be obtained as and so on, until the next value is equal to 0. This property can be checked on the string "abacaba". Here
that matches all suffix prefixes ("aba", "a" and ""). This is because the maximum prefix suffix has a length
. The next in length prefix suffix will be shorter. But since the first prefix suffix occurs both at the beginning and at the end of the string s , the next prefix suffix will be the longest prefix suffix in the first prefix suffix.
Therefore, to build the function prefix for position i, it is sufficient to iterate from the function prefix value in the previous position until the extension of the suffix with the new character is also a prefix (for this you need to check only one new character). Such an algorithm is executed in linear time, because the value of the function prefix increases by a maximum of 1 each time, so it cannot be reduced more than n times, which means that the nested loop will be executed in total not more than n times.
KMP Machine
The following mathematical object, which is necessary in solving the set task, is a finite state machine that accepts lines ending in a given string s . This machine is used in another, less well-known modification of the Knut-Moriss-Pratt algorithm. In this version of the algorithm, a finite state machine is constructed that accepts all strings that end with a given string (pattern). Then the string is passed to the machine. Every time the machine accepts the text transmitted to it, the next occurrence of the pattern is found. It is this machine that will help us solve the monkey typing machine problem.
A finite state machine is a mathematical object that is easiest to imagine as some kind of box that has some kind of internal state. Initially, the box is in the initial state . You can enter lines in the box, one character at a time. After each character, the box changes its state, depending on the current state and the character entered. Also, some states are good (the mathematical term is final states ). It is said that the automaton accepts the line , if after feeding this line with a symbol-by-character, the automaton is in good condition.
To determine the QA, you need to determine the initial state, good states and the transition function - for each state and symbol you need to specify a new state to which the machine will go. It is convenient to draw an automaton as a full directed graph, where vertices are states, and exactly one character is written on each edge. From each vertex there must be exactly one edge with each symbol. Then, to process a string, you just need to go over the edges with the characters from this string. If the path ended in the final state, then the machine accepts such a string.
To build this automaton, we will use the prefix function already known to us.
The automaton will have n + 1 state, numbered from 0 to n . The state k corresponds to the coincidence of the last k characters typed with the prefix of the pattern of length k (If we search for the string "abac", then we are interested in the current text just at the end: "abac", "aba", "ab", "a" or what something else. This information is enough to get the same after writing one character). State 0 will be initial and state n will be final. Sometimes there can be confusion: for example, for the terms “ababccc” with the zzzabab line fed to the automat, you can choose both state 2 and 4. But in order not to lose the necessary information about the typed text, we will always choose the greatest state.
Here is the automaton for the string "ababac". For example, the alphabet consists only of the characters 'a' - 'c'. Parallel ribs are combined for clarity. In fact, only one symbol corresponds to each edge. The initial state is 0 , the final state is 6 .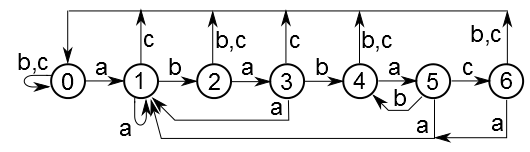
It is easy to make sure that any path from state 0 to state 6 , no matter how difficult it is, necessarily ends with the string "ababac". Conversely, any such path will necessarily end in state 6 .
string s; // . int n = s.length(); vector< vector<int> > nxt(n+1, vector<int>(256)); // nxt[][] == vector<int> p = Pi(s); // . . nxt[0][s[0]] = 1; // 0 0. for (int i = 1; i <= n; i++) { for (int c = 0; c < 256; c++) nxt[i][c] = nxt[p[i-1]][c]; //p[] , -1 if (i < n) nxt[i][s[i]] = i+1; } Notice how the transitions are constructed. To calculate transitions from state i, we consider 2 options. If the new symbol is s [i], then the transition will be to the state i + 1 . Everything is obvious here: if there was a match in i characters, then by adding the next character from string s, we will increase the length of the match by 1 . If the symbol does not match, then we simply copy the transitions from the state . Why? The transition in this case will be exactly in the state with the number ≤i . So after the transition, we will forget some of the information about the typed text. You can do this before proceeding. The very minimum that we can erase is to pretend that in reality the state now is not i , but
. It is like in the example above, it was possible to consider that the text ends with “abab” or “ab”. If there are no transitions from abab, you can use transitions from ab.
Decision
Now we are ready to solve the task.
Construct for the string s an automaton KMP. Since all characters are typed by a monkey randomly, the characters themselves are not important to us, but only the edges in the transition graph. The problem can be reformulated as follows: find mat. waiting for the number of transitions in a random walk from state 0 until state n is reached.
It is logical in this formulation to introduce variables: E k , 0≤k≤n is the expectation of the number of transitions to reach state n . E 0 will be the answer to the original problem. Let Z be the set of valid characters (the alphabet). You can create a system of equations:
Equation (1) means that when reaching state n, random walk stops.
For any other state, some kind of transition will be made, therefore the term 1 is present in equation (2). The second term is the sum of all possible variants multiplied by the probability of these variants. All probabilities are the same - therefore it is taken out for the sum sign.
There is already a solution to the problem in O (n ^ 3): the constructed system of linear equations can be solved by the Gauss method. But if you look at this system a little and remember that there is a prefix function, that is, the solution is much simpler and faster.
Recall the construction of a finite automaton. (For simplicity, instead of i will use just
). Transitions from state k almost completely coincide with transitions from state
. The difference in the transition only by the symbol s [k-1]. Therefore, the right sides of equations (2) for the states k and
differ only in one term. In the equation for
worth
instead
in the equation for k . Moreover, nxt [k] [s [k-1]] = k + 1 . Using this fact, you can rewrite equations (2):
Now we need to make another observation. Turns
Those. to find the prefix function for a certain state, one must take the prefix function from the previous state and go from there to the symbol leading to the next state.
Indeed, if we consider the state , then it corresponds to a string ending in the character s [k-1]. So there is a transition to this symbol. Consider the largest state from which such a transition exists, but which has the number <k . If, after moving on the symbol s [k-1], we got some kind of suffix
then before the transition it was a suffix
. Since this was the rightmost such state, it corresponds to the maximum prefix-suffix
which means it has a number
. So we got this amazing and useful fact.
Then (3) is converted to:
Or in another way:
On both sides of the equals sign there are negative numbers (it is logical that the larger the k , the smaller E k ). Multiply both sides by -1 .
But (4) is valid only for k> 0 . For k = 0, one can explicitly write out equation (2), because only one of | Z | transitions leads to state 1 , and all the others return to state 0 :
Now we collect all the variables on the left, multiply the equation by | Z | and replace (the prefix function for one character is always 0, because one character does not have non-empty proper prefixes):
I allow myself to repeat equations (1), (4) and (5), since they constitute a system that we will now solve analytically:
Substituting the first equation into the left side of the second with k = 1 , then with k = 2 , etc. we get:
Now the solution is almost ready: now consider (6) with k = n and recall that we get:
Substitute this value in (6) with - we get:
Similarly, we get:
And so you can continue as long as we do not get the expression for which, by the way, is the answer to the problem. Denote
function applied k times in a row
, then:
Thus, we have obtained the solution of the problem in O (n): construct the prefix function to the string s and iterate over it starting from n until we reach 0 , adding the powers of | Z | equal to the current prefix length. This is the very solution given at the beginning of the article.
Looking at (*) it becomes clear why the string “aaa” is harder to type than “abc”, because in aaa there is only the third iteration is zero, and the second line has no non-empty prefixes equal to the suffixes and
immediately gives zero.
Remarks
The prefix function and the KMP automaton are very useful tools for working with strings. If dear readers have an interest, then I can make out solutions to other problems. Any typos please report in a personal, thank you.
Update:
Firstly, thanks a lot to parpalak for its great service for preparing articles with formulas on Habré ( https://habrahabr.ru/post/264709/ ). Without him, this article would not exist. I am very ashamed that I forgot to write about it right away.
Secondly, very many commentators are confused by their intuition. In teorvere this often happens. Yes, the probabilities of typing texts of the same length from the first time are the same. Yes, the frequency of occurrence of the same length texts is the same in an infinite random text. All this is true, but it does not follow from these facts that the expectation of the number of characters before the first occurrence of the lines will be the same. And vice versa, from the fact that the string “hh” in the endless text will occur later than the string “chk” it does not follow that in the casino it is necessary to put red after the black.
Let's calculate the expectation on the fingers until the two lines “hh” and “chk” are drawn. The expectation is the sum over all i : the probability of typing a string for i characters for the first time multiplied by i . The phrase in bold means that, firstly, the last characters typed coincide with the required ones (this probability is the same for both lines), and, secondly, the required line is not found among the first i-2 characters. This second multiplier is different for different lines. The probability of not finding a line is simply the number of all texts in which this line is not divided by the number of all texts of that length.
Now important: lines of length k not containing the string “chk” of all k + 1 : “k ... k”, “k… kch”, “k… kchch”, “k… kkkchch”, ..., “kch ... h” and “ h ... h. " This is because after the “h” character there can only be “h”.
The sink of the length k not containing the string “hh” will be much larger, namely F k + 1 - the Fibonacci number under the number k + 1 (these are the numbers 1, 1, 2, 3, 5, 8, 13, ... - each next is the sum of the previous two). For example, for k = 2 3 lines will be "kk", "kch", "chk". These numbers are growing very quickly and therefore all the terms for the checkmate for the string "QC" will be greater, since there is more likelihood.
Please note, all due to the fact that the likelihood to print text for the first time in a few clicks depends on the probability not to print the text even at the beginning and middle of the text. This probability is directly proportional to the number of rows that do not contain the specified string, but it is different for different patterns.
Once again, it was not I who invented it, it is a well-known fact, although it is extremely unintuitive. Look, for example, at this article (look for a task about Alice and Bob there - paragraph 4): https://habrahabr.ru/post/279337/
')
Source: https://habr.com/ru/post/200834/
All Articles