Tower of Hanoi on the fingers

After talking with some familiar programmers, I suddenly discovered that not everyone knows about the Tower of Hanoi, and among those who know, very few understand how this problem is solved.
Wikipedia writes about this very strictly, in the case, and does not explain anything. Like, take it as a truism. Therefore, to understand how it is solved is difficult at once. But the problem is very simple, and yet interesting in programming and mathematically.

The article will be a lot of pictures. Explanation of how to solve a problem recursively and how it is solved by binary search.
In general, the article is dedicated to those brave people who are still afraid of the Tower of Hanoi, but want to stop being afraid of it.

Rules of the game

They are very simple. There are 1 pyramid with disks of different sizes, and 2 more empty pyramids. It is necessary to move the disks from one pyramid to another. You can only shift one disk per turn. It is possible to fold the disks only smaller for larger.
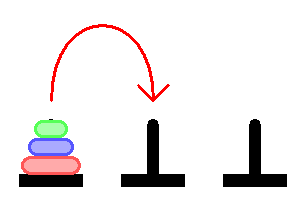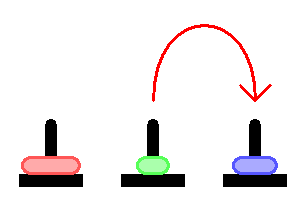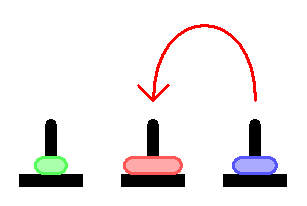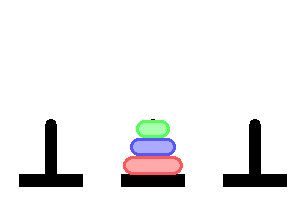
So here we have this pyramid:

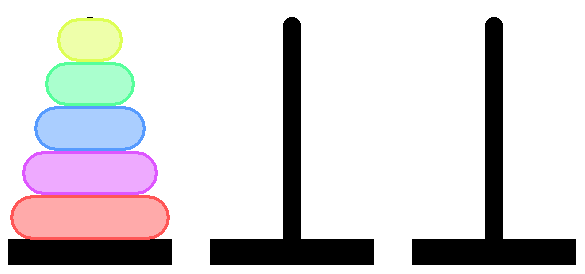
And we need to shift it to say the middle axis.
If you start solving a problem not from the beginning, but from the end - it turns out to be very simple. Let's think about it. To shift the pyramid to the second axis - we need to shift the lowest disk, and this can be done only when the 4 upper disks are on the third axis:

In order to shift the 4 disks to the third axis, you need essentially to solve the same problem, but for 4 disks. That is, we can shift the 4th disk to the third axis only when we have 3 disks on the second axis:

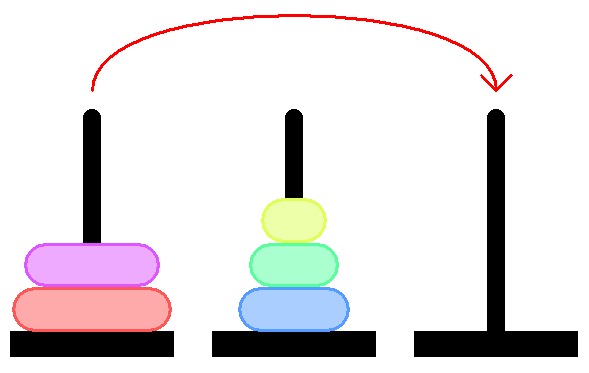
Feel recursion?
Moving the stack of 5 disks is:
1. Shifting the stack from 4 disks to an independent axis
2. Shifting the 5th disk to the axis we need
3. Shifting the stack of 4 disks to the axis we need

In turn, shifting the stack of 4 disks is:
1. Shifting the stack from 3 disks to an independent axis
2. Shifting the 4th disc to the axis we need
3. Shifting the stack from 3 disks to the axis we need
')
That's all.

Recursive implementation

After such a detailed description will not be difficult to implement it algorithmically.

Algorithmic complexity

We can easily calculate how many actions we need to move the pyramid.
If we move the stack from one disk, then we need 1 action.
If the stack of two is 1 * 2 (move the stack from one disk twice) + 1 (move the last disk)
If out of three ((1 * 2) + 1) * 2 + 1
Of the five: ((((((1 * 2) + 1) * 2 + 1) * 2 + 1) * 2 + 1)
So each operation increases by 2 times + 1 number of movements. Expanding the brackets for n operations, we get:

You can get rid of the amount, because it is equal to:

ps I got rid of the amount in my head, remembering the sum of the members of an infinitely decreasing geometric progression, but I hope the mathematicians will show how to correctly write these transformations
In total, after all the transformations, we have:


That is, if we want something strange, for example, to write down the decision of the tower of Hanoi for 64 discs, then we will not have enough modern media. In fact, we don’t have to write anything down at all. It is like recording all the numbers from 0 to + infinity to use them later, because the solution of the Hanoi Tower is a fractal.

Fractal nature

Yes Yes. The decision of the Hanoi tower has a fractal nature. Let's get a look. Suppose we have every action written in a string. Then for a tower of 6 discs you can write it something like this:

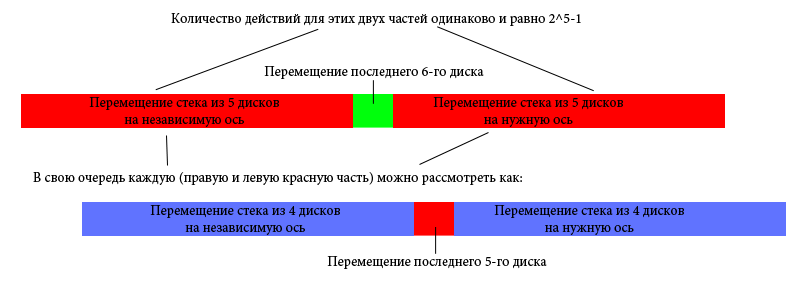
Well, since this is a fractal, we can easily call any operation knowing only its sequence number. And even more, we can exactly restore the position of all disks at the time of any operation.

Binary algorithm

So, we know the exact number of operations, as well as we know the index of the operation for which we want to restore the state.
Suppose we have a tower of 6 disks (we move as usual, from the 1st to the middle axis), which means we have 2 ^ 6-1 = 63 operations. Suppose we need to restore the state for the 49th operation.
Divide the integer 63 by 2. It turns out 31. This is the index of the operation on which the 6th disk will be moved:

We have the 49th operation index. This means that the 6th disk already lies on the middle axis. In addition, since we are in the right part, the fifth disk we have lies either on the 3rd axis, or on the 2nd. In order for us to work with the tower according to the same algorithm - subtract from the 49th operation 32, we find the sub-operation index. This is 17. To move a stack of 5 disks, 31 operations are needed, while the 5th disk is moved to the 16th operation and from the 3rd axis to the 2nd one.
So the number 17 is to the right:

This means that the disk 5 has already been moved to the second axis.
By analogy, we restore the position of the remaining disks.

Implementation (binary method)

I added beautiful turret drawing. Agree, boring to look at the console log. Therefore, the implementation has grown, and I will attach the complete project (source code + binary) at the end of the article. Here I will give

Sierpinski Triangle

I would like to casually mention an interesting feature. If all possible movements of the rings are collected in a graph, then for each node there will most often be 3 links. All nodes and connections can be beautifully arranged in the shape of a triangle. The Sierpinski Triangle:

Read more about it on wikipedia here . That in general is not surprising, because we already know the fractal nature of the solution;)

Total

I tried to show how sometimes it would just seem like an not entirely obvious task. Moreover, with careful study, you can suddenly discover completely different interesting algorithms for solving a problem, opening up new possibilities. Search for different approaches, experiment, analyze. After all, we are programmers.
Thanks to those who read it, and who liked the article. I attach a demo example in which you can go with a trackbar, and see how the turrets are shifted.

Binary algorithm example (exe + source code, Delphi)