We aim from the gun

The article describes a simple gun targeting algorithm, when the axis of rotation does not intersect with the axis of the barrel. It was not possible to quickly find the ready one - I had to remember the school days. Well, since I remembered, it is a sin not to share with the rest. And someone somewhere, saving time, uses it to create something more useful ...

The result of the above calculations is used in an arcade game. For a month there were no misses. If you are developing a simulator, you will most likely need something more sophisticated.


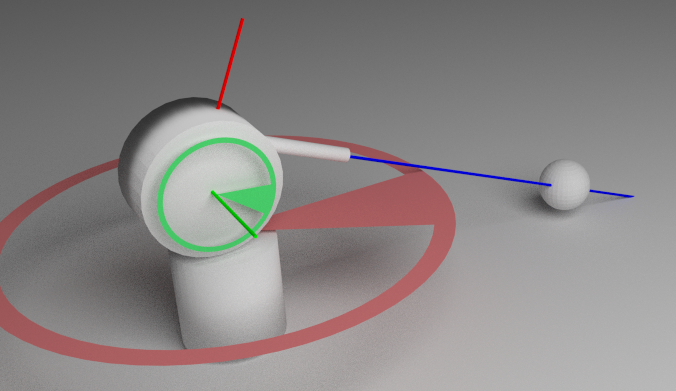
So, given the gun. When hovering, the turret can rotate in the horizontal (red axis of rotation in the figure) and vertical (green axis) planes.
')
Gun Model Properties

1. The stem axis (marked in blue) does not intersect with the axes of rotation.
2. The axis of the trunk is parallel to the axis X
3. The direction of the shot coincides with the positive direction X
4. The horizontal rotation axis (red) is parallel to the Z axis, or the axes coincide.
5. The vertical rotation axis (green) is parallel to the Y axis, or the axes coincide.
6. The top of the model corresponds to the positive direction of the Z axis.

For successful targeting you need to calculate two angles of rotation - horizontal and vertical.



Due to the specified constraints of the model (the axes of turns are parallel or coincide with the corresponding axes of coordinates), the task of finding the pointing angles in three-dimensional space can be divided into two in two-dimensional:

1. The angle of horizontal rotation can be found using the model projection on the XY plane (Z = 0)
2. Angle of vertical rotation - XZ axis (Y = 0)

Solve both subtasks will be the same.

To begin, consider the starting position.



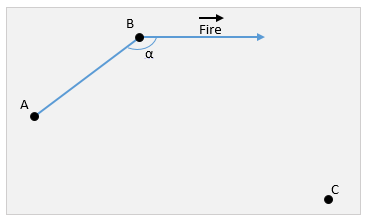
A is the center of rotation. The result of the projection of the axis of rotation on the perpendicular plane.

B - the point of departure of the projectile.

Fire is a projection of the direction vector of the shot.

C - goal position

Determine the angle between the shot vector and AB



Hereinafter, the angular brackets will denote the scalar product of vectors.

Now suppose the guidance is complete. When turning to the target, point B went to D, and the Fire vector became Fire1



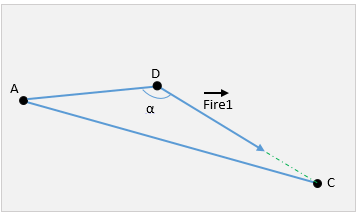
From here you can find the length of the DC segment using the cosine theorem.



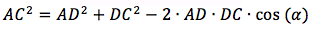
Where





Rewrite the formula to match the general form of the quadratic equation



for unknown DC









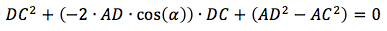
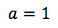
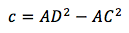
then



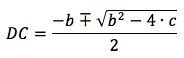
of the two DC values ​​that are obtained, we are positive.

If DC turns negative, then the target is inaccessible (at least using this algorithm) for positioning.

Now consider the figure, which shows the position of the system before and after pointing



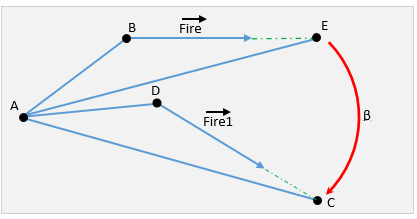
Red indicates the desired angle of guidance.

Determine the coordinate of point E. This is the coordinate of target C, rotated by the aiming angle relative to center A in the opposite direction. Ie this is where the gun would hit if it had fired at the correct distance, forgetting to turn. To do this, shift point B in the direction of the Fire vector to a distance DC.



Then the aiming angle is the angle between the vectors AE and AC, which is through the scalar product



The angle is found, but you need to remember that the aiming point can be anywhere, including “above” the direction of the shot. Those. need to find another direction of rotation.

Determine the orientation of the vectors AE and AC. Two vectors are not enough for this. We need a third vector perpendicular to the first two. Let's call it V. It is his direction that determines the position of the observer, who will see the rotation clockwise or counterclockwise, depending on which side of the plane with the vectors AE and AC is located. Since we are working with projections on coordinate planes, the desired vector will be parallel to the third coordinate axis.

For definiteness, consider an example of a projection on the XY axis. In this case, the perpendicular vector will have coordinates (0, 0, z), where z is not equal to zero. With the z sign you need to decide. When building the projections, I proceeded from the fact that I am on the positive side of the Z axis, therefore z> 0

The orientation of the vectors is determined by the sign of the determinant, composed of coordinates. The first line is the coordinates of the rotated vector, the second is the vector to which the first and the third vectors are rotated. For our case (AE rotates to match AC), this



Since we have determined that z is strictly positive, its value will not affect the sign of the result



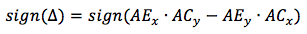
Ie the final angle of rotation for the case of projection on the XY axis, this



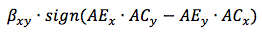
Similarly, the direction of rotation is calculated for the projection on the XZ axis.

Well, the last remark. Fully independent of each other, the angles of rotation can not be calculated. The turret can make a complete turn (from -180 to 180 degrees) around the horizontal axis, but around the vertical this is usually impossible (it will look as if the gun has come off the ground and turned over. Vertical turn is logical to limit to the range from -90 to 90 degrees.

This is the easiest to implement.

1. Find the angle of horizontal rotation
2. Turn the target at this angle around the axis of horizontal rotation in the opposite direction
3. Calculate the vertical angle of guidance for the new coordinates of the target.

Or (which is essentially the same), you can first rotate the tower horizontally, and then calculate the angle of vertical rotation.

Now the gun will fall.