Counts for the smallest: DFS
In this article, I would like to talk about one of the most common algorithms on graphs - about detours in depth - on the example of solving the problem of finding a path through a maze. Anyone who is interested is welcome under the cut!
Working on a “raw” labyrinth is rather inconvenient (at least, the introduction of the graph will be unattractive), so we will break it into “rooms” connected by partitions. Approximately as shown in the figure on the right.
Now the task took the form: there are many rooms, you can move between some of them. It is required to find a way from room A to room B.
In graph theory, “rooms” are called vertices, and “transitions” between them are edges. Room A is the initial peak, Room B is the final one.
The graph in the picture on the right can be redrawn in a slightly more common form in graph theory:
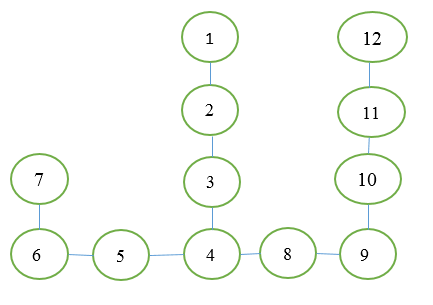
Here, the ovals are the tops (or rooms), the lines are the edges (or transitions between them). Vertex 1 - initial, vertex 12 - final.
The first thing I want to do is write a bust: at each moment of time we are at some peak, and go from it to all the neighbors:
Alas, this code does not work already on a graph of three vertices, in which each vertex is connected to each vertex with edges - when starting from vertex 1 we go to vertex 2, from it to vertex 1, from it again to vertex 2, ... and at some point, the program simply crashes due to a stack overflow.
The solution that immediately comes to mind is to mark each vertex at the entrance to it, and never go to the already marked vertices - this is a detour in depth:
Yes, the program went along some path, but how to determine which path?
For each vertex, we will remember where we came from in the prior array in a special array.
Then the task of restoring the path will be trivial:
The algorithm will always find the way to the top, if it exists. Evidence:
For an arbitrary graph G:
Base. The path from no more than 1 vertex is found by the algorithm (the path from the initial vertex to it is the same).
Assumption: The algorithm visits all vertices that are at a distance no more than k - 1 from the initial one.
Step: Consider any vertex v located at a distance k from the initial one. Obviously, it is connected by an edge with some vertex located at a distance k - 1 from the initial one — let's call it w. So, we will go to the vertex v when viewing the vertex w.
The algorithm scans each edge once, and performs a constant number of actions for each vertex. Denoting the number of vertices as V, and the edges as E, we find that the running time is O (V + E).
The depth of recursion in which we are located does not exceed the total number of calls to the DFS function — the number of vertices. That is, the amount of memory required for the operation of the algorithm is O (V).
Any recursive algorithm can be rewritten in non-recursive form. Here is the code for the DFS:
I hope it was informative. In the following articles I will try to tell more about what tasks can be solved with the help of DFS, as well as why we need BFS, Dijkstra and other algorithms on graphs.
Formulation of the problem
Working on a “raw” labyrinth is rather inconvenient (at least, the introduction of the graph will be unattractive), so we will break it into “rooms” connected by partitions. Approximately as shown in the figure on the right.
Now the task took the form: there are many rooms, you can move between some of them. It is required to find a way from room A to room B.
In graph theory, “rooms” are called vertices, and “transitions” between them are edges. Room A is the initial peak, Room B is the final one.
The graph in the picture on the right can be redrawn in a slightly more common form in graph theory:
Here, the ovals are the tops (or rooms), the lines are the edges (or transitions between them). Vertex 1 - initial, vertex 12 - final.
And how will we solve this problem?
The first thing I want to do is write a bust: at each moment of time we are at some peak, and go from it to all the neighbors:
Bust
It is assumed that the graph is stored in an array of vector <vector <int >> edges, and edges [v] contains the numbers of all the vertices to which there is an edge from v. It also assumes that the number of the final vertex is stored in the global variable finish.
void travel(int v) { if (v == finish) // , { cout << "Hooray! The path was found!\n"; return; } for (int i = 0; i < (int)edges[v].size(); ++i) // { travel(edges[v][i]); // } } Alas, this code does not work already on a graph of three vertices, in which each vertex is connected to each vertex with edges - when starting from vertex 1 we go to vertex 2, from it to vertex 1, from it again to vertex 2, ... and at some point, the program simply crashes due to a stack overflow.
What to do?
The solution that immediately comes to mind is to mark each vertex at the entrance to it, and never go to the already marked vertices - this is a detour in depth:
DFS
void DFS(int v) { if (mark[v] != 0) // , { return; } mark[v] = 1; // , if (v == finish) // , { cout << "Hooray! The path was found!\n"; return; } for (int i = 0; i < (int)edges[v].size(); ++i) // { DFS(edges[v][i]); // } }
So what?
Yes, the program went along some path, but how to determine which path?
For each vertex, we will remember where we came from in the prior array in a special array.
DFS
void DFS(int v, int from) { if (mark[v] != 0) // , { return; } mark[v] = 1; // , prior[v] = from; // , if (v == finish) // , { cout << "Hooray! The path was found!\n"; return; } for (int i = 0; i < (int)edges[v].size(); ++i) // { DFS(edges[v][i], v); // } }
Then the task of restoring the path will be trivial:
get_path
vector<int> get_path() { vector<int> ans; for (int v = finish; v != start; v = prior[v]) // { ans.push_back(v); // } ans.push_back(start); reverse(ans.begin(), ans.end()); // return ans; }
And why does this work?
The algorithm will always find the way to the top, if it exists. Evidence:
For an arbitrary graph G:
Base. The path from no more than 1 vertex is found by the algorithm (the path from the initial vertex to it is the same).
Assumption: The algorithm visits all vertices that are at a distance no more than k - 1 from the initial one.
Step: Consider any vertex v located at a distance k from the initial one. Obviously, it is connected by an edge with some vertex located at a distance k - 1 from the initial one — let's call it w. So, we will go to the vertex v when viewing the vertex w.
How many resources does the algorithm need?
The algorithm scans each edge once, and performs a constant number of actions for each vertex. Denoting the number of vertices as V, and the edges as E, we find that the running time is O (V + E).
The depth of recursion in which we are located does not exceed the total number of calls to the DFS function — the number of vertices. That is, the amount of memory required for the operation of the algorithm is O (V).
Non-recursive DFS
Any recursive algorithm can be rewritten in non-recursive form. Here is the code for the DFS:
DFS
void DFS() { stack<int> s; s.push(start); while (!s.empty()) { int v = s.top(); s.pop(); for (int i = 0; i < edges[v].size(); ++i) { if (mark[edges[v][i]] == 0) { s.push(edges[v][i]); mark[edges[v][i]] = 1; } } } }
What's next?
I hope it was informative. In the following articles I will try to tell more about what tasks can be solved with the help of DFS, as well as why we need BFS, Dijkstra and other algorithms on graphs.
')
Source: https://habr.com/ru/post/200074/
All Articles