Data transfer efficiency and information theory
Coding information in its simplest form originated when people communicate in the form of gesture codes, and later in the form of speech, the essence of which is code words for transmitting our thoughts to the interlocutor, then a new stage in the development of such coding - writing, which allowed storing and transmitting information with minimal loss from the writer to the reader. Hieroglyphs - there is a finite alphabet, denoting concepts, objects or actions, the elements of which, in some form, are predetermined by people for an unambiguous "decoding" of recorded information. The phonetic letter uses an alphabetic alphabet for internal coding of words of speech and also serves for unambiguous reproduction of recorded information. Numbers allow you to use code representation calculations. But these types of coding served rather for direct communication, but people also needed to transmit information over a distance and quickly enough, as a result, the simplest telecommunication systems appeared.
The most important leap in the history of the development of information transfer was the use of digital data transmission systems. The use of analog signals requires a large redundancy of information transmitted in the system, and also has such a significant drawback as the accumulation of interference. Various forms of coding for the conversion of analog signals into digital ones, their storage, transmission, and conversion back to analog form began their rapid development in the second half of the 20th century, and by the beginning of the 21st analog systems were almost crowded out.
The main problem that needs to be solved when building a communication system was first formulated by Claude Shannon in 1948:
Such an accurate and clear statement of the communication problem has had a tremendous impact on the development of communications. There was a new science industry, which became known as the theory of information. The main idea, justified by Shannon, is that reliable communications must be digital, i.e. The communication task should be considered as transmitting binary digits (bits). Now it is possible to unequivocally compare the transmitted and received information.
')
Note that any physical signal transmission channel cannot be absolutely reliable. For example, noise that spoils the channel and introduces errors in the transmitted digital information. Shannon showed that under certain fairly general conditions there is a fundamental possibility of using an unreliable channel for transmitting information with an arbitrarily large degree of reliability. Therefore, there is no need to try to clear the channel of noise, for example, by increasing the power of the signals (this is expensive and often impossible). Instead, efficient coding and decoding schemes for digital signals should be developed.
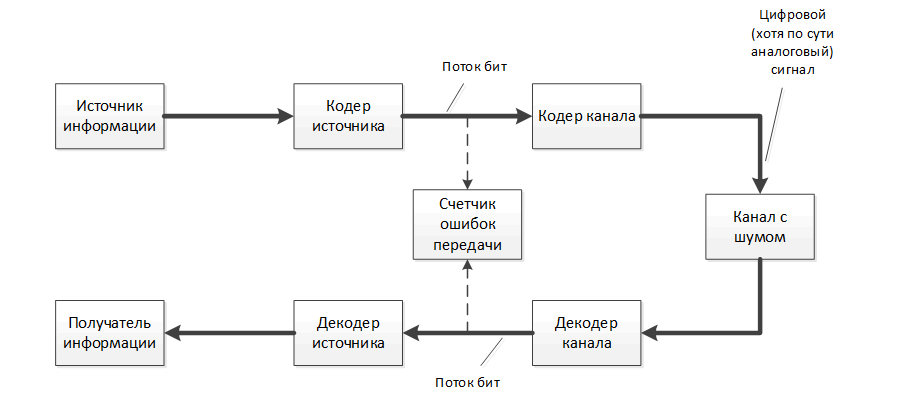
The task of channel coding (selection of the signal-code design) is to build on the basis of known channel characteristics an encoder that sends input symbols to the channel that will be decoded by the receiver with the maximum degree of reliability. This is achieved by adding some additional verification characters to the transmitted digital information. In practice, the channel can be a telephone cable, satellite dish, optical disk, computer memory or something else. The task of source coding is to create a source coder, which produces a compact (shortened) description of the original signal, which must be transmitted to the addressee. The signal source can be a text file, a digital image, digitized music or a television program. This concise description of the source signals may be inaccurate, then you should talk about the discrepancy between the restored after receiving and decoding the signal and its original. This usually occurs when converting (quantizing) an analog signal to digital form.
Direct theorem:
Inverse theorem:
For additive white Gaussian noise, Shannon obtained the following expression:
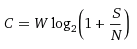where
C - channel bandwidth, bit / s;
W - channel bandwidth, Hz;
S - signal power, W;
N - noise power, watts.
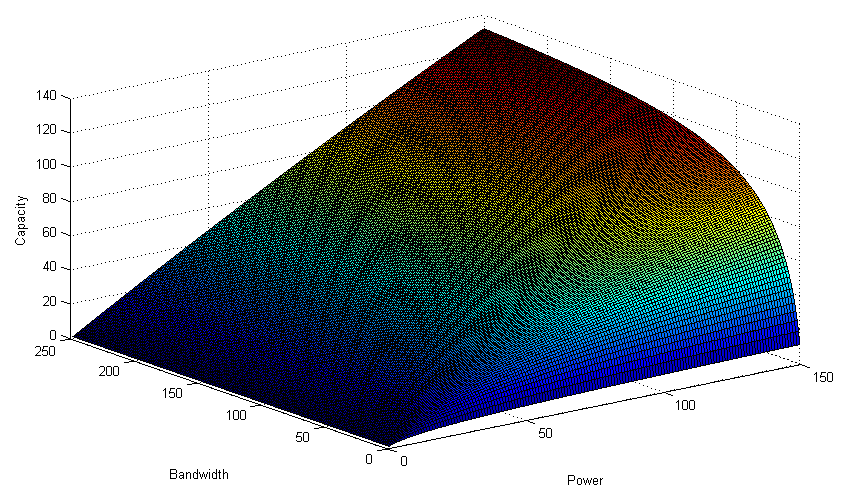
(Graph for clarity, the dependence C (W, P) with N 0 = const; values ​​from the ceiling, I ask you not to look at them)
Since ABGSh power grows linearly with the channel bandwidth, we have that the channel capacity has a limit of C max = (S / N 0 ) log (2), with an infinitely wide frequency band (which grows linearly in power).
where
η - spectrum efficiency, bit / s / Hz;
T R - information transfer rate, bit / s;
W - channel bandwidth, Hz.
Then,
using the energy value of a bit (for signals with complex signal-code constructions, I understand the average energy value per bit) and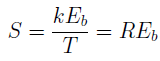 
where
k is the number of bits per character transmitted to the channel;
T - symbol duration, s;
R is the transmission rate in the channel, bits / s;
E b - energy to transmit one bit in the channel;
N 0 is the spectral density of the noise power, W / Hz;
will get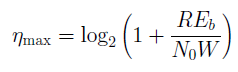
or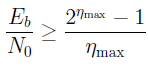 
.
Shannon's limit will be:
This limit makes sense for channels without codecs (R = T R ); to achieve such efficiency, the received word must be infinite length. For channels using noise-tolerant coding codecs, E b should be understood as the energy for transmitting one information bit rather than the channel bit (different interpretations are possible here and I am ready to listen to alternative versions) => E b / N 0 in the channel is different from this value depending on the speed code (1/2, 3/4, 7/8 ...)
Thus, we see that there is a limit of the signal-to-noise ratio in the channel (E b / N 0 ) such that it is impossible to build a data transmission system in which an arbitrarily small error probability can be achieved with a higher noise level (there may be a system with just a small probability of error, with a limiting attitude!).
R. Gallager "Information Theory and Reliable Communication" - M .: "Soviet Radio", 1974.
Salomon D. “Compression of data, images and sound” - M .: Tekhnosfera, 2004
Thank you for your attention, as a continuation, if you're interested, I can write an article with illustrations and a comparison of the effectiveness of signal-code constructions in relation to the Shannon border.
The most important leap in the history of the development of information transfer was the use of digital data transmission systems. The use of analog signals requires a large redundancy of information transmitted in the system, and also has such a significant drawback as the accumulation of interference. Various forms of coding for the conversion of analog signals into digital ones, their storage, transmission, and conversion back to analog form began their rapid development in the second half of the 20th century, and by the beginning of the 21st analog systems were almost crowded out.
The main problem that needs to be solved when building a communication system was first formulated by Claude Shannon in 1948:
The main property of a communication system is that it should accurately or approximately reproduce at a certain point in space and time some message selected at another point. Usually, this message has some meaning, but it is not at all important for solving the engineering problem. The most important thing is that the message being sent is selected from a certain family of possible messages.
Such an accurate and clear statement of the communication problem has had a tremendous impact on the development of communications. There was a new science industry, which became known as the theory of information. The main idea, justified by Shannon, is that reliable communications must be digital, i.e. The communication task should be considered as transmitting binary digits (bits). Now it is possible to unequivocally compare the transmitted and received information.
')
Note that any physical signal transmission channel cannot be absolutely reliable. For example, noise that spoils the channel and introduces errors in the transmitted digital information. Shannon showed that under certain fairly general conditions there is a fundamental possibility of using an unreliable channel for transmitting information with an arbitrarily large degree of reliability. Therefore, there is no need to try to clear the channel of noise, for example, by increasing the power of the signals (this is expensive and often impossible). Instead, efficient coding and decoding schemes for digital signals should be developed.
The task of channel coding (selection of the signal-code design) is to build on the basis of known channel characteristics an encoder that sends input symbols to the channel that will be decoded by the receiver with the maximum degree of reliability. This is achieved by adding some additional verification characters to the transmitted digital information. In practice, the channel can be a telephone cable, satellite dish, optical disk, computer memory or something else. The task of source coding is to create a source coder, which produces a compact (shortened) description of the original signal, which must be transmitted to the addressee. The signal source can be a text file, a digital image, digitized music or a television program. This concise description of the source signals may be inaccurate, then you should talk about the discrepancy between the restored after receiving and decoding the signal and its original. This usually occurs when converting (quantizing) an analog signal to digital form.
Direct theorem:
If the message transfer rate is less than the communication channel capacity, then there are codes and decoding methods such that the average and maximum decoding error probabilities tend to zero when the block length tends to infinity
In other words: For a channel with interference, you can always find a coding system in which messages will be transmitted with an arbitrarily high degree of fidelity, unless the performance of the source exceeds the capacity of the channel.
Inverse theorem:
If the transmission rate is greater than the capacity, that is, then there are no transmission methods where the probability of error tends to zero with increasing length of the transmitted block.Wiki
For additive white Gaussian noise, Shannon obtained the following expression:
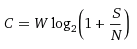whereC - channel bandwidth, bit / s;
W - channel bandwidth, Hz;
S - signal power, W;
N - noise power, watts.
(Graph for clarity, the dependence C (W, P) with N 0 = const; values ​​from the ceiling, I ask you not to look at them)
Since ABGSh power grows linearly with the channel bandwidth, we have that the channel capacity has a limit of C max = (S / N 0 ) log (2), with an infinitely wide frequency band (which grows linearly in power).
whereη - spectrum efficiency, bit / s / Hz;
T R - information transfer rate, bit / s;
W - channel bandwidth, Hz.
Then,
using the energy value of a bit (for signals with complex signal-code constructions, I understand the average energy value per bit) and 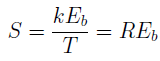wherek is the number of bits per character transmitted to the channel;
T - symbol duration, s;
R is the transmission rate in the channel, bits / s;
E b - energy to transmit one bit in the channel;
N 0 is the spectral density of the noise power, W / Hz;
will get
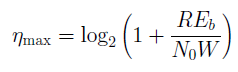or 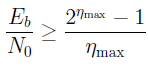.Shannon's limit will be:
This limit makes sense for channels without codecs (R = T R ); to achieve such efficiency, the received word must be infinite length. For channels using noise-tolerant coding codecs, E b should be understood as the energy for transmitting one information bit rather than the channel bit (different interpretations are possible here and I am ready to listen to alternative versions) => E b / N 0 in the channel is different from this value depending on the speed code (1/2, 3/4, 7/8 ...)
Thus, we see that there is a limit of the signal-to-noise ratio in the channel (E b / N 0 ) such that it is impossible to build a data transmission system in which an arbitrarily small error probability can be achieved with a higher noise level (there may be a system with just a small probability of error, with a limiting attitude!).
Literature
R. Gallager "Information Theory and Reliable Communication" - M .: "Soviet Radio", 1974.
Salomon D. “Compression of data, images and sound” - M .: Tekhnosfera, 2004
Thank you for your attention, as a continuation, if you're interested, I can write an article with illustrations and a comparison of the effectiveness of signal-code constructions in relation to the Shannon border.
Source: https://habr.com/ru/post/199488/
All Articles