Optimization optimization in MatLab: nested and anonymous functions
Good day!
I do research in control systems, and Matlab is my main work tool. One of the possibilities in MatLab is numerical optimization. You can optimize (minimize) any function that accepts a vector of variable parameters and returns the value of the criterion to be minimized. Naturally, in the optimization process, the objective function is called many times and its speed is significant. In the lab there are good software tools that often allow you to significantly improve speed, while maintaining readability and ease of maintenance code. I will give an example of the task, show it what anonymous functions and nested functions are, and then show how you can combine these two tools for a noticeable increase in speed.
I have been thinking about the example for optimization for a long time, trying to choose something realistic - finding the optimal trajectory for the kinematically redundant manipulator, approximation of experimental data, identification of parameters. But all this somehow led away from the essence, so I decided to stop at an impractical, but illustrative example. So, given the parameters a and b . It is necessary to find x in the range [0; 1], which maximizes the criterion:
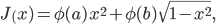
Where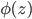 - some function that does not depend explicitly on x , but is necessary to calculate the criterion. Let it be the modulus of the sum of the first million pseudo-random numbers obtained by setting the seed to z . We write a matlab function that calculates the criterion value:
- some function that does not depend explicitly on x , but is necessary to calculate the criterion. Let it be the modulus of the sum of the first million pseudo-random numbers obtained by setting the seed to z . We write a matlab function that calculates the criterion value:
Please note that we return the value with a minus sign, since we want to find the maximum, and the optimization is looking for a minimum.
Now, for optimization with specific values of a and b, we need to make an anonymous function. This is done like this:
Now the
The function
Let's see how this can be optimized. Obviously, every time we call the
and here is the code:
Of course, this is considered much faster. Optimization takes place, on average, in 0.8 ms. But the price for this is code degradation. The integrity of the functional is
It is good that the matlab has a way around this situation. To do this, let's create a nested function inside the
Nested function
')
And now the most interesting - matlab can work with anonymous nested function. Instead of a specific value, our
Now, the handle of the function is written into the returned variable
And this optimization is performed in 0.8 ms.
Result
We obtained the same speed as with the explicit transfer of calculations in the example with
In the future, if you intend to use the function both for optimization and just for computing, then you can add one optional parameter flag to it. If it is not specified, the function returns a value. If set, the handle to the nested function is returned.
I do research in control systems, and Matlab is my main work tool. One of the possibilities in MatLab is numerical optimization. You can optimize (minimize) any function that accepts a vector of variable parameters and returns the value of the criterion to be minimized. Naturally, in the optimization process, the objective function is called many times and its speed is significant. In the lab there are good software tools that often allow you to significantly improve speed, while maintaining readability and ease of maintenance code. I will give an example of the task, show it what anonymous functions and nested functions are, and then show how you can combine these two tools for a noticeable increase in speed.
Problem statement and optimization
I have been thinking about the example for optimization for a long time, trying to choose something realistic - finding the optimal trajectory for the kinematically redundant manipulator, approximation of experimental data, identification of parameters. But all this somehow led away from the essence, so I decided to stop at an impractical, but illustrative example. So, given the parameters a and b . It is necessary to find x in the range [0; 1], which maximizes the criterion:
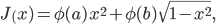
Where
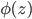 - some function that does not depend explicitly on x , but is necessary to calculate the criterion. Let it be the modulus of the sum of the first million pseudo-random numbers obtained by setting the seed to z . We write a matlab function that calculates the criterion value:
- some function that does not depend explicitly on x , but is necessary to calculate the criterion. Let it be the modulus of the sum of the first million pseudo-random numbers obtained by setting the seed to z . We write a matlab function that calculates the criterion value:function J = GetJ(a,b,x) randn('seed',a); phi_a=abs(sum(randn(1,1e6))); randn('seed',b); phi_b=abs(sum(randn(1,1e6))); J=-(phi_a*x^2+phi_b*sqrt(1-x^2)); end Please note that we return the value with a minus sign, since we want to find the maximum, and the optimization is looking for a minimum.
Now, for optimization with specific values of a and b, we need to make an anonymous function. This is done like this:
a=121233; b=31235; fhnd_GetJ = @(x) GetJ(a,b,x); Now the
fhnd_GetJ variable contains an anonymous function handle that takes one parameter and allows you to calculate GetJ(a,b, ) for the values of a and b specified when creating this anonymous function. You can go directly to the minimization. Let's say we want to find the optimal value of x with an accuracy of 1 millionth: opt=optimset('TolX',1e-6); optimal_x=fminbnd(fhnd_GetJ,0,1,opt); The function
fminbnd(fun,x_min,x_max) minimizes the scalar function of the scalar argument on the interval [ x_min ; x_max ]. Here fun is the handle of the function being optimized. When performing the optimization, the GetJ function GetJ called 12 times; this can be seen by setting the 'Display' parameter in the options as 'iter' - it will show all iterations. On my computer, optimization takes, on average, 10 ms.Increase speed
Let's see how this can be optimized. Obviously, every time we call the
GetJ function GetJ we are completely wasting the values of phi_a and phi_b , since they do not change with the variation of x and depend only on the given values of a and b . How can you save? The most frequent variant that occurs to me is to make preliminary calculations from the objective function. Do this function function J = GetJ2(phi_a,phi_b,x) J=-(phi_a*x^2+phi_b*sqrt(1-x^2)); end and here is the code:
randn('seed',a); phi_a=abs(sum(randn(1,1e6))); randn('seed',b); phi_b=abs(sum(randn(1,1e6))); fhnd_GetJ2 = @(x) GetJ2(phi_a,phi_b,x); optimal_x=fminbnd(fhnd_GetJ2,0,1,opt); Of course, this is considered much faster. Optimization takes place, on average, in 0.8 ms. But the price for this is code degradation. The integrity of the functional is
phi_a - the calculation of phi_a and phi_b has no independent value and is not necessary apart from the calculation of J. If somewhere in another place again you need to consider J (a, b, x) , no longer for optimization, but just like that, then instead of just calling GetJ , you also have to drag the calculation of phi_a and phi_b or do functions for optimization separately, separately for calculations. Well, just not very beautiful.It is good that the matlab has a way around this situation. To do this, let's create a nested function inside the
GetJ function: function J = GetJ3(a,b,x) randn('seed',a); phi_a=abs(sum(randn(1,1e6))); randn('seed',b); phi_b=abs(sum(randn(1,1e6))); J=nf_GetJ(x); function out_val = nf_GetJ(x) out_val=-(phi_a*x^2+phi_b*sqrt(1-x^2)); end end Nested function
nf_GetJ sees all the variables in the scope of the parent function and, in principle, it is clear what and how it does. So far, we have not received any gain in speed - all the same 10 ms for optimization.')
And now the most interesting - matlab can work with anonymous nested function. Instead of a specific value, our
GetJ function can return a handle to its own nested function. And when calling a function on this handle, the parent function will not be executed, but its scope with the parameters counted will remain! We write: function fhnd_J = GetJ4(a,b,x) randn('seed',a); phi_a=abs(sum(randn(1,1e6))); randn('seed',b); phi_b=abs(sum(randn(1,1e6))); fhnd_J=@(x) nf_GetJ(x); function out_val = nf_GetJ(x) out_val=-(phi_a*x^2+phi_b*sqrt(1-x^2)); end end Now, the handle of the function is written into the returned variable
fhnd_J , which allows to calculate the J value for the used parameters a and b , without calculating the phi_a and phi_b , but using the values calculated when creating the handle. Further, our optimization looks like this: fhnd_GetJ4=GetJ4(a,b,x); optimal_x=fminbnd(fhnd_GetJ4,0,1,opt); And this optimization is performed in 0.8 ms.
Result
We obtained the same speed as with the explicit transfer of calculations in the example with
GetJ2 , but preserved the integrity of the function and the convenience of its use.In the future, if you intend to use the function both for optimization and just for computing, then you can add one optional parameter flag to it. If it is not specified, the function returns a value. If set, the handle to the nested function is returned.
Source: https://habr.com/ru/post/199300/
All Articles