Squeak: Simulation of Queuing Systems

On Habré there is very little information about such a programming language as Squeak . I will try to talk about it in the context of simulation of queuing systems . I will show you how to write a simple class, tell you its structure and use it in a program that will serve applications through several channels.

A few words about Squeak

Squeak is an open, cross-platform implementation of the Smalltalk-80 programming language with dynamic typing and garbage collection. The interface is quite specific, but quite convenient for debugging and analysis. Squeak fully complies with the concept of OOP. Everything consists of objects, even if-then-else, for, while constructs are implemented with their help. The entire syntax is reduced to sending the message object in the form:

<object> <message>

Any method always returns an object and you can send a new message to it.
Squeak is often used to model processes, but it can also be used as a tool for creating multimedia applications and a variety of educational platforms.

Queuing systems

Queuing systems (QS) contain one or several channels that process applications coming from several sources. The service time for each application can be fixed or arbitrary, as well as the intervals between their receipt. This could be a telephone exchange, laundry, cashiers in the store, a typewriting bureau, etc. It looks like this:


The QS includes several sources that enter the common queue and are sent for servicing as the processing channels become free. Depending on the specific features of real systems, the model may contain a different number of sources of requests and service channels and have different limits on the queue length and the associated possibility of losing requests (refusals).
')
In the simulation of QS, problems of estimating the average and maximum queue lengths, the frequency of service failures, the average load on channels, and the determination of their number are usually solved. Depending on the task, the model includes program blocks for collecting, accumulating and processing the necessary statistical data on the process behavior. The most frequently used models of event flows in the analysis of QS are regular and Poisson. Regular ones are characterized by the same time between occurrences of events, and Poisson ones are random.

A bit of math

For a Poisson flow, the number of events X falling in the interval of length τ (tau) adjacent to the point t is distributed according to the Poisson law:


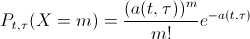
where a _{(t, τ)} is the average number of events occurring on the time interval τ .
The average number of events occurring per unit time is equal to λ (t) . Consequently, the average number of events in the time interval τ adjacent to the time t , will be equal to:


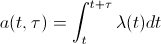
The time T between two events at λ (t) = const = λ is distributed according to the law:


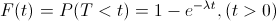
The distribution density of a random variable T has the form:


To obtain pseudo-random Poisson sequences of time intervals t _i solve the equation:


where r _i is a random number uniformly distributed on the interval [0, 1].
In our case, this gives the expression:


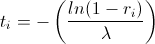
By generating random numbers, you can write whole volumes. Here, to generate integers uniformly distributed on the interval [0, 1], we use the following algorithm:


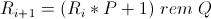
where R _i is another random integer;
P - some large prime number (for example 2311);
Q - integer - the upper limit of the interval, for example, 2 ²¹ = 2097152;
rem is the operation to get the remainder from dividing integers.

The initial value of R _{0 is} usually set arbitrarily, for example, using the timer readings:

Time totalSeconds 

To obtain numbers evenly distributed on the interval [0, 1], we use the language operator:

r: = (r / q) asFloat

Rand class

To obtain random numbers uniformly distributed on the interval [0, 1], create a class - the generator of real numbers:

 Float variableWordSubclass: #Rand " " instanceVariableNames: '' " " classVariableNames: 'R' " " poolDictionaries: '' " " category: 'Sample' " " 

Methods:

 "" init R := Time totalSeconds.next "  " next R := (R * 2311 + 1) rem: 2097152. ^(R/2097152) asFloat 

To set the initial state of the sensor, send a Rand init message.
For receiving the next random number we send Rand next .

Application Processing Program

So, as a simple example, we will do the following. Suppose we need to simulate the maintenance of a regular flow of requests from one source with a random time interval between requests. There are two channels of different performance, allowing to serve applications for 2 and 7 time units, respectively. It is necessary to register the number of applications served by each channel in the interval of 100 time units.


At startup, we see that process 1 managed to process 31 applications, and process 2 only 11: