DGFS - do-it-yourself fast file system
Sometimes file system tools have to store a lot of information, most of which are static. When there are few files and they are large, it is tolerable. But if the data is in a huge number of small files, access to which is pseudo-random, the situation is approaching a catastrophe.

I believe that a specialized read-only file system, other things being equal, has advantages over this general purpose, because:
')
In this article, we will understand how to organize a file system, with the objective function of maximum performance at minimum cost.
First of all, the drive: all experiments are performed on a dedicated Seagate Barracuda ST31000340NS with a capacity of 1 Tb.
The operating system is Windows XP.
Processor: AMD Athlon II X3 445 3 GHz.
Memory: 4 GB.
Before starting a meaningful job, I want to understand what to expect from the disk. Therefore, a series of measurements of random positioning and disk readings were made.
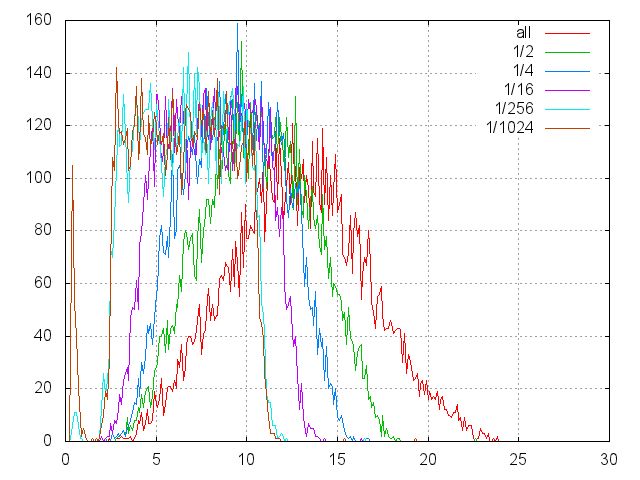
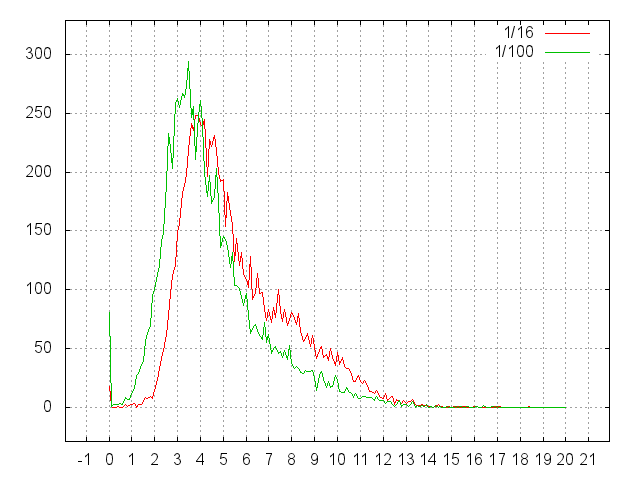
The presented graph shows histograms of reading times from the disk in arbitrary positions. The abscissa axis shows the duration of positioning and reading. The ordinate is the number of hits in a basket 0.1 msec wide.
Appeals to the disk were made in a regular manner:
Several series of measurements were made, 10,000 in each series. Each series is marked by its color:
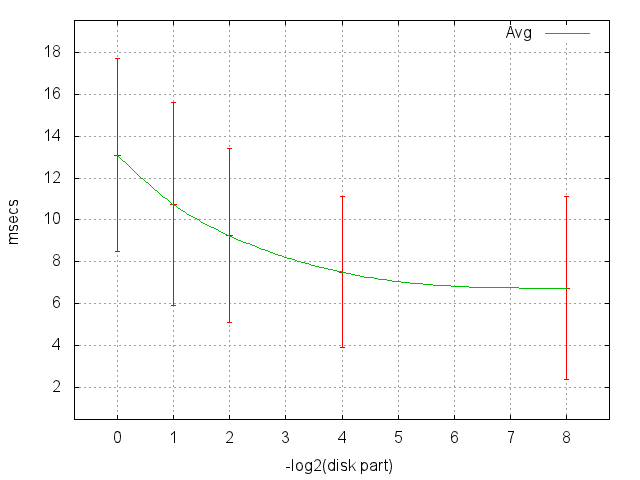
And here are the mat. expectations and errors from the previous graph, the x-axis on a logarithmic scale, for example, 1/16 corresponds to 4 (1/2 ** 4).
What conclusions can be made?
Let's try to create a file the size of a disk and get the temporary characteristics of working with it. To do this, create a file commensurate with the size of the file system and read it in random places with regular _fseeki64 / fread .
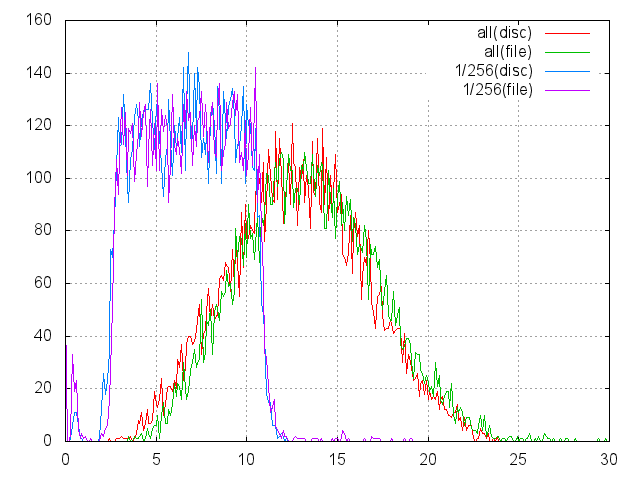
The graph similar to the previously presented histograms. And two of them, marked as (disc), are taken from the previous chart. Paired histograms, labeled as (file), are derived from measurements of file readings. What can be noted:
That is, it is necessary to spend an extra byte for every kilobyte of data, a gigabyte goes to a terabyte, and it's not so easy to cache a gigabyte. However, ext4 seems to have no such problem, or it is masked with extents.
Let us recall about our test problem and try to solve it in the forehead with the help of the file system. It immediately turns out that:
First, consider the histogram in milliseconds:
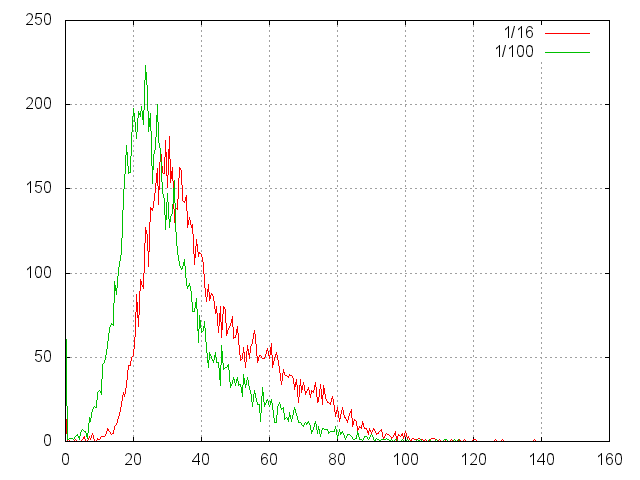
So, here is a histogram of read times of random files.
And now take a look at the same in terms of conditional seek'ov:
Let's build a prototype of our read-only filesystem:
The following are histograms of times obtained from these data:
Here is the time to ask - well, we have made out a very special case of a regularly arranged file system (three levels with fixed names). And what about the usual data, with the usual paths and names?
The answer is that nothing will change in principle. There will still be one main index. But it will be arranged a little differently.
The above file ID (index key) was the encoded path to it. So it will be, the key is the string full path to the file. Everything else in meaning - size, position, owner, group, rights ...
It is possible that there will be not so many combinations (owner, group, rights) and it will be advantageous to store them with Huffman codes indicating the global table of combinations. But these are details. In principle, the situation is no different from the one we have already tried.
To find a file, you need to specify its full path. To view the contents of a directory, you need to specify the path of the directory and select everything that matches the prefix. To move up the hierarchy, bite off a piece of the path and again look for the prefix.
But do file paths take up a lot of space? Yes, but files in one directory have a common prefix that can be stored only once. The common suffix is also common. To understand the amount of data that needs to be stored, a series of experiments with file system paths were performed, which showed that they were compressed by an average of 10 times using bzip2 (BWT + suffix sort + huffman). Thus, it remains 5-6 bytes per file.
In total, you can count on 10-16 bytes per file, or ~ 2 bytes per kilobyte of data (if the average file is 8K). To a terabyte file, you need a 2 gigabyte index, a regular 64 gigabyte SSD disk, therefore, it can serve 32 terabytes of data.
Full counterparts and difficult to produce.
For example, SquashFS , with zero compression can be used in a similar way. But this system repeats the traditional structure, it simply compresses files, inodes and directories. Therefore, all those bottlenecks that we diligently tried to avoid were inherent.
An exemplary analogue is the use of a DBMS for data storage. In fact: we store the contents of files as blobs, and metadata as attributes of a table. Simple and elegant. The DBMS itself takes care of how to efficiently place files in the available disk space. Itself creates and maintains all the necessary indices. Plus a nice bonus - we can change our data without restrictions.
But:
Obviously, the disposable file system is not needed by anyone. Time to fill a file system of several terabytes may take tens of hours. During this time, new changes may accumulate, therefore, there must be a method for changing data that is different from a full update. In this case, it is desirable not to stop work. Well, this topic is worthy of a separate story, and over time we are going to talk about it.
So, a prototype of the read-only file system is presented that is simple, flexible, solves a test problem, and at the same time:

I believe that a specialized read-only file system, other things being equal, has advantages over this general purpose, because:
')
- not necessary to manage free space;
- no need to spend money on journaling;
- you can not worry about fragmentation and store files continuously;
- it is possible to collect all the meta-information in one place and effectively cache it;
- sin not to compress the meta-information, since it was in one heap.
In this article, we will understand how to organize a file system, with the objective function of maximum performance at minimum cost.
Task
- 100 million small files (~ 8K each).
- Three-level hierarchy - 100 top-level directories, each of which has 100 directories of the middle level, each of which has 100 directories of the lower level, each of which has 100 files.
- We optimize the build time and the average time to read a random file.
Iron
First of all, the drive: all experiments are performed on a dedicated Seagate Barracuda ST31000340NS with a capacity of 1 Tb.
The operating system is Windows XP.
Processor: AMD Athlon II X3 445 3 GHz.
Memory: 4 GB.
Disk characteristics
Before starting a meaningful job, I want to understand what to expect from the disk. Therefore, a series of measurements of random positioning and disk readings were made.

The presented graph shows histograms of reading times from the disk in arbitrary positions. The abscissa axis shows the duration of positioning and reading. The ordinate is the number of hits in a basket 0.1 msec wide.
Appeals to the disk were made in a regular manner:
- opening via CreateFile ("\\\\. \\ PhysicalDrive1" ...);
- positioning via SetFilePointer;
- and reading through ReadFile.
Several series of measurements were made, 10,000 in each series. Each series is marked by its color:
- all - positioning goes around the disk;
- ½ - only in its younger half, etc.

And here are the mat. expectations and errors from the previous graph, the x-axis on a logarithmic scale, for example, 1/16 corresponds to 4 (1/2 ** 4).
What conclusions can be made?
- In the worst case (random search), the expectation of a single reading is 13 msec. That is, more than 80 random reads per second from this disk can not be done.
- At 1/256 we see the cache hit for the first time.
- At 1/1024, a noticeable number of readings of ~ 1% begins to fall into the cache.
- 1/256 doesn’t differ from 1/1024 anymore, the run-through of the heads is already too small, we see only their overclocking and (mostly) calm.
- We have the ability to scale, that is, it is permissible to carry out experiments on a partially filled disk and quite confidently extrapolate the results.
NTFS
Let's try to create a file the size of a disk and get the temporary characteristics of working with it. To do this, create a file commensurate with the size of the file system and read it in random places with regular _fseeki64 / fread .

The graph similar to the previously presented histograms. And two of them, marked as (disc), are taken from the previous chart. Paired histograms, labeled as (file), are derived from measurements of file readings. What can be noted:
- Times are close.
- Although the file is 90% of the file system (9xE11 bytes), reading from it at full size is, on average, almost a millisecond slower.
- Disk cache for a file works better than for a disk.
- Tails appeared at ~ 6 msec, if the worst time for full reading was about 24 msec, now it stretches to almost 30. Similarly, for 1/256. Apparently, the metadata fell out of the cache and they have to additionally read.
- But in general, reading from a large file works very much like working with a bare disk, and in some cases can replace or emulate it. This makes NTFS honored, because for example, the ext2 / ext3 structure requires a minimum of 4-byte number for every 4-Kb data block:
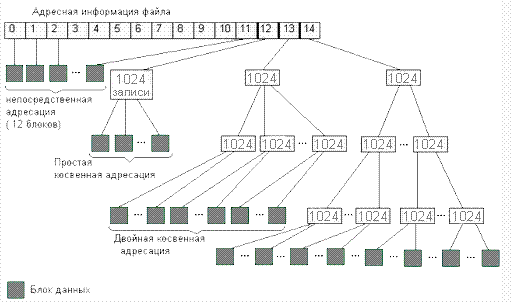
That is, it is necessary to spend an extra byte for every kilobyte of data, a gigabyte goes to a terabyte, and it's not so easy to cache a gigabyte. However, ext4 seems to have no such problem, or it is masked with extents.
NTFS with hierarchy
Let us recall about our test problem and try to solve it in the forehead with the help of the file system. It immediately turns out that:
- It takes a lot of time, it takes about half an hour to create one branch out of a million files, with a tendency to gradually slow down as the disk is filled in accordance with our first schedule.
- Creating all 100 million files would therefore take 50+ hours.
- Therefore, we will take measurements on 7 million files (~ 1/16) and scale to the complete task.
- Attempting to make measurements in more close to combat conditions led to the fact that NTFS collapsed on the 12th million files with approximately the same diagnostics that the main character received in the film “Death to her face”: - “Actually, fragmented cervical vertebra, this is a very, VERY bad sign! ”
First, consider the histogram in milliseconds:

So, here is a histogram of read times of random files.
- Two series — 7 million as 1/16 tasks and 1 million for calibration.
- In a series of 10,000 measurements, in a basket 0.5 msec.
- The total time of 1/16 of the test is 7'13 ", that is, the expectation is 43 msec.
- The total time of 1/100 test is 5'20 '', that is, the expectation is 32 msec.
And now take a look at the same in terms of conditional seek'ov:

- That 1/16, that 1/100, is too large to be effectively cached. And our files are too small for fragmentation.
- Therefore, we need to pay 1 for reading the actual data. Everything else - the internal affairs of the file system.
- The maxima are at 3.5 (for 1/100) and 4 (for 1/16) seek.
- And the expectation is generally 4 ... 5.
- That is, to get to the information about where the file is stored, the file system (NTFS) has to do 3-4 readings. And sometimes more than 10.
- In the case of a complete task, one must assume that the situation will not improve.
Prototype
Let's build a prototype of our read-only filesystem:
- It consists of two files - data and metadata.
- The data file is simply all the files recorded in a row.
- Metadata file - In-tree with key - file identifier. The value is the address in the data file and its size.
- The file identifier is the coded path to it. Recall that our data is located in a three-level directory system, where each level is encoded by a number from 0 to 100, and the file itself is similar. This whole structure is packaged as an integer.
- The tree is written in the form of 4K pages, primitive compression is applied.
- In order to avoid fragmentation, these files have to be created in different file systems.
- Simply appending data to the end of the file (data) is ineffective. The larger the file, the more it costs the file system (NTFS, WinXP) its extension. To avoid this non-linearity, you have to pre-create the file of the desired size (900 GB).
- It takes this preliminary creation of more than 2 hours, all this time it takes to fill this file with zeros, apparently for security reasons.
- The same time it takes to fill this file with data.
- Building an index takes about 2 minutes.
- Recall only 100 million files, each about 8K in size.
- Index file is 521 MB. Or ~ 5 bytes per file. Or ~ 5 bits per kilobyte of data.
- A variant of the index with more complex compression (Huffman codes) was also tested. This index occupies 325 MB. Or 3 bits per kilobyte of data.
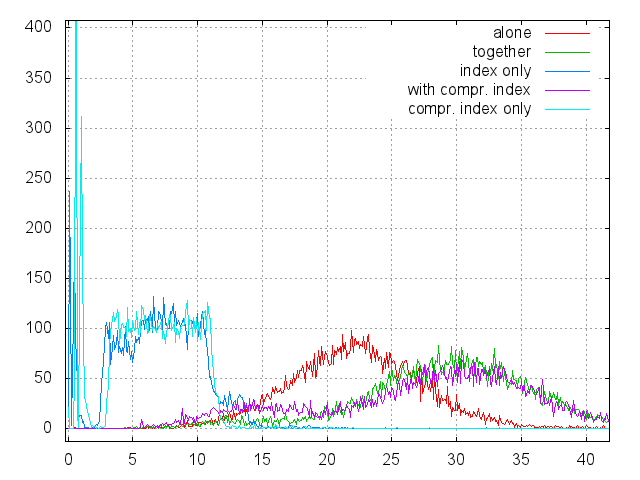
The following are histograms of times obtained from these data:

- “Alone” - under this label is the data file, located separately from the index file, on another physical disk;
- "Ogether" - both the data file and the index are located within the same file system on the same physical disk;
- “Index only” - only search for information about the file in the index is performed without reading the actual data;
- “With compr. index "- the same as" together ", but with a compressed index;
- “Compr. index only - the same as “index only”, but with a compressed index;
- only 10,000 readings, histogram step 0.1 msec.
Findings:
- The quality of index compression almost does not affect the speed of work. CPU time is wasted on the release of pages, but the page cache works better.
- Reading the index looks like one reading from a file of the appropriate size (see the first chart). Since 512 MB is a 1/2000 disk, the average seek time should be about 6.5 msec, plus the surcharge for what we read from the file, and not directly from the disk. Apparently, this is it. The index tree is three-level, the top two levels are very fast in the cache, and the bottom level of pages is pointless to cache. As a result, any search in the tree degenerates into a single leaf page reading.
- If the data file and the index file are located on the same physical disk, the total search time is two random seek for the full distance. One to read the data and one to go to the index file, which is located either at the very beginning or at the very end of the disk.
- If the files are separated by different devices, we have one full seek to read the data and one short look in the index. Given that the index file is relatively small, a natural solution suggests itself - if we need a storage of several (tens) terabytes, we need to prepare a dedicated disk for the index (SSD) and several disks for the data. It can be designed as a JBOD and looks like a regular file system.
- This scheme has an important feature - guaranteed response time, which is difficult to achieve in conventional file systems, for example, for use in real-time systems.
Here is the time to ask - well, we have made out a very special case of a regularly arranged file system (three levels with fixed names). And what about the usual data, with the usual paths and names?
The answer is that nothing will change in principle. There will still be one main index. But it will be arranged a little differently.
The above file ID (index key) was the encoded path to it. So it will be, the key is the string full path to the file. Everything else in meaning - size, position, owner, group, rights ...
It is possible that there will be not so many combinations (owner, group, rights) and it will be advantageous to store them with Huffman codes indicating the global table of combinations. But these are details. In principle, the situation is no different from the one we have already tried.
To find a file, you need to specify its full path. To view the contents of a directory, you need to specify the path of the directory and select everything that matches the prefix. To move up the hierarchy, bite off a piece of the path and again look for the prefix.
But do file paths take up a lot of space? Yes, but files in one directory have a common prefix that can be stored only once. The common suffix is also common. To understand the amount of data that needs to be stored, a series of experiments with file system paths were performed, which showed that they were compressed by an average of 10 times using bzip2 (BWT + suffix sort + huffman). Thus, it remains 5-6 bytes per file.
In total, you can count on 10-16 bytes per file, or ~ 2 bytes per kilobyte of data (if the average file is 8K). To a terabyte file, you need a 2 gigabyte index, a regular 64 gigabyte SSD disk, therefore, it can serve 32 terabytes of data.
Analogs
Full counterparts and difficult to produce.
For example, SquashFS , with zero compression can be used in a similar way. But this system repeats the traditional structure, it simply compresses files, inodes and directories. Therefore, all those bottlenecks that we diligently tried to avoid were inherent.
An exemplary analogue is the use of a DBMS for data storage. In fact: we store the contents of files as blobs, and metadata as attributes of a table. Simple and elegant. The DBMS itself takes care of how to efficiently place files in the available disk space. Itself creates and maintains all the necessary indices. Plus a nice bonus - we can change our data without restrictions.
But:
- Ultimately, the DBMS still accesses the disk, directly or through the file system. And it is fraught with danger, it is worth overlooking and - bang! work time has slowed down at times. But, let's say, we have an ideal DBMS, with which this will not happen.
- A DBMS cannot compress prefixes just as efficiently simply because it is not designed for a read-only mode.
- The same can be said about the metadata - in the database they will take up much more space.
- More space — more disk readings — slower work.
- Using hash codes from the file path does not solve the problem. the path matching the hash code still needs to be stored somewhere just to ensure that the contents of the directory can be viewed. Everything will result in the fact that it is necessary to reproduce the structure of the file system by means of the DBMS.
- Files larger than a page will be forced to split the DBMS into parts, and random access to them will be carried out at best for a logarithmic time of file size.
- If we can simply place all the metadata on a dedicated SSD disk, in the case of a DBMS, this will be much more difficult.
- You can forget about the guaranteed response time.
Transactional
Obviously, the disposable file system is not needed by anyone. Time to fill a file system of several terabytes may take tens of hours. During this time, new changes may accumulate, therefore, there must be a method for changing data that is different from a full update. In this case, it is desirable not to stop work. Well, this topic is worthy of a separate story, and over time we are going to talk about it.
Total
So, a prototype of the read-only file system is presented that is simple, flexible, solves a test problem, and at the same time:
- demonstrates the maximum possible performance on the gland allocated for it;
- its architecture does not impose objective restrictions on the amount of data;
- lets you know what you should do to get a general-purpose file system, rather than an odd job
- makes it clear which way to go in order to make our file system incrementally changeable.
Source: https://habr.com/ru/post/198564/
All Articles