Using the Haar cascade to compare images

The signs of Haar, about which I will tell, are known to most people who are somehow connected with the recognition and machine learning systems, but, apparently, few people use them to solve problems outside the standard field of application. The article is devoted to the use of the Haar cascades for comparing close images, in object tracking tasks between adjacent video frames, matching search on several photos, image search on the image and other similar tasks.


In most cases, when a simple comparison of two rather similar fragments of an image is needed, it is realized through their covariance (or something similar). A sample is taken (in the photo is a flower) and moves along the image along X and Y in search of a point where the difference between the sample ( J ) and the image ( I ):

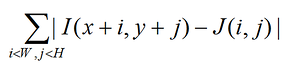
reaches its minimum.

This method is very fast to implement, intuitive and well known. Perhaps I have not met a single group of developers, wherever it was used. Of course, everyone perfectly knows his flaws:

• Instability when changing lighting
• Instability when zooming or rotating an image
• Instability if part of the image is a changing background
• Low speed - if you need to find the region n * n in the image m * m, then the number of operations will be proportional to n2 (mn) 2.

How to deal with these shortcomings, everyone also knows.

• Illumination is neutralized by normalization or transition to binarization of the region .
• Changes in scale and small turns are neutralized by changing the resolution during correlation.
• With this approach, no one fights.
• The speed is optimized by searching with a big step or with a small resolution.

In situations where the results of the correlation are not enough - go to more complex methods, such as comparing point of interest ( SURF ) maps, boundaries, or directly selecting objects. But these algorithms are completely different: in most cases they are quite slow, they are difficult to write from scratch (especially on some DSP processor), there are restrictions on the image structure.

At some point, while thinking about another project, I rested on a task where it was necessary to compare several changeable areas in the image. And I thought until I remembered the Predator algorithm once mentioned on Habré, where fast and stable object tracking was shown in the video. After a little reflection, I realized that this whole approach, which allowed solving a large class of problems, passed by me.
Let me remind you that such signs of Haar. Cascades of features are commonly referred to as a base for building systems for the extraction of complex objects, such as faces , hands, or other objects . In most articles, this approach is inextricably linked with the AdaBoosta learning algorithm . By itself, the Haar cascade is a set of primitives for which their convolution with an image is considered. The simplest primitives are used, consisting of rectangles and having only two levels, +1 and -1. In addition, each rectangle is used several times of different sizes. Convolution here means s = XY , where Y is the sum of the image elements in the dark area, and X is the sum of the image elements in the light area (you can also take X / Y , then there will be stability when changing the scale).

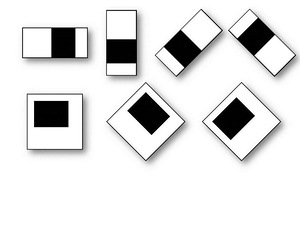
Such convolutions emphasize the structural information of an object: for example, the following convolution will always be negative for the center of a person’s face:

The eyes will be darker than the area between them, just as the area of ​​the mouth will be darker than the forehead. The more various primitives are used, the more accurately the object can be classified. Moreover, if the exact classification is not needed - you can use a smaller number of primitives.
Here we can mention that in the object recognition problem, after the feature sets have been constructed from the test sample, the learning algorithms ( AdaBoost , SVM ) determine the sequence (cascade) of the bundles corresponding to the object. When an object is recognized on an image, it is compared with a test image.
What is the plus of Haar and why it is impossible to use such remarkable and physical curves as, for example, sinusoids and Gaussians instead of these ugly rectangles?
Plus the fact that the Haar cascades are very quickly calculated through the integral representation of the images . This is described in more detail by reference, and here I will only briefly say that the integral image is represented as:

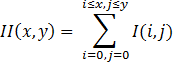
The value at point X, Y of the matrix ( II ) obtained from the original image ( I ) is the sum of all points in the rectangle (0.0, X, Y). Then the integral over any rectangle (ABCD) in the image is represented as:
SumOfRect (ABCD) = II (A) + II (C) - II (B) - II (D)
This gives only 4 memory accesses and 3 mathematical operations for calculating the sum of all elements of a rectangle, regardless of its size. When calculating other convolutions other than Haar primitive convolutions, the number of actions required is proportional to the square of the primitive size (if you do not count through the FFT, which is not possible for any patterns).
Let's return to our task. Suppose we want to find a small fragment ( J ) in a large image ( I ). No training is required to do this. One fragment is still impossible to produce. The primitives of Haar will help to get an image of J and look for it on I. It is enough to obtain convolutions of J with a set of Haar-signs and compare them with the set of convolutions of the same primitives calculated for I in windows proportional to a small fragment.
Pros:

• Resistance to changing lighting, even if it is a local change of lighting, resistance to noise (primitives are the simplest band-pass filter ).
• If the primitives were not very small, then the correlations are much more stable with the change of scale (the size of the primitives will not affect the accuracy if the walk is a short step).
• If the signs on a large image are calculated in advance and when you shift the search window, you take the already calculated and relevant for him - the search will be much faster than the correlation (you need to compare fewer elements).

At the same time, it can be seen that a number of fairly simple optimizations can be made that will speed up and refine this approach.
If someone wanted to play, I wrote a small program that implements the simplest version of this algorithm. The program maintains the selected fragment in the video stream. EmguCV for hooking up the camera and simple image transformations (Haar is done manually).