About stars
Sometimes I get tasks that have no obvious practical value, but, nevertheless, they capture my imagination one way or another, at least until I decide. The practical value of the task, as a rule, is zero, but in the process others are solved that may be of greater value than the solved one.
It all started with a desire to study the properties of regular octagons and octagrams, but the results turned out to be applicable to all convex polygons (polygons) and stars built in them (by analogy, I will call them polygrams - pentagram, hexagram, setagram, octagram, etc. - although the term has other meanings).
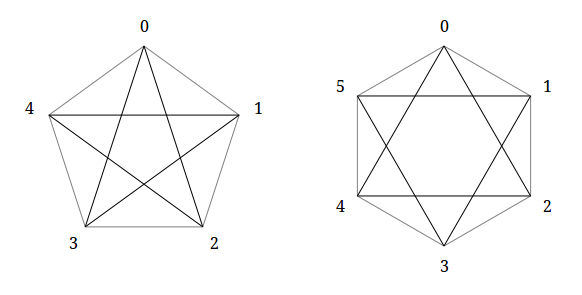
To begin with the terminology. A pentagram is a collection of all the diagonals of a pentagon; in the case of a hexagram, these are not all diagonals, but only those that connect non-opposite vertices of a hexagon. In both cases, these vertices go through one from each other. For example, if the vertices of the pentagon are renumbered(0, 1, 2, 3, 4) , then the pentagram is a collection of lines (0, 2) , (1, 3) , (2, 4) , (3, 0) , (4, 1) . Hexagram (0, 1, 2, 3, 4, 5) , respectively, is a collection of lines (0, 2) , (1, 3) , (2, 4) , (3, 5) , (4, 0) , (5, 1) . As a starting point, the zeros are not taken by chance or as a tribute to programmatic thinking; I will describe the convenience of this designation below. The lines that make up the polygram will be called the edges. I will call the vertices of a polygram vertices of the original polygon, and not all the intersection points of the edges.
')
The definition can be generalized by introducing the concept “order of a polygram” as some integer k, having a range of values between 1 and n / 2, where n is the number of corners of the original polygon. The upper bound of k (equal to the integer part ofn / 2 ) will determine the number of different generalized polygrams. The order itself denotes which vertex from the original should be connected by a diagonal entering the polygram. What does it mean? If we consider the numbers of the vertices of the polygram, starting from zero, then they form an additive residue group modulo n. Let m be the vertex number of the polygram. Then the segment connecting the vertex m and m + k (where k is the order of the polygram) in this group will be part of the polygram of order k. In this generalization, a polygram of order 1 coincides with the original polygon.
In the case of the pentagon according to the formula, there are two generalized pentagrams - the pentagon itself and the pentagram in the classical sense.

In the case of a hex, there are three generalized hexagrams: the hexagon itself, the classical hexagram, and the diagonals connecting the opposite vertices (a degenerate case).

For a better illustration I will analyze the polygrams for the septagon and the octagon. According to the formula, the number of septagrams will be three, the number of octagrams is four.

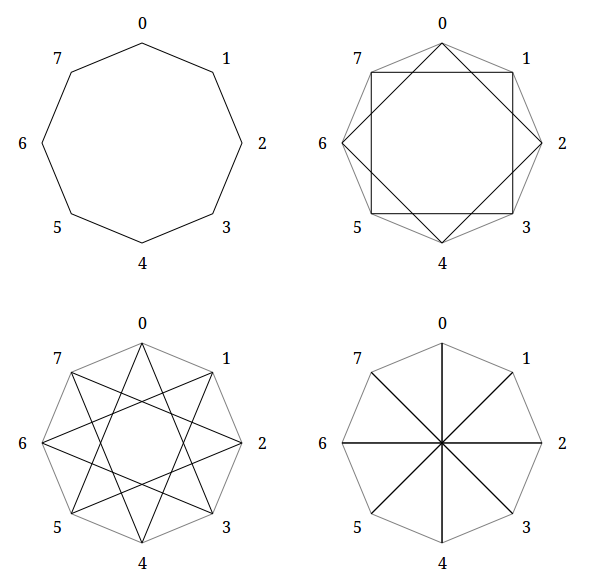
As a side effect, you can see that polygrams are naturally divided into connected and incoherent. Connected polygrams are polygrams, between any pair of vertices of which there is a path along the edges (jump from edge to edge is possible only at the vertices of the polygon). Using the theory of numbers, you can see that polygrams are connected if and only if the number of corners of the original polygon and the order of the polygram are coprime numbers.
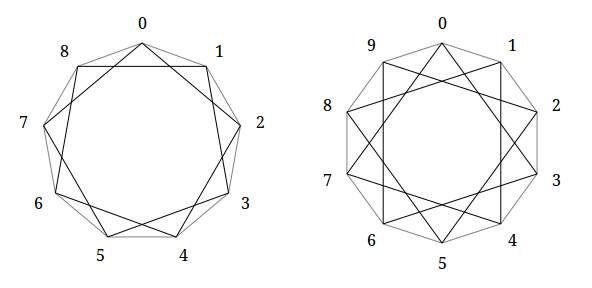
The picture below shows examples of disconnected polygrams, their individual parts are highlighted in different colors. The non-gram(n = 9, k = 3) is divided into three triangles, the decagram (n = 10, k = 4) - into two pentagrams:

Now polygrams with the same number of angles (n = 9, k = 2 and n = 10, k = 3 ), but already connected:
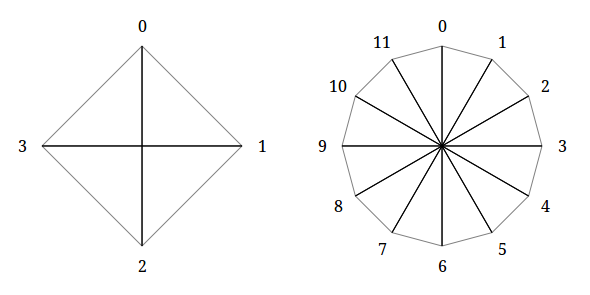
In addition, in the case of even n and maximum for such a case k (k = n / 2), the polygrams degenerate into a set of diagonals connecting opposite vertices.
A rather unexpected result for me was that the sum of the angles at the vertices of the polygrams (in the case of convex polygons) is a fairly simple computable value:π (n - 2k) . In the case of first-order polygrams (which coincide with the original polygon), the formula reduces to the well-known formula for calculating the angles of a polygon, but in the case of a degenerate polygram, the sum of the angles turns out to be zero (which is natural). The proof of this fact is as follows: each edge of the polygram (for 1 <k <n / 2 - the case of a degenerate polygram is dropped and coincides with the original polygon) divides the polygon into two: one with k + 1 angle, the other with n - k + 1 . Summing the sum of the angles of all the smaller angles of the parts (which are with k + 1 angle), we get the result π (k - 1) n (for each vertex of the polygon there is one (k + 1) -gon ). Every whole corner of the original polygon is present k - 1 times . Plus, angles that are adjacent to the angles of the polygrams are present once, If we subtract the sum of the whole angles of the polygrams (which is π (n - 2) (k - 1)) from the first sum, since each integer angle occurs k - 1 times ), we get the sum of the angles π (k - 1) n - π (n - 2) (k - 1) adjacent to the angles of the polygram. If we now subtract this sum of angles from the sum of the angles of the original polygon, we get the sum of the angles of the polygram:
π (n - 2) - (π (k - 1) n - π (n - 2) (k - 1)) = π (n - 2) - π (k - 1) n + π (n - 2) (k - 1) = π (n - 2) k - π (k - 1) n = π (n - 2k)
All the illustrations and reasoning above applied to any polygrams constructed on convex polygons. In the pictures I depicted cases of regular polygrams solely from my own laziness - it was easier to write a drawing program. The following discussion focuses only on the correct polygrams.
Based on the formula above, the angle at the vertex of a regular polygram isπ - 2πk / n .
If we take the horizon (the set of external points) of a regular polygram, then this figure will be a nonconvex 2n-gon (n is the number of vertices of the polygram. The borders of the figures on the right illustrate this:

Thus, another n “extra” angles appear, which I will call the inner corners of the polygram. These angles are not convex, from the formula for the sum of the angles of a polygon for a regular polygram, they are(π (2n - 2) - π (n - 2k)) / n = π (n + 2k - 2) / n = π + 2π (k - 1 ) / n . The angles opposite to them are equal, respectively, π - 2π (k - 1) / n . This angle I will call the angle between the rays.
These calculations can be useful for constructing patterns and amusing ornaments, which will be illustrated below for patient readers.
Next comes a rather useless part, which gave me aesthetic pleasure at one time, but the result of which can only be a reader’s wasted time, which was the reason for adding “Funny Tasks” to the habr.
It all started with a desire to study the properties of regular octagons and octagrams, but the results turned out to be applicable to all convex polygons (polygons) and stars built in them (by analogy, I will call them polygrams - pentagram, hexagram, setagram, octagram, etc. - although the term has other meanings).
To begin with the terminology. A pentagram is a collection of all the diagonals of a pentagon; in the case of a hexagram, these are not all diagonals, but only those that connect non-opposite vertices of a hexagon. In both cases, these vertices go through one from each other. For example, if the vertices of the pentagon are renumbered
')

The definition can be generalized by introducing the concept “order of a polygram” as some integer k, having a range of values between 1 and n / 2, where n is the number of corners of the original polygon. The upper bound of k (equal to the integer part of
In the case of the pentagon according to the formula, there are two generalized pentagrams - the pentagon itself and the pentagram in the classical sense.

In the case of a hex, there are three generalized hexagrams: the hexagon itself, the classical hexagram, and the diagonals connecting the opposite vertices (a degenerate case).

For a better illustration I will analyze the polygrams for the septagon and the octagon. According to the formula, the number of septagrams will be three, the number of octagrams is four.


As a side effect, you can see that polygrams are naturally divided into connected and incoherent. Connected polygrams are polygrams, between any pair of vertices of which there is a path along the edges (jump from edge to edge is possible only at the vertices of the polygon). Using the theory of numbers, you can see that polygrams are connected if and only if the number of corners of the original polygon and the order of the polygram are coprime numbers.
The picture below shows examples of disconnected polygrams, their individual parts are highlighted in different colors. The non-gram

Now polygrams with the same number of angles (

In addition, in the case of even n and maximum for such a case k (k = n / 2), the polygrams degenerate into a set of diagonals connecting opposite vertices.

A rather unexpected result for me was that the sum of the angles at the vertices of the polygrams (in the case of convex polygons) is a fairly simple computable value:
All the illustrations and reasoning above applied to any polygrams constructed on convex polygons. In the pictures I depicted cases of regular polygrams solely from my own laziness - it was easier to write a drawing program. The following discussion focuses only on the correct polygrams.
Based on the formula above, the angle at the vertex of a regular polygram is
If we take the horizon (the set of external points) of a regular polygram, then this figure will be a nonconvex 2n-gon (n is the number of vertices of the polygram. The borders of the figures on the right illustrate this:

Thus, another n “extra” angles appear, which I will call the inner corners of the polygram. These angles are not convex, from the formula for the sum of the angles of a polygon for a regular polygram, they are
These calculations can be useful for constructing patterns and amusing ornaments, which will be illustrated below for patient readers.
Next comes a rather useless part, which gave me aesthetic pleasure at one time, but the result of which can only be a reader’s wasted time, which was the reason for adding “Funny Tasks” to the habr.
Octagram Pattern
When k = 2, the angle between the rays will be equal to π - 2π / n , which is exactly equal to the angle of the original polygon in which the polygram is constructed. In what cases such polygons will closely adjoin each other, forming a semblance of a mosaic? In other words, the sum of the angle at the vertex of the polygram plus the double angle at the vertex of the polygon should be 2π. The angle at the vertex of the regular polygram in this case is π - 4π / n . Thus, we get the equation:
π - 4π / n + 2 (π - 2π / n) = 2π
3π - 8π / n = 2π
8π / n = pi;
n = 8
Thus, the octagram with k = 2 can be obtained by drawing 8 octagons, the neighboring of which have a common side - the inner sides of such polygons form the horizon of such an octogram.

The octogram(n = 8, k = 2) is disconnected and consists of two squares (the angles are straight at all vertices: π - 4 π / 8 = π / 2 ). On the rays of such an octagram, one can construct squares with a side equal to the side of the ray.
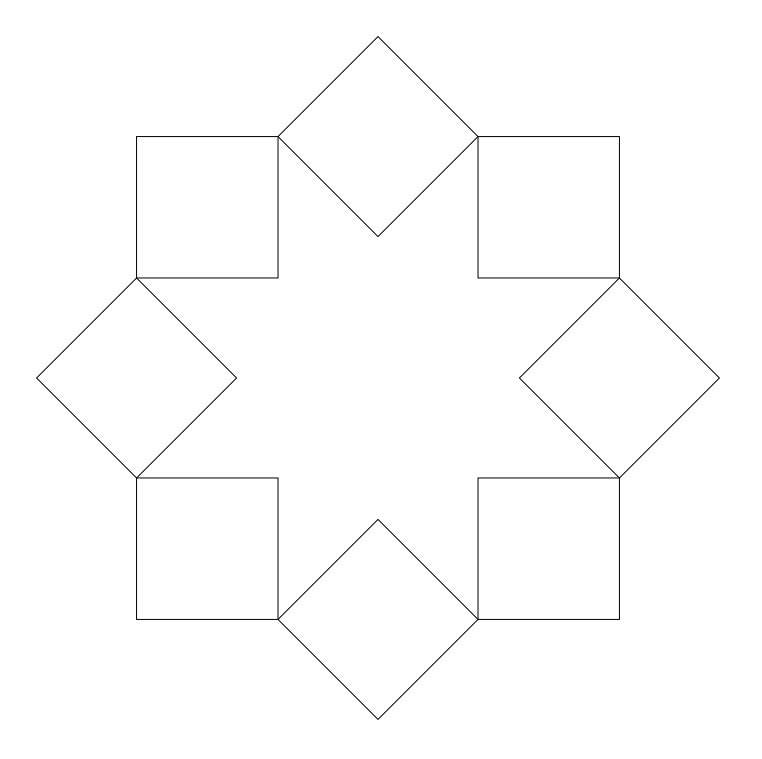
The internal angle of this octagram is5π / 4 . Subtracting from the internal angle the sum of the angles of the squares built on the beams, we get the angle between the sides of the adjacent squares inside the octogram. This angle is π / 4 . Thus, the inner sides of the squares form a star-shaped figure with angles at eight vertices π / 4 and angles between the rays π / 2 (the angle at the vertex of the square). Thus, the internal angles of this figure will be equal to 3π / 2 .
If we now consider the angles of the octagram(n = 8, k = 3) , we find that the vertex angle is π - 2πk / n = π / 4 , and the internal angles π + 2π (k - 1) / n = 3π / 2 , that exactly corresponds to the figure bounded by the squares described above.
An illustration of these calculations can be a pretty picture:
Thus, the octagram with k = 2 can be obtained by drawing 8 octagons, the neighboring of which have a common side - the inner sides of such polygons form the horizon of such an octogram.

The octogram

The internal angle of this octagram is
If we now consider the angles of the octagram
An illustration of these calculations can be a pretty picture:

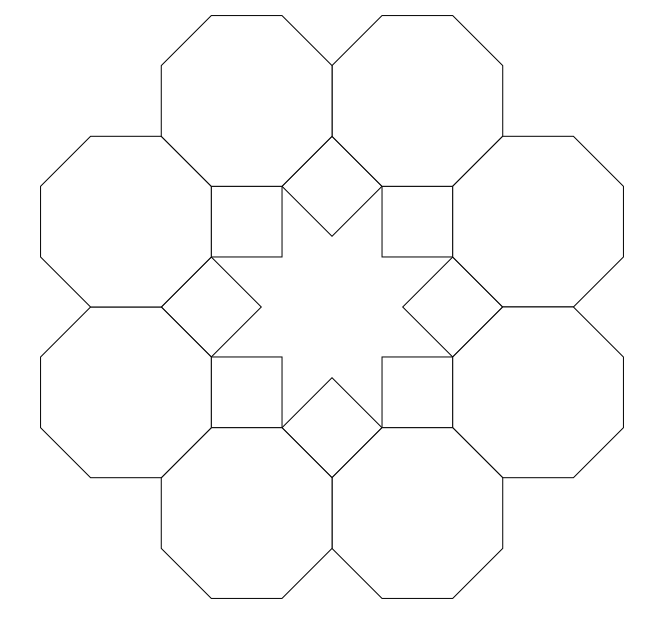
Hexagon hexagram mosaic
Consider again the case of k = 2 . As was described above in the case of the octagram, in this case a regular polygon with the number of angles equal to the number of vertices of the polygram can be inscribed in the angle between the rays of the regular polygram. In this case, the sum of the angles of two polygons and the ray of the polygram to which they are adjacent, in the case of n> 8, will exceed 2π, in the case of n <8, will be less than 2π. In the first case, it will not be possible to build something interesting at the moment, and in the second case something else can be entered in the remaining space. This may be another polygon or a ray of a polygram.
If it is the third polygon, then the number of sides can be calculated by the equation:
π - 4π / n + 3 (π - 2π / n) = 2π
2π - 10π / n = 0
n = 5
Thus, around the ray of a five-pointed star, you can draw three pentagons with a common vertex at the top of the pentagram. Unfortunately, in this case, the mosaic will not work, except that a pattern similar to that described above, where three pentagons are grouped around the vertex of each ray:

Considering the case of two polygons and two rays, you can come to the following equation:
2 (π - 4π / n) + 2 (π - 2π / n) = 2π
2π - 12π / n = 0
n = 6
The result is such a mosaic:

If it is the third polygon, then the number of sides can be calculated by the equation:
Thus, around the ray of a five-pointed star, you can draw three pentagons with a common vertex at the top of the pentagram. Unfortunately, in this case, the mosaic will not work, except that a pattern similar to that described above, where three pentagons are grouped around the vertex of each ray:

Considering the case of two polygons and two rays, you can come to the following equation:
The result is such a mosaic:

Source: https://habr.com/ru/post/197780/
All Articles