Paradoxes of set theory and their philosophical interpretation

Short synopsis

By education I am a theoretical physicist, but I have a good mathematical base. In the magistracy, one of the subjects was philosophy, it was necessary to choose a topic and pass a job on it. Since most of the options more than once were obmusoloeno, I decided to choose something more exotic. I do not pretend to novelty, I just managed to accumulate all / almost all available literature on this topic. Philosophers and mathematicians can throw stones at me, I will only be grateful for constructive criticism.

PS A very "dry language", but quite readable after the university program. For the most part, the definitions of paradoxes were taken from Wikipedia (simplified wording and finished TeX-markup).

Introduction

Both the theory of sets and the inherent paradoxes appeared not so long ago, a little more than a hundred years ago. However, a long way was covered during this period, one way or another, set theory actually became the basis of most branches of mathematics. Its paradoxes related to the infinity of Cantor have been successfully explained in literally half a century.
')
It should start with the definition.

What is the set? The question is quite simple, the answer is quite intuitive. A set is a certain set of elements represented by a single object. Cantor in his work Beiträge zur Begründung der transfiniten Mengenlehre defines: by “set” we mean to combine into a certain whole M certain well-defined objects m of our contemplation or our thinking (which will be called “elements” of the set M) [1]. As we see, the essence has not changed, the difference is only in the part that depends on the worldview of the decisive one. The history of the theory of sets, both in logic and in mathematics, is very contradictory. In fact, Kantor started it in the XIX century, then Russell and the rest continued their work.

Paradoxes (of logic and set theory) - (Greek 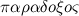- unexpected) - formal-logical contradictions that arise in the content sets of theory and formal logic while maintaining the logical correctness of the reasoning. Paradoxes arise when two mutually exclusive (contradictory) judgments are equally provable. Paradoxes can appear both within scientific theory and in ordinary reasoning (for example, Russell cites the paraphrase of his paradox about the multitude of all normal sets: “The village barber shaves all those and only those of his village who do not shave themselves. Should he shave yourself? ”). Since a formal-logical contradiction destroys reasoning as a means of detecting and proving truth (in theory, in which a paradox appears, any, both true and false, provable) is provable, the problem of identifying the sources of such contradictions and finding ways to eliminate them arises. The problem of philosophical understanding of specific solutions of paradoxes is one of the important methodological problems of formal logic and the logical foundations of mathematics.

The aim of this work is to study the paradoxes of the theory of sets as heirs of ancient antinomies and quite logical consequences of the transition to a new level of abstraction - infinity. The task is to consider the main paradoxes, their philosophical interpretation.

The main paradoxes of set theory

The barber shaves only those people who do not shave themselves. Does he shave himself?

We continue with a brief insight into the history.

Some of the logical paradoxes were known from ancient times, but due to the fact that the mathematical theory was limited to only arithmetic and geometry, it was impossible to relate them to the theory of sets. In the XIX century, the situation changed radically: Kantor in his works reached a new level of abstraction. He introduced the concept of infinity, thereby creating a new branch of mathematics and thus allowing to compare various infinities using the concept of “power of a set” [2]. However, by doing so, he spawned many paradoxes. The very first is the so-called Burali-Forti paradox . In the mathematical literature there are various formulations based on different terminology and the intended set of known theorems. Here is one of the formal definitions.

It can be proved that if x is an arbitrary set of ordinal numbers, then the set-sum there is an ordinal number greater than or equal to each of the elements x . Suppose now that - the set of all ordinal numbers. Then 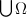- ordinal number greater than or equal to any of the numbers in . But then - ordinal number, and already strictly greater, and therefore not equal to any of the numbers in . But this contradicts the condition that - the set of all ordinal numbers.

The essence of the paradox is that when a set of all ordinal numbers is formed, a new ordinal type is formed, which was not yet among “all” transfinite ordinal numbers that existed before the formation of the set of all ordinal numbers. This paradox was discovered by Cantor himself, independently discovered and published by the Italian mathematician Burali-Forti, while the latter’s errors were corrected by Russell, after which the wording took on a final form [2, 3].

Among all attempts to avoid such paradoxes and to some extent try to explain them, the idea of ​​the already mentioned Russell deserves the most attention. He proposed to exclude from mathematics and logic impredicative sentences, in which the definition of the element of a set depends on the latter, which causes paradoxes. The rule is: “no set C can contain elements m, defined only in terms of set C, as well as elements n, suggesting this set in its definition” [4]. Such a restriction on the definition of a set makes it possible to avoid paradoxes, but at the same time it considerably narrows the area of ​​its application in mathematics. In addition, this is not enough to explain their nature and the reasons for their appearance, rooted in the dichotomy of thinking and language, in the peculiarities of formal logic [4]. To some extent, this restriction can be traced to the analogy with the fact that in a later period, cognitive psychologists and linguists began to call the “categorization of the main level”: the definition is reduced to the most easy-to-understand and study concept.

Further, Kantor in 1899 discovered a paradox named after him .

Suppose that the set of all sets exists. In this case, fair 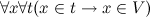, that is, every set t is a subset of V. But it follows from this 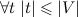- the power of any set does not exceed the power of V. But by the axiom of the set of all subsets, for V, like any set, there is a set of all subsets 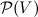and by the Cantor theorem 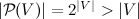that contradicts the previous statement. Therefore, V cannot exist, which contradicts the “naive” hypothesis that any syntactically correct logical condition defines a set, that is, that 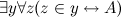for any formula A containing no y is free. A remarkable proof of the absence of such contradictions on the basis of the axiomatized theory of Zermelo-Fraenkel sets is given by Potter [3].

Both of the above paradoxes from a logical point of view are identical to “Liar” or “Bradobreyu”: the expressed judgment is drawn not only to something objective in relation to it, but also to itself. However, one should pay attention not only to the logical side, but also to the concept of infinity, which is here. The literature refers to the work of Poincare, in which he writes: “Belief in the existence of actual infinity ... makes necessary these non-predicative definitions” [2].
In general, there are some highlights [2]:

• these paradoxes violate the rule of clearly separating the “spheres” of the predicate and the subject; the degree of confusion is close to replacing one concept with another;
• usually in logic it is assumed that in the process of reasoning, the subject and the predicate retain their volume and content, in this case, there is
  the transition from one category to another, which results in a discrepancy;
• the presence of the word “all” makes sense for a finite number of elements; in the case of an infinite number of them, it is possible that
  to define itself will require the definition of the set;
• basic logical laws are violated:
  
  • the law of identity is violated when the non-identity of the subject and the predicate is revealed;
  • the law of contradiction - when two conflicting judgments are derived with the same right;
  • the law of the excluded middle - when this third has to be recognized, and not excluded, since neither the first nor the second can be recognized one without the other, since they turn out to be equally valid.
  
  

The third paradox is named after Russell . One of the definitions is given below.
Let K be the set of all sets that do not contain themselves as their element. Does K contain itself as an element? If yes, then, by definition, K, it should not be an element of K - a contradiction. If not, then, by definition, K, it should be an element of K - again, a contradiction. This statement is logically derived from Cantor's paradox, which shows their relationship. However, the philosophical essence is manifested more clearly, since the "self-movement" of the concepts occurs directly "before our eyes" [2].

The paradox of Tristram Shandy:
In Stern’s novel “The Life and Opinions of Tristram Shandy, a Gentleman,” the hero discovers that it took him a whole year to outline the events of the first day of his life, and another year was needed to describe the second day. In this regard, the hero complains that the material of his biography will accumulate faster than he can process it, and he can never complete it. “Now I say,” Russell objects to this, “that if he lived forever and his work would not have become to him, even if his life continued to be as eventful as at first, then no part of his biography would not remain unwritten. "
Indeed, the events of the n-th day could describe Shandy in the n-th year, and thus, in his autobiography, every day would be captured.

In other words, if life lasted forever, then it would be as many years as there are days.

Russell draws an analogy between this novel and Zeno with his tortoise. In his opinion, the solution lies in the fact that the whole is equivalent to its part at infinity. Those. only the axiom of common sense leads to a contradiction [2]. However, the solution to the problem lies in the field of pure mathematics. It is obvious that there are two sets - years and days, between the elements of which a one-to-one correspondence is established - a bijection. Then, under the condition of the protagonist's infinite life, there are two infinite equally powerful sets, which, if we consider power as a generalization of the concept of the number of elements in a set, resolves the paradox.

The Banach-Tarsky paradox (theorem) or the ball doubling paradox is a theorem in set theory, which states that a three-dimensional ball is equal to its two copies.
Two subsets of the Euclidean space are called equally-spaced, if one can be divided into a finite number of parts, move them, and make the second of them.
More precisely, two sets A and B are equally spaced if they can be represented as a finite union of disjoint subsets 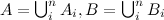so that for each i the subset 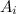congruently .

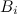If we use the choice theorem, the definition is as follows [3]:
The axiom of choice implies that there is a partition of the surface of the unit sphere into a finite number of parts that can be assembled into two spheres of unit radius by transformations of the three-dimensional Euclidean space that do not change the shape of these components.

Obviously, with the requirement for these parts to be measurable, this construction is not feasible. The famous physicist Richard Feynman in his biography told how in his time he managed to win the dispute about splitting an orange into a finite number of parts and re-arranging it [5].

At certain points, this paradox is used to refute the axiom of choice, but the problem is that what we consider elementary geometry is irrelevant. Those concepts that we consider intuitive should be extended to the level of properties of transcendental functions [3].

In order to further weaken the confidence of those who consider the axiom of choice wrong, we should mention the theorem of Mazurkevich and Sierpinski, which claims that there is a non-empty subset of the Euclidean plane, which has two non-intersecting subsets, each of which can be broken down into a finite number of parts, so they can be converted by isometry to the covering of the set E.
At the same time, the proof does not require the use of the axiom of choice [3].
Further constructions based on the axiom of certainty give resolution to the Banach-Tarsk paradox, but do not represent such interest [3].

• The paradox of Richard: you want to call "the smallest number that is not named in this book." The contradiction is that, on the one hand, this can be done, since there is the smallest number named in this book. Proceeding from it, it is possible to call the least unnamed. But here a problem arises: the continuum is uncountable, an infinite number of intermediate numbers can be inserted between any two numbers. On the other hand, if we could call this number, it would automatically be transferred from the class of those not mentioned in the book, to the class mentioned [2].
• The parade of Grelling-Nielson: words or signs can indicate a property and at the same time have it or not. The most trivial formulation is: is the word “heterologous” (which means “not applicable to itself”) heterologous? .. It is very similar to Russell's paradox due to the dialectical contradiction: the duality of form and content is violated. In the case of words with a high level of abstraction, it is impossible to decide whether these words are heterologous [2].
• The Skolem paradox: using the Gödel completeness theorem and the Löwenheim – Skolem theorem [3], we find that the axiomatic theory of sets remains true even when only a countable set of sets is supposed to be available for its interpretation. In the same time
  The axiomatic theory includes the already mentioned Cantor theorem, which leads us to uncountable infinite sets. [2]

Resolution of paradoxes

The creation of set theory gave rise to what is considered the third crisis of mathematics, which until now has not been resolved satisfactorily for all [4].
Historically, the first approach was set-theoretic. It was based on the use of actual infinity, when it was believed that any infinite sequence is complete at infinity. The idea was that in set theory it was often necessary to operate with sets that could be parts of other, more extensive sets. Successful actions in this case were possible only in one case: the data sets (finite and infinite) completed. A definite success was obvious: the axiomatic theory of Zermelo-Fraenkel sets, the whole school of mathematics by Nicolas Bourbaki, which has existed for more than half a century and is still a lot of criticism.

Logicism was an attempt to reduce all known mathematics to the terms of arithmetic, and then to reduce the terms of arithmetic to the concepts of mathematical logic. Frege did so closely, but after finishing work on labor, he was forced to indicate his inconsistency, after Russell pointed out contradictions in theory. The same Russell, as mentioned earlier, tried to exclude the use of impredicative definitions using the “theory of types”. However, his concepts of set and infinity, as well as the axiom of reducibility, turned out to be illogical. The main problem was that the qualitative differences between formal and mathematical logic were not taken into account, as well as the presence of superfluous concepts, including those of an intuitive nature.
As a result, the theory of logicism could not eliminate the dialectical contradictions of the paradoxes associated with infinity. There were only principles and methods that allowed to get rid of at least non-predicative definitions. In his discourse, Russell was Cantor's heir. [2]

In the late XIX - early XX century. the spread of the formalist point of view on mathematics was associated with the development of the axiomatic method and the program of substantiation of mathematics, which was proposed by D. Hilbert. The degree of importance of this fact is indicated by the fact that the first problem out of twenty-three, which he posed before the mathematical community, was the problem of infinity. Formalization was necessary to prove the consistency of classical mathematics, “while excluding all metaphysics from it”. Considering the means and methods used by Hilbert, his goal turned out to be fundamentally impossible, but his program had a great influence on the subsequent development of the foundations of mathematics. Hilbert worked on this problem for quite a long time, having built originally the axiomatics of geometry. Since the solution of the problem turned out to be quite successful, he decided to apply the axiomatic method to the theory of natural numbers. Here is what he wrote in connection with this: “I am pursuing an important goal: I would like to do away with the issues of substantiating mathematics as such, turning every mathematical statement into a strictly deducible formula.” It was planned to get rid of infinity by reducing it to some finite the number of operations. For this, he turned to physics with its atomism, in order to show all the inconsistency of infinite quantities. In fact, Hilbert raised the question of the relationship between theory and objective reality.

A student of Hilbert J. Herbrand gives a more or less complete picture of finite methods. By finite reasoning he understands such reasoning that satisfies the following conditions: logical paradoxes "- only a finite and definite number of objects and functions are considered;

- functions have an exact definition, and this definition allows us to calculate their value;

- the “This object exists” is never asserted if the method of its construction is not known;

- the set of all items X of an infinite collection is never considered;

- if it is known that any reasoning or theorem is true for all these X, this means that this general reasoning can be repeated for each particular X, and this general reasoning itself should be considered only as a model for such specific reasoning. "

However, at the time of the last publication in this area, Gödel had already obtained his results, in essence, he again discovered and approved the presence of dialectics in the process of knowledge. In essence, the further development of mathematics has demonstrated the inconsistency of the Hubert program.

What did Godel actually prove? There are three main results:

1. Godel showed the impossibility of mathematical proof of the consistency of any system, sufficiently extensive to include all arithmetic, evidence that would not use any other derivation rules, except those that exist in the system itself. Such evidence, which uses a more powerful derivation rule, may be useful. But if these rules of inference are stronger than the logical means of arithmetic calculus, then there will be no confidence in the consistency of the assumptions used in the proof. In any case, if the methods used are not finitist, then the Hubert program will be impracticable. Godel just shows the failure of calculations to find a finitist proof of the consistency of arithmetic.
2. Godel pointed out the fundamental limitations of the axiomatic method: the Principia Mathematica system, like any other system with which arithmetic is built, is substantially incomplete, that is, for any consistent system of arithmetic axioms there are true arithmetic sentences that are not derived from the axioms this system.
3. Gödel's theorem shows that no expansion of an arithmetic system can make it complete, and even if we fill it with an infinite set of axioms, then in the new system there will always be true, but not deducible, means of this system.The axiomatic approach to the arithmetic of natural numbers not able to cover the whole area of ​​true arithmetic judgments, and what we understand by the process of mathematical proof, does not boil down to using the axiomatic method. After Godel's theorem, it became senseless to expect that the concept of convincing mathematical proof can be given once and for all outlined forms. [2,4,6]

The last in this series of attempts to explain the theory of sets was intuitionism.

— , , . , . , ( , , , .). (, ) . , , — . , () . — , . , , , , , , . , , .

, . . , , , , , . , . , . , , .. . — , , .

, . ( ) . () () .. (). . . . , . , . . , , , . , ? ( ) , , . , , . , , . . . , , :

1) ;
2) . , , , , , , , , . , , , .

For the intuitionist Brauer as a representative of mathematical empiricism, logic is secondary, he criticizes it and the law of the excluded middle.

In his partly mystical works, he does not deny the existence of infinity, but does not allow its actualization, only potentialization. The main thing for him is the interpretation and justification of practically used logical means and mathematical reasoning. The restriction adopted by intuitionists overcomes the uncertainty of using the concept of infinity in mathematics and expresses a desire to overcome the crisis at the base of mathematics.

(.. , .. .) — , , , , , . . « » , , . . , , , , (, ). , , — , , .

, , . () . : ; ( .. ) ( ) , ; . () — , .

, , .. , . , , - , , . .. , . , , , — . , , , .. : , , . , , . .

Findings. , XIX-XX . , . , - , — , , «» , - , , , , , , . , . — , . , , , , — , , ; , , , . , , , — () , , , ; - - , - «-» .

An important point is also intuition in cognition and, in particular, in the formation of mathematical concepts. Again, there is a struggle with philosophy, attempts to exclude the law of the excluded middle, as having no meaning in mathematics and coming into it from philosophy. However, the presence of an excessive emphasis on intuition and the absence of clear mathematical justifications did not allow math to be transferred to a solid foundation. [2,4,7]

However, after the strict notion of algorithm appeared in the 1930s, mathematical constructivism took over the baton from intuitionism, whose representatives made a considerable contribution to modern computability theory. In addition, in the 1970s and 1980s, significant links emerged between some intuitionist ideas (even those that previously seemed absurd) and the mathematical theory of topohs. The mathematics available in some topos is very similar to the one that the intuitionists tried to create.

As a result, one can make a statement: most of the above paradoxes simply do not exist in set theory with self-belonging [8]. Whether such an approach is final is a controversial issue, further work in this area will be shown.

Conclusion

- , , ( ) , , () , , () (), . . .

Is the third crisis of mathematics finished (because it was in causal connection with paradoxes; now paradoxes are an integral part) - opinions diverge here, although formally known paradoxes were eliminated by 1907. However, now in mathematics there are other circumstances that can be considered either crisis, or foreshadowing a crisis (for example), the lack of a rigorous context of the continual integral).

, , ( ) , ( . ). , , , , , 1963 . , , [9].

Literature

1. Georg Cantor. Beiträge zur begründung der transfiniten mengenlehre. Mathematische Annalen, 46:481--512, 1895.
2. .. . . , 1976.
3. MD Potter. Set theory and its philosophy: a critical introduction. Oxford University Press, Incorporated, 2004.
4. .. . .: , 1990.
5. .., . . , , , !: , . . , 2008.
6. . . . . . - , (3):279--299, 2005.
7. . . . . , (4), 2006.
8. .. ( ). . . -. – , 2012.
9. . . . '' ''. , 2012.
10. .., .. . , 1976.
11. . , , : . -, 2001.
12. .., . . «», 1976.
13. YES. . . , 57(3):369--384, 1944.