CFD 3D: a simple water simulator

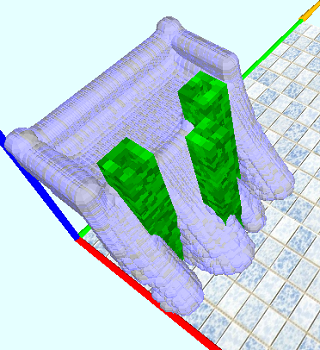Introduction

CFD (Computational fluid dynamics) - computational fluid dynamics.
It is used to simulate different processes in liquids, as well as different types of liquids (for example, honey, oil is all liquids).

In this post we consider a 2D simulator of ordinary water with an open surface and obstacles (for the 3D version, everything is the same as + source codes are available).
The surface of the water is a boundary separating the water from the air. This allows you to simulate waves, falling drops, etc.

I decided to write my simulator for several reasons. One of them is the lack of normally written source codes on this topic on the Internet. All that I found was either on Fortran, or only 2d, or it was written very difficult to understand.
')
So, the main features of the simulator:

• real-time mode
• simple and clear calculation scheme + explicit, implicit
• open source
• there are both 2d and 3d
• built-in simple opengl render
• xml scene description

In terms of calculations, I pushed away from the Navier-Stokes equations (as well as from the sources found in the internet).
This is a system of partial differential equations describing the motion of a viscous incompressible fluid. The word incompressible here is rather a tick, since all liquids are by definition incompressible. Viscosity refers to friction between individual particles, it does not allow them to scatter in different directions, as is the case with gas, when it fills all the volume allocated to it. Particles of a liquid try to keep together whenever possible.

In my simulator, I used a slightly modified set of equations, more on that below ...

Hydrodynamic equations

So, here are the basic Navier-Stokes equations in general (vector) form:

Here:

• u is the traditional designation of the velocity field (in 2D, the speed consists of 2 components in x and in y directions - they are designated respectively as u and v)
  
• p is the pressure
• t - time
• the symbol rho is the density of the fluid
• nu symbol - kinematic viscosity coefficient
• Fext - any external forces acting on the fluid, such as gravity (g)

The first of the equations is the equation of motion, the second is the continuity equation.
The equation of motion looks like Newton's equation ma = F, where we have on the right - the sum of the forces acting on the fluid is pressure, diffusion, gravity ...

For the 2D version of the equation take the form (here they are already presented in a dimensionless form):



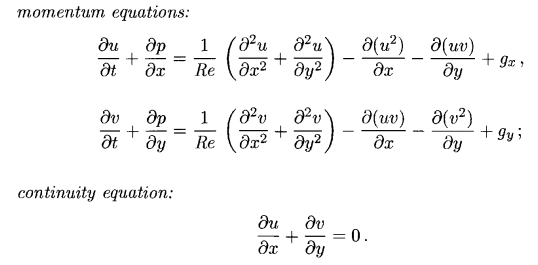
The motion equation is now represented by 2 equations - for 2 speed components - u and v.
Regarding the new coefficient, Re is the Reynolds number (it turned out in the transition to dimensionless variables), which replaces 2 previous coefficients at once — coeff. density and viscosity. It depends on him what water will be like - honey or ordinary water. The more Re the more liquid is like ordinary water.
In parentheses, this is our expression that defines the viscous behavior of a fluid (or diffusion). The remaining members on the right side (except gravity) are convection. In the left side - the speed and pressure.

Next, I slightly simplified these equations:



As you can see, convection has disappeared, which slightly impairs the behavior of the liquid, but overall it looks visually quite normal. The absence of convection gives several advantages at once — the non-linearity disappears, stability improves and the time step can be made longer, and convection is usually a very expensive term in terms of the necessary calculations. , besides, in order to correctly discretize convection, special schemes are used - which looks rather cumbersome.

When solving equations, a special scheme is used, called Splitting. I would like to dwell on this in more detail, but this is more likely for a separate post. The topic is quite large. It is very well described in the book
Bridson R. Fluid Simulation for Computer Graphics.pdf in the Overview of numerical simulation section.
And here Numerical simulation in fluid dynamics Griebel M Dornseifer T Neunhoeffer T SIAM 1998

Here is the split equation scheme:



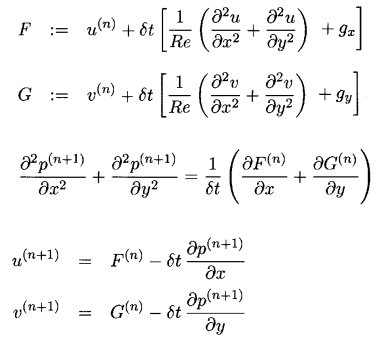
For the time step, the Euler method is used. Also, at the first step, we lower the pressure and get an intermediate calculation of the speeds F and G. These speeds, besides not taking the pressure into account, will not yet satisfy the continuity equation. By cunning manipulation, an equation is found for calculating pressure, which also solves the problem with the continuity equation. Solving this equation using the already calculated F and G we find the new pressure P.
Further, at the 3rd step, the velocity correction takes into account the calculated pressure.
This completes one full time step and at the next step everything repeats again.

Discretization of equations

For discretization of equations, the finite difference method is used. For the time step, the standard Euler method is used - it looks schematically like this: u (n + 1) = u (n) + dt * f,
where f means the whole part of the equation which does not include the time differential.

In general, the value of speed at a new time (u (n + 1)) is found from the value at the previous time (u (n)).
I will not describe the discrete analogues of the equations in this post. This is very well done in the book “Numerical simulation in fluid dynamics” (Griebel M Dornseifer T Neunhoeffer T SIAM 1998).

To solve discrete equations, a non-matrix method of solving is used, but an iterative one - Gauss-Seidel. It does not require pre-assembly of matrices and does not require any intermediate arrays at all, makes it easy to modify the design scheme, the approximate solution is already after 1 iteration - which greatly speeds up the whole simulation.

In this post we will consider the 2D case, the main focus will be on explaining the boundary conditions, since they cause the greatest difficulties in solving equations. The entire simulated area is divided into imax points horizontally and jmax vertically. It turns out the grid imax * jmax cells.
To them from 4 borders are added boundary points. The total is an array of size (imax + 2) * (jmax + 2).

Each cell has its own velocity and pressure values ​​- it’s customary to talk about the velocity vector field and the scalar pressure field on the computational grid.
U is the velocity of a particle in a cell in x
V is the particle velocity in the cell along y
P - pressure

It is usually customary to place the calculated variables (U, V, P) in the center of the cells, but in the case of fluid modeling this always causes problems with the solution — it turns out to be not entirely correct and oscillating. Therefore, CFD uses an exploded grid (staggered grid) - it is also called leapfrog.



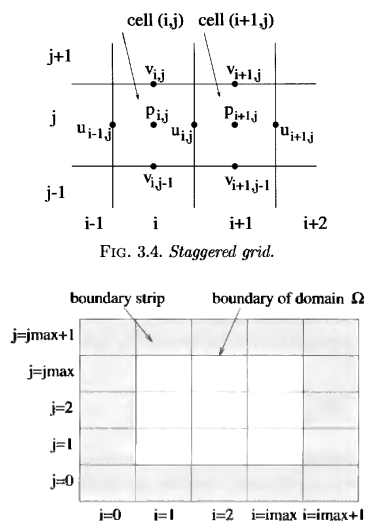
It can be seen from the figure that the speeds are not in the cell itself but on its faces, u is on the right border of the cell, and v is on the upper border.

Boundary conditions on the walls

For the calculation by the finite difference method, we need to set the values ​​(u, v, p) at the boundaries of the computational grid. These are 4 walls - on the left, right, below and above. The boundary conditions can be of types no-slip and free-sleep; There are other types, but these are more specialized conditions than general ones.

free-sleep - this means that the fluid slides freely along the wall, as if there is no friction and nothing prevents it from moving along it.
In this post we do not consider this type of boundary conditions.

no-slip is a sticking condition - that is, the liquid slows down when it hits a wall.
This means that the velocity of the fluid coincides with the velocity of the wall (that is, in our case it is equal to zero on the fixed boundary).

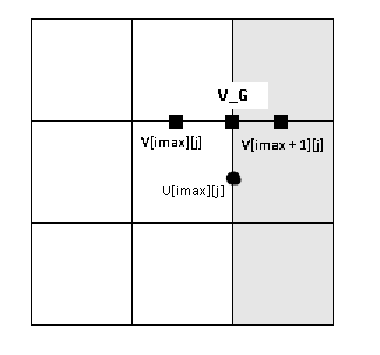
Consider, for example, only the right boundary: the velocity component u = 0, since it is perpendicular to the wall and water should not penetrate the boundary.
The v component for the no-slip border case is also 0, but for our staggered grid it will have to be adjusted. For the v component, given that v is not right on the border, you need to correct the expression a little.
v on the wall will be equal to the average between the 2 nd last cells. v_g = (v [imax + 1] [j] + v [imax] [j]) / 2
v_g equate zero ((v [imax + 1] [j] + v [imax] [j]) / 2 = 0) and find the value v [imax + 1] [j], which we need to specify in the program:
v [imax + 1] [j] = - v [imax] [j];
The same must be done for u components at the upper boundary.



4 borders are represented in the array with the following coordinates:

left wall

u [0] [j], where j runs through the whole wall
v [0] [j]

Here is how it looks in code:

for (j = 0; j <= jmax + 1; j++) { U[0][j] = 0.0; V[0][j] = -V[1][j]; } 

bottom wall

u [i] [0]
v [i] [0]

 for (i = 0; i <= imax + 1; i++) { U[i][0] = -U[i][1]; V[i][0] = 0.0; } 

right wall
Because we have a spaced grid, then on the right wall we have a border for the values ​​of u that do not pass along the last column but on the penultimate one — therefore, we set the values ​​for U in the cell - U [imax] [j].

u [imax] [j]
v [imax + 1] [j]

 for (j = 0; j <= jmax + 1; j++) { U[imax][j] = 0.0; V[imax + 1][j] = -V[imax][j]; } 

upper wall
Here, for values ​​of v, the boundary passes along the penultimate line - jmax - therefore, we set the values ​​for V in the cell - V [i] [jmax]

u [i] [jmax + 1]
v [i] [jmax]

 for (i = 0; i <= imax + 1; i++) { U[i][jmax + 1] = -U[i][jmax]; V[i][jmax] = 0.0; } 

To test the basic solver, all boundary values ​​can be set = 0.

We also need to put pressure on the borders. The pressure is set at the center of the cells and not at the edges as speed. Therefore, everything is very simple with it. The pressure at the borders can be set the same as in the neighboring cells. Just copy the values ​​from the neighboring cells.

 for (j = 1; j <= jmax; j++) { //   P[0][j] = P[1][j]; //   P[imax + 1][j] = P[imax][j]; } for (i = 1; i <= imax; i++) { P[i][0] = P[i][1]; P[i][jmax + 1] = P[i][jmax]; } 

Boundary conditions on obstacles

Obstacles are represented by the C_B flag. The boundary conditions for them are set on the same principle as for the external walls. I will give 2 examples of pressure setting:

 if (IsObstacle(i, j)) { //     -  -    P   if (IsFluid(i, j - 1)) { P[i][j] = P[i][j - 1]; } //   -  ... else if (IsFluid(i - 1, j)) { P[i][j] = P[i - 1][j]; } // ....... } 

For an angular cell, we take the average of the values ​​of the water cells surrounding it. For example, let's take an obstacle; there will be water on the left and on top of it. Then we consider the pressure in the obstacle cell as:

 if (IsFluid(i - 1, j) && IsFluid(i, j + 1)) { P[i][j] = (P[i][j + 1] + P[i - 1][j]) / 2; } 

Surface boundary conditions

The surface and its movement is modeled with particles. (Sources with boundary conditions on the surface, made as described in this section are in the folder simpletestobstacle.)

Initially, the particles are placed in cells with liquid, 4 pieces per cell (1 next to each corner). Then the particles at each step are moved using the simple Euler method from classical mechanics. The speeds for movement are taken in each cell as average across the entire cell (although it is not a problem to use, for example, interpolation).

  x = particles[k].x; y = particles[k].y; //        i = (int)(x / delx); j = (int)(y / dely); u = U[i][j]; v = V[i][j]; //        x += delt * u; y += delt * v; 

At each step, the cells with particles are labeled as water. The rest are empty cells, in which the calculation of the main variables (u, v, p) is not performed.

To calculate the main variables, it is necessary to set the boundary conditions on the surface and adjacent cells, as well as it was required for the walls. But first you need to determine which cells, from those labeled as water, belong to the surface, and also from which side the air is located. For this purpose, 2 arrays are used - FLAG and FLAGSURF. In the first, only cell types are specified - water, air (empty) and obstacles. Here are the corresponding flags (abbreviations B - boundary F - fluid E - empty):

 public const int C_B = 0x0000; // public const int C_F = 0x0010;// public const int C_E = 0x1000;// 

The FLAGSURF array is used to determine surface cells, for other cells the value there is = 0. Flags in this array determine not only the cell type, but also all combinations of neighboring cells in which it is empty. Flags are made as standard bit masks so that they can be combined.
Each value in FLAGSURF contains 4 bits that correspond to 4 sides (adjacent cells).
If the bit is set to 1, then in the corresponding adjacent cell it is empty. If 0, then there is water.
Bit location: 0000 NSWO 0000 0000 - the letters denote the 4 sides N (North north) S (South south) W (West east) and O (west).

The entire list of flags is in the source, so I’ll give just some examples of the values:

public const int C_W = 0x0200; // 512
in binary form, the value looks like this 0000 0010 0000 0000
Here the flag corresponding to the side W is set to 1. This means that to the left of the current cell is empty.
At the same time, the remaining 3 bits are set to 0 - it means the remaining neighboring cells are filled with water.



public const int C_SW = 0x0600; // 1536 0000 0110 0000 0000
Here the flag corresponding to the sides of W and S is set to 1. This means that to the left and below of the current cell is empty, and the remaining cells are aquatic.



When determining the types of surface cells and filling in the FLAGSURF array, the corresponding bits are set to 1 thus:

 //   ,      1 if (FLAG[i-1][j] == GG.C_E) FLAGSURF[i][j] = FLAGSURF[i][j] | GG.C_W; 

The FLAGSURF array is mainly needed only for the convenience of setting the boundary conditions on the surface. Since for different types of surface cells apply different boundary conditions. As already mentioned, we need to put the boundary conditions in the empty cells that are near the surface cells and also the boundary conditions are needed in the surface cells themselves, since we have a staggered grid and not all surface cells are included in the calculation of the uv variables.

The principle of setting values ​​is simple. Since the air pressure is 1000 times less than the pressure in water - then they can be neglected and allow water to move freely along the surface, without limiting its speed in any way or changing the direction of movement. Of course, my scheme does not take into account surface tension, otherwise everything would be much more complicated.

We affix the values ​​of the velocities U and V in the superficial cells and the empty cells bordering on them, while not forgetting that we have a staggered grid.
Values ​​for prostanovki taken from neighboring water cells. It only remained to decide from which neighboring cells all this is taken, because there can be several such cells.



Here is a screen with the boundary conditions that need to be put down. The blue squares are water. Black marks - required boundary conditions. Note that the tags are located partly in the surface cells and partly in the empty cells. This happens because we have such conditions in the solver code (as you can see, UV is not calculated in the cells in front of the right boundary wall):

  if (IsFluid(i, j) && IsFluid(i+1, j)){ F[i][j] = ... } 

Consider a few examples:

cage with flag C_SW

  case GG.C_SW: { U[i][j - 1] = U[i][j]; V[i][j - 1] = V[i][j]; U[i - 1][j] = U[i][j]; V[i - 1][j] = V[i][j]; } break; 

Here, the values ​​in the cell itself are not needed - they will be calculated in the solver. But we need values ​​in the neighboring empty cells - because there are terms with U [i] [j - 1] in the solver, etc.

The nearest water cell to these empty cells is the cell [i] [j] from it and take the values ​​U and V.
The figure shows that the value for V [i - 1] [j] could be taken both from the cell [i] [j] and from [i - 1] [j + 1] - but in the general case, the cell [ i - 1] [j + 1] may not be water; besides, the value of V in it may also be boundary and not yet put down. Therefore, the correct version is [i] [j] because the values ​​in it will be calculated in the solver .

cage with flag C_W

  case GG.C_W: { U[i - 1][j] = U[i][j]; V[i - 1][j] = V[i][j]; } break; 

Here everything is similar.

cage with flag C_NW

  case GG.C_NW: { V[i][j] = V[i][j - 1]; U[i - 1][j] = U[i][j]; } break; 

Here, the value of U in the cell itself will be calculated in the solver, since to her right there is a water cell. But V must be stamped, since the cell on top is empty. It is also necessary to set the value U [i - 1] [j], and TK when calculating U [i] [j], the values ​​will also be required in the cells next to it, including U [i - 1] [j].

Just as in the previous case, the value of V [i] [j] is taken from the cell V [i] [j - 1], and not from V [i-1] [j] - the value in V [i-1 ] [j] may be boundary and not yet known.

Set the pressure in empty cells and surface cells = 0. This is not entirely correct, but it works.
In surface cells, pressure is needed, because when solving the equation for pressure, these cells are boundary and in them pressure is not calculated directly.

Algorithm of fluid motion using particles only on the surface

The source contains variants named track in the title. This is a method of moving a free surface in which particles move only on the surface itself, and not in the entire volume of the liquid. This is somewhat similar to the VOF method - but a preliminary surface reconstruction is being done there, which is quite cumbersome. In my method, if a particle leaves the cell, it is marked empty, and in the nearby cells of the fluid in which there are no particles, particles are added to know where the surface is. If the particle goes into an empty cell, then the cell is labeled as liquid. Of course, this method has a decent amount of inaccuracy, but it is fast and does not require complicated coding.

Implicit calculation scheme

There is also an implicit version of the solver in the source code - it applies to equations for speeds, the differences in the code from the explicit version are minimal. With discretization, all the terms with U and V [i] [j] simply go to the left side of the equation and not to the right, as in an explicit.Implicit (implicit) scheme allows for much larger time steps, which is impossible in the case of explicit.
About implicit you can read here http://math.mit.edu/cse/codes/mit18086_navierstokes.pdf .

3D version

In the 3D version, everything is done by analogy with 2D.
Key management F1-F8 + WASD, arrows and ER PgUp PgDown to rotate the camera.
For scenes with a water source - the P key - to enable water pressure off.
G - better surface rendering (spheres are used instead of cubes), but it terribly slows down.
In the Demos folder - there are scenes and parameters (dimensions, time step, gravity and number of particles per cell) as an xml file. It is also possible to paint your HeightMap (height map) in paint, any sizes can be - there is autoresize.

In conclusion, I will give screenshots from 2D and 3D:







Source codes are here sourceforge .





PS If there are people familiar with CFD, it would be interesting to improve the project together in terms of speed and correctness of the solution (especially when modeling the surface).
Rendering myself I can gash more or less, but math and physics is not my main direction. I will welcome any comments and helpful advice.