I know that you know, that I know that you know ...
Free translation of one of the answers from mathoverflow . The answer, in principle, is so self-sufficient and interesting that it can be read without understanding the essence of the question. Therefore, if for any reason you are stalled while reading the question, I advise you to go straight to the answer.
Sometimes in life there are situations that are described by sentences like: “I know that you know, that I know ... something”. Imagine that you baked a cherry pie and put it to cool on the windowsill, and I ate it quietly. Here is a list of more and more complex sentences that bring us closer and closer to full knowledge of what is happening. For example,
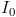: “I know that you baked a cake and put it to cool on the window sill; but you do not know what I know. ” In that case, if I eat a cake, then most likely no one will know about it.
')
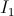: “I know that you baked a cake and put it to cool on the window sill; you know that I know; but I don't know what you know, what I know. ” If I eat a cake, it can lead to a rather delicate situation for me.
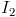: “I know that you baked a cake and put it to cool on the window sill; you know that I know; I know that you know that I know; but you don't know what I know. that you know that I know. " In that case, after I eat the cake, I’ll have hope to turn the situation around so that you don’t know about my crime.
...
For small values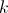
I can still imagine how to go from a sentence 
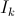to 
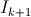really changing the essence of what is happening. But I absolutely cannot imagine how, say, the transition from 
to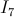 
may affect my strategy after I eat the cake.
Are there any situations in life, whether real or artificial, where the transition from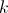 to 
for large values 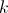can really influence the strategy of action? And what's about 
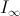? How are such situations modeled in mathematics?
My wife and I have an agreement that I always take our son Horace from school, and she takes our daughter Hypatia. One day it so happened that, knowing that I would pass close to my daughter's school, I wrote an email to my wife: “Today I will take Hypatia, and you take Horace. Please confirm that you have read the message. Otherwise, we act as usual. ” My wife responded by text message: “OK, let's do it, but confirm that you read the message so that I know for sure that we are really changing.” Then I left a voice message to her: “Yes, we definitely change as soon as I know that you received this message.” Then she wrote me an email: “I received your message. We are changing. But let me know that you read my letter so that I can count on you. ” You see, without confirmation, she could not be sure that I received confirmation of her confirmation of my first message. Without it, she could conclude that the plan to swap responsibilities would have to be canceled. And so on to infinity ...
It was a shame to us that at no stage of our “conversation” could we be sure that the second of us had all the necessary information to follow the plan I proposed. As a result, due to the fact that we had the opportunity to exchange only a finite number of messages, we made the decision to refuse the proposal to exchange duties. Both of us independently from each other came to this, the only correct, decision.
Indeed, my first message required confirmation, so that the plan I proposed could take effect. Moreover, if we for a moment imagine that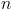
-th message does not require confirmation, then it immediately follows that it does not matter whether it is read or not. So it does not need to send. By induction, we get that no amount of evidence is enough to embody my plan.
PS Additionally, you can see the task of two generals .
This example is, in fact, very deep. It works for the case of a normal conversation. Strictly speaking, they could not even agree, even if they were standing side by side and would have spoken out loud to each other. Instead of "... confirm that you received the message" they would ask: "... confirm that you heard me (a)".
Question
Sometimes in life there are situations that are described by sentences like: “I know that you know, that I know ... something”. Imagine that you baked a cherry pie and put it to cool on the windowsill, and I ate it quietly. Here is a list of more and more complex sentences that bring us closer and closer to full knowledge of what is happening. For example,
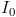: “I know that you baked a cake and put it to cool on the window sill; but you do not know what I know. ” In that case, if I eat a cake, then most likely no one will know about it.')
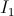: “I know that you baked a cake and put it to cool on the window sill; you know that I know; but I don't know what you know, what I know. ” If I eat a cake, it can lead to a rather delicate situation for me. 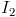: “I know that you baked a cake and put it to cool on the window sill; you know that I know; I know that you know that I know; but you don't know what I know. that you know that I know. " In that case, after I eat the cake, I’ll have hope to turn the situation around so that you don’t know about my crime....
For small values
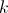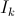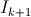I can still imagine how to go from a sentence to really changing the essence of what is happening. But I absolutely cannot imagine how, say, the transition from to 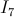may affect my strategy after I eat the cake.Are there any situations in life, whether real or artificial, where the transition from
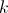to for large values 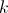can really influence the strategy of action? And what's about 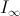? How are such situations modeled in mathematics?Answer
My wife and I have an agreement that I always take our son Horace from school, and she takes our daughter Hypatia. One day it so happened that, knowing that I would pass close to my daughter's school, I wrote an email to my wife: “Today I will take Hypatia, and you take Horace. Please confirm that you have read the message. Otherwise, we act as usual. ” My wife responded by text message: “OK, let's do it, but confirm that you read the message so that I know for sure that we are really changing.” Then I left a voice message to her: “Yes, we definitely change as soon as I know that you received this message.” Then she wrote me an email: “I received your message. We are changing. But let me know that you read my letter so that I can count on you. ” You see, without confirmation, she could not be sure that I received confirmation of her confirmation of my first message. Without it, she could conclude that the plan to swap responsibilities would have to be canceled. And so on to infinity ...
It was a shame to us that at no stage of our “conversation” could we be sure that the second of us had all the necessary information to follow the plan I proposed. As a result, due to the fact that we had the opportunity to exchange only a finite number of messages, we made the decision to refuse the proposal to exchange duties. Both of us independently from each other came to this, the only correct, decision.
Indeed, my first message required confirmation, so that the plan I proposed could take effect. Moreover, if we for a moment imagine that
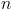-th message does not require confirmation, then it immediately follows that it does not matter whether it is read or not. So it does not need to send. By induction, we get that no amount of evidence is enough to embody my plan.PS Additionally, you can see the task of two generals .
This example is, in fact, very deep. It works for the case of a normal conversation. Strictly speaking, they could not even agree, even if they were standing side by side and would have spoken out loud to each other. Instead of "... confirm that you received the message" they would ask: "... confirm that you heard me (a)".
Source: https://habr.com/ru/post/197034/
All Articles