Topology for the smallest. Part 2
In this article, I continue my gentle introduction to topology. The first part is here .
Again, I warn you that everything you read is written twice by the humanities (bachelor and master), so you should not believe blindly. In general, you are warned.
Notes about errors (mathematical) are welcome.
Another warning - a lot of pictures.
Picture to attract attention (not related to our text).

How do you think without breaking these figures, but by deforming in any way, can they be disconnected?
Initially, I planned to talk about metric spaces in the second part, but then I decided to postpone it for the future, and now I’ll talk in more detail about the surroundings and related concepts, which I only briefly mentioned in the last part. Thus, we are somewhere in the first chapter of a book on General Topology.
The black solid outline in the figures will denote closed sets, and sets without a contour will be open. Letters ttt I will reduce then and only then.
Go.
So, the subset U of a topological space (X, T) is called a neighborhood of the point x ttt, when U contains an open set containing x

The picture above illustrates this situation. I showed the neighborhood of point x as a circle bounded by a dotted line. Of course, the surroundings don't have to be around. It only must contain the open set to which the point x belongs. In this case, I depicted the sets in red. Since every set belongs to itself, it is obvious that every open set is a neighborhood of each of its points. The reverse is not true. The neighborhood is not at all obliged to be open-minded. In the picture below, I illustrated these situations.
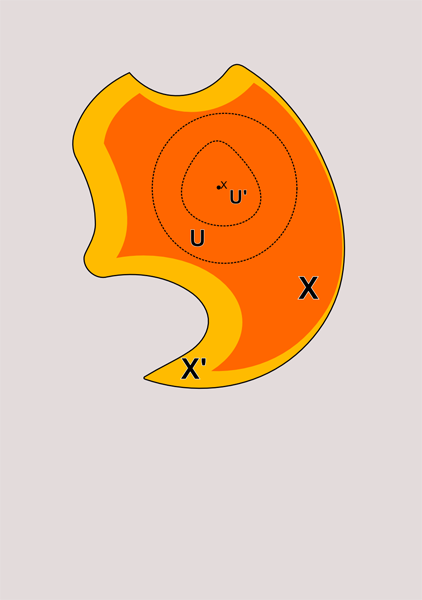
U, U 'and X and X' are neighborhoods of x. At the same time, U, U 'and X are open, but X' is not.
From all this follows a very important theorem (and perhaps not very much) - a set of open dmt, when it contains neighborhoods of all its points.
I thought for a long time how to draw it. The result was such a drawing as below.

Look at this set X. If this set is open then whatever point you find in it there will always be an neighborhood belonging to the set. I showed how it will look when you zoom in on the image. For example, the point d lies almost on the very edge, but if you look closely at this section, you can see that around it you can always describe an open circle. You can imagine such a game. Let the demon and the genius choose a random set. The demon puts on the fact that the multitude is not open, but a genius that is open. After that, the demon points out some point of the set, and the genius tries to draw a neighborhood around it. If everything works out, it gets a prize, and the demon gives a new point. If a genius is lucky with a lot, he can win a whole infinity of prizes. Of course, mortal creatures in this game is not too relevant to play.

')
There is an important type of points, which are called accumulation points or limit points.
The limit point is the point of the subset A of the topological space (X, T), in any neighborhood of which there is a point of the set A.
Phew If we talk based on visual intuition, then the limiting points are those points that lie "inside" the set or on the "edge". Not every point that belongs to a set is a limit. Look at the picture below.
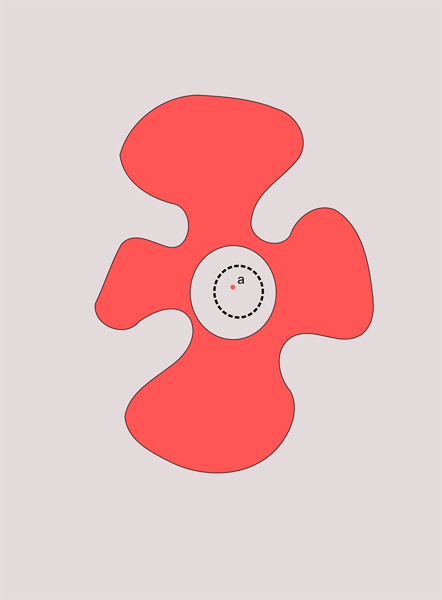
Point a belongs to the reddish set, but it has a neighborhood in which there are no other points of this set. So it is not the limit. And, conversely, there are points that may not belong to this set, but still be the limit for it.
The picture below shows different situations.
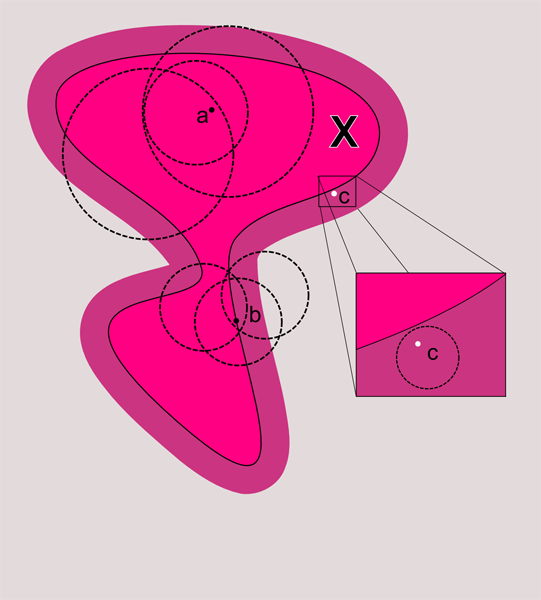
Point a contains a point X in any neighborhood. Point b is also. Therefore, they are points of accumulation. But the point c, although it has neighborhoods in which the points X are contained, but also has other neighborhoods that do not contain points from X.
The neighborhood in this case is very similar to the concept of a neighborhood in the everyday sense - to lie in a neighborhood means to be in the vicinity. In a sense, the neighborhood expresses intimacy. But it is important to understand that so far all the spaces we are talking about are not equipped with a metric, i.e. do not have a distance and we can not express intimacy numerically. Later, when we talk about metric spaces, we will return to the topic of the neighborhood again, but from a slightly different side.
All this allows us to formulate the definition of closed sets in a new language. In the last chapter I said that closed sets are those that are additions to open ones. This is a rather formal definition, but the surroundings allow you to see it in a new light, and it unexpectedly acquires depth and, as it were, new faces.
Thus, a subset of a topological space is closed when it contains all its limit points.
Look at the drawing.

We have a red set, which is a subset of the orange set. It is open, since all its points enter it with its neighborhood. And, obviously, there are an infinite number of limit points that do not belong to him. I drew a few of them in the picture in the middle. If we add to the set the set of all its limit points, then it becomes closed.
How is this proved? Well, everything is simple here. Suppose A is a subset of a topological space X. There is a point x that does not belong to A and has an open neighborhood U that does not intersect A. Since this neighborhood is open, it is a neighborhood of any of its points. Since it does not intersect A, then none of the points in this neighborhood is the limit point of A. This means that (∪set of its limit points) ∪ open U = X. Or X \ (set of its limit points) = open lots of
Those. And together with the set of its limiting points, it is an addition to the open set, and therefore is closed. It is amazing how the concept of neighborhood turned out to be deeply connected with the concept of openness and isolation.
Now we define the closure concept, which is closely related to closeness
The closure of the subset X is the intersection of all closed sets that contain X. The closure of X is denoted, for example, by [X]. The closure of a subset is a closed set, because the intersection of closed sets is closed. And it is obvious that the closure is the smallest closed set that contains X
Look at the picture.

We have a closed yellow set and an orange open. If we successively intersect all closed sets that contain orange (I showed only some steps), then we get the closure of the orange set.
I think, you guessed it, the set is closed if it coincides with its closure ([X] = X).
A closed set is a set that contains all its limit points, it is also true that a closure is the union of the set and its limit points. It seems trivial, but this fact must be proved. It is proved simply that the limit points of the set X are, obviously, the limit points of each set containing X. Therefore, they belong to each closed set containing X. Therefore, the limit points of X are contained in any intersection of these sets, i.e. in [x]. On the other hand, the set together with its limit points is closed, and therefore the closure of the set X is the set X together with its limit points.
An operator that assigns a set to its closure is called a closure operator. I will refer to it as ⊛. Usually in mathematics it is not so designated, but we after all have the right to the designations.
It has several properties:
1) ⊛∅ = ∅
This means that the closure of the empty set is empty.
2) X⊆⊛X
The set is contained in its closure.
3) ⊛X = ⊛⊛X
The closure of the closure of the set is equal to the closure of the set
4) ⊛X∪⊛X '= ⊛ (X∪X')
The union of the closures is equal to the closure of the union.
These rules are called the Kuratovsky closure axioms.
I think one of the best ways to understand topology is to look at some very small topological space. For example, one that consists of only a few elements.

Suppose we have a set {a, b, c, d, e} equipped with the topology described in the figure. Consider a subset of this set {a, b, c}. What points are limiting for him in this topology? By definition, these will be those points that have points from {a, b, c} in each of their neighborhoods besides themselves. I showed the open neighborhood schematically with the help of circles. Points inside one circle are in one neighborhood (or in one open subset of a set). Therefore, we check for each point whether it has a neighborhood in which there are no points from {a, b, c}. Point a has such a neighborhood. This is a neighborhood where there is only a point a. So it is not a limiting point. In all neighborhoods of b there are points from {a, b, c} (besides b itself). Similarly for d and e. Etc. thus, from this scheme, we see that b, d, e are limit points for {a, b, c}, but a and c are not.
We equip the same spaces with an anti-discrete topology and see what happens.

In the anti-discrete topology, each point will be the limit for the set {a, b, c} (and for any other, except the set itself and the empty set). It is not for nothing that this topology is called the topology of stuck points, in it all points of space are stuck together with each other, you can't figure out exactly where. I would not want to live in a universe with an anti-discrete topology.
In discrete topology, we have the opposite situation. I tried to draw, but to be honest, I refused this idea. You do remember how many open sets there will turn out even in a relatively small set.
Looking at all these pictures, I want to define the concept of the interior of a set and a border. For example, when I was drawing sets outlined by a black outline, I immediately wanted to call this line the border of a set. However, so far we have not had the concept of boundaries and insides. And now it will be.
A point is called an interior point of a set when the set is its neighborhood. The interior of a set is the collection of all its interior points. In other words, the interior of a set is the largest open set contained in it. Those. the set is open only when it coincides with its interior. Agree, this is very similar to the closure definition.
The interior of any subset of the anti-discrete space is empty. In a discrete space, any subset coincides with its interior and with its closure at the same time.
The boundary of a set X (X subset of A) is the set of those points of A whose neighborhood contains both points X and A / X.
I drew such a picture, a little in the style of abstract artists came out.

Here you go. on this note, I end the article. For the exercise, you can think about which points are the boundary of the set {a, b, c} from the image, which are its interior (if any), which is its closure. And, of course, is it possible to disconnect the figures from the initial picture. And how to do it (very much develops spatial thinking). I promise to attach the answer to the last question to the following articles.
All for now.
Again, I warn you that everything you read is written twice by the humanities (bachelor and master), so you should not believe blindly. In general, you are warned.
Notes about errors (mathematical) are welcome.
Another warning - a lot of pictures.
Picture to attract attention (not related to our text).

How do you think without breaking these figures, but by deforming in any way, can they be disconnected?
Initially, I planned to talk about metric spaces in the second part, but then I decided to postpone it for the future, and now I’ll talk in more detail about the surroundings and related concepts, which I only briefly mentioned in the last part. Thus, we are somewhere in the first chapter of a book on General Topology.
The black solid outline in the figures will denote closed sets, and sets without a contour will be open. Letters ttt I will reduce then and only then.
Go.
So, the subset U of a topological space (X, T) is called a neighborhood of the point x ttt, when U contains an open set containing x

The picture above illustrates this situation. I showed the neighborhood of point x as a circle bounded by a dotted line. Of course, the surroundings don't have to be around. It only must contain the open set to which the point x belongs. In this case, I depicted the sets in red. Since every set belongs to itself, it is obvious that every open set is a neighborhood of each of its points. The reverse is not true. The neighborhood is not at all obliged to be open-minded. In the picture below, I illustrated these situations.

U, U 'and X and X' are neighborhoods of x. At the same time, U, U 'and X are open, but X' is not.
From all this follows a very important theorem (and perhaps not very much) - a set of open dmt, when it contains neighborhoods of all its points.
I thought for a long time how to draw it. The result was such a drawing as below.

Look at this set X. If this set is open then whatever point you find in it there will always be an neighborhood belonging to the set. I showed how it will look when you zoom in on the image. For example, the point d lies almost on the very edge, but if you look closely at this section, you can see that around it you can always describe an open circle. You can imagine such a game. Let the demon and the genius choose a random set. The demon puts on the fact that the multitude is not open, but a genius that is open. After that, the demon points out some point of the set, and the genius tries to draw a neighborhood around it. If everything works out, it gets a prize, and the demon gives a new point. If a genius is lucky with a lot, he can win a whole infinity of prizes. Of course, mortal creatures in this game is not too relevant to play.

')
There is an important type of points, which are called accumulation points or limit points.
The limit point is the point of the subset A of the topological space (X, T), in any neighborhood of which there is a point of the set A.
Phew If we talk based on visual intuition, then the limiting points are those points that lie "inside" the set or on the "edge". Not every point that belongs to a set is a limit. Look at the picture below.

Point a belongs to the reddish set, but it has a neighborhood in which there are no other points of this set. So it is not the limit. And, conversely, there are points that may not belong to this set, but still be the limit for it.
The picture below shows different situations.

Point a contains a point X in any neighborhood. Point b is also. Therefore, they are points of accumulation. But the point c, although it has neighborhoods in which the points X are contained, but also has other neighborhoods that do not contain points from X.
The neighborhood in this case is very similar to the concept of a neighborhood in the everyday sense - to lie in a neighborhood means to be in the vicinity. In a sense, the neighborhood expresses intimacy. But it is important to understand that so far all the spaces we are talking about are not equipped with a metric, i.e. do not have a distance and we can not express intimacy numerically. Later, when we talk about metric spaces, we will return to the topic of the neighborhood again, but from a slightly different side.
All this allows us to formulate the definition of closed sets in a new language. In the last chapter I said that closed sets are those that are additions to open ones. This is a rather formal definition, but the surroundings allow you to see it in a new light, and it unexpectedly acquires depth and, as it were, new faces.
Thus, a subset of a topological space is closed when it contains all its limit points.
Look at the drawing.

We have a red set, which is a subset of the orange set. It is open, since all its points enter it with its neighborhood. And, obviously, there are an infinite number of limit points that do not belong to him. I drew a few of them in the picture in the middle. If we add to the set the set of all its limit points, then it becomes closed.
How is this proved? Well, everything is simple here. Suppose A is a subset of a topological space X. There is a point x that does not belong to A and has an open neighborhood U that does not intersect A. Since this neighborhood is open, it is a neighborhood of any of its points. Since it does not intersect A, then none of the points in this neighborhood is the limit point of A. This means that (∪set of its limit points) ∪ open U = X. Or X \ (set of its limit points) = open lots of
Those. And together with the set of its limiting points, it is an addition to the open set, and therefore is closed. It is amazing how the concept of neighborhood turned out to be deeply connected with the concept of openness and isolation.
Now we define the closure concept, which is closely related to closeness
The closure of the subset X is the intersection of all closed sets that contain X. The closure of X is denoted, for example, by [X]. The closure of a subset is a closed set, because the intersection of closed sets is closed. And it is obvious that the closure is the smallest closed set that contains X
Look at the picture.

We have a closed yellow set and an orange open. If we successively intersect all closed sets that contain orange (I showed only some steps), then we get the closure of the orange set.
I think, you guessed it, the set is closed if it coincides with its closure ([X] = X).
A closed set is a set that contains all its limit points, it is also true that a closure is the union of the set and its limit points. It seems trivial, but this fact must be proved. It is proved simply that the limit points of the set X are, obviously, the limit points of each set containing X. Therefore, they belong to each closed set containing X. Therefore, the limit points of X are contained in any intersection of these sets, i.e. in [x]. On the other hand, the set together with its limit points is closed, and therefore the closure of the set X is the set X together with its limit points.
An operator that assigns a set to its closure is called a closure operator. I will refer to it as ⊛. Usually in mathematics it is not so designated, but we after all have the right to the designations.
It has several properties:
1) ⊛∅ = ∅
This means that the closure of the empty set is empty.
2) X⊆⊛X
The set is contained in its closure.
3) ⊛X = ⊛⊛X
The closure of the closure of the set is equal to the closure of the set
4) ⊛X∪⊛X '= ⊛ (X∪X')
The union of the closures is equal to the closure of the union.
These rules are called the Kuratovsky closure axioms.
I think one of the best ways to understand topology is to look at some very small topological space. For example, one that consists of only a few elements.

Suppose we have a set {a, b, c, d, e} equipped with the topology described in the figure. Consider a subset of this set {a, b, c}. What points are limiting for him in this topology? By definition, these will be those points that have points from {a, b, c} in each of their neighborhoods besides themselves. I showed the open neighborhood schematically with the help of circles. Points inside one circle are in one neighborhood (or in one open subset of a set). Therefore, we check for each point whether it has a neighborhood in which there are no points from {a, b, c}. Point a has such a neighborhood. This is a neighborhood where there is only a point a. So it is not a limiting point. In all neighborhoods of b there are points from {a, b, c} (besides b itself). Similarly for d and e. Etc. thus, from this scheme, we see that b, d, e are limit points for {a, b, c}, but a and c are not.
We equip the same spaces with an anti-discrete topology and see what happens.

In the anti-discrete topology, each point will be the limit for the set {a, b, c} (and for any other, except the set itself and the empty set). It is not for nothing that this topology is called the topology of stuck points, in it all points of space are stuck together with each other, you can't figure out exactly where. I would not want to live in a universe with an anti-discrete topology.
In discrete topology, we have the opposite situation. I tried to draw, but to be honest, I refused this idea. You do remember how many open sets there will turn out even in a relatively small set.
Looking at all these pictures, I want to define the concept of the interior of a set and a border. For example, when I was drawing sets outlined by a black outline, I immediately wanted to call this line the border of a set. However, so far we have not had the concept of boundaries and insides. And now it will be.
A point is called an interior point of a set when the set is its neighborhood. The interior of a set is the collection of all its interior points. In other words, the interior of a set is the largest open set contained in it. Those. the set is open only when it coincides with its interior. Agree, this is very similar to the closure definition.
The interior of any subset of the anti-discrete space is empty. In a discrete space, any subset coincides with its interior and with its closure at the same time.
The boundary of a set X (X subset of A) is the set of those points of A whose neighborhood contains both points X and A / X.
I drew such a picture, a little in the style of abstract artists came out.

Here you go. on this note, I end the article. For the exercise, you can think about which points are the boundary of the set {a, b, c} from the image, which are its interior (if any), which is its closure. And, of course, is it possible to disconnect the figures from the initial picture. And how to do it (very much develops spatial thinking). I promise to attach the answer to the last question to the following articles.
All for now.
Source: https://habr.com/ru/post/196488/
All Articles