In search of cryptographic GPSN

Hi% username%!

In today's post we will talk about the cryptographic strength of pseudo-random number generators (PRNG).
To begin with, let's define what crypto-resistant PRNG is (CGPSN).

KSGPSCH must satisfy the "test for the next bit." The meaning of the test is as follows: there should not be a polynomial algorithm that, knowing the first k bits of a random sequence, can predict k + 1 bits with a probability of more than 50%.

Wikipedia

Perhaps some of the readers used GPSN such as linear feedback shift registers (RLOS) or Mersenne's Whirlwind beloved by many programmers. I will try to show that both of these methods, despite the very good statistical properties and large periods, do not meet the above definition and cannot be considered cryptographically stable, and also offer, as an alternative, two very reliable PRNGs.

')

Shift register with linear feedback

Often it was possible to see how this method was proposed to be used for cryptographic purposes, therefore, with it, in fact, we begin. Generators of this kind consist of a shift register and feedback function.


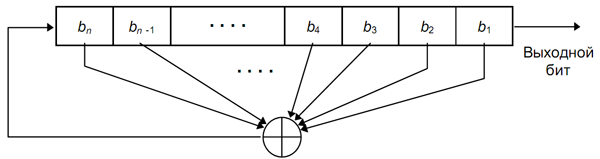
Each PRNG on RLOS is associated with a specific polynomial, which characterizes the register length and the feedback function. For example, a polynomial 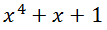matches the following register:


The degree of the polynomial determines the length of the register, non-zero members describe which elements of the register constitute a diversion sequence.
If the polynomial forming the diversion sequence is irreducible modulo 2, then the period generated by the register sequence will be maximum and calculated by the formula .

Before starting work, an arbitrary sequence of bits is entered into the register, which is called the initial state. After that, each clock cycle returns 1 bit, which looks completely random.
By themselves, RSLOS are good PRNGs, but due to the fact that the bits obtained with their help have a linear relationship, it is unwise to use RSLOS for cryptographic purposes.
If an attacker receives a sequence of bits of length n generated by the LFSR, he can load these bits into the register and scroll back to get the initial state. Knowledge of the initial state will give it access to all sequences generated earlier and generated in the future.

Hiding case information may seem like a good idea. Then, even having received a sequence of length n, the attacker cannot take steps to open the initial state.
But this situation is easily solved using the Berlekamp – Massey algorithm. This algorithm allows to reveal a polynomial associated with RSLOS. To do this, it is sufficient to have a register-generated sequence of only 2n length.
The algorithm is quite simple to implement:

public int[] BerlekampMassey(int[] array) { int N = array.Length; int[] b = new int[N]; int[] c = new int[N]; int[] t = new int[N]; b[0] = 1; c[0] = 1; int l = 0; int m = -1; for (int n = 0; n < N; n++) { int d = 0; for (int i = 0; i <= l; i++) { d ^= c[i] * array[n - i]; } if (d == 1) { Array.Copy(c, 0, t, 0, N); int N_M = (nm); for (int j = 0; j < N - N_M; j++) { c[N_M + j] ^= b[j]; } if (l <= n / 2) { l = n + 1 - l; m = n; Array.Copy(t, 0, b, 0, N); } } } return c; } 

The input is a sequence of bits generated using the LFSR. As a result, a polynomial characterizing the feedback scheme is returned.

Of course, the LFSR can be cascaded for a more robust PRNG. This idea is used in some stream ciphers. However, many generators based on this method are vulnerable to so-called correlation attacks. I gave some details about this type of attack in my recent post GSM Security: Data Encryption . Here I will only say that with the help of a correlation attack, an attacker, possessing a sequence of generated PRNG, has the ability to restore the initial value and gain access to all values ​​generated in the future.

Whirlwind of mersenne

In my opinion, the PRNG called the Mersenne Whirlwind is much more interesting. There are several variants of the algorithm. We consider only the most frequently used MT19937. We briefly describe this algorithm.
Mersenn's whirlwind consists of two parts: RSLOS and quenching.

The shift register consists of 624 elements, each 32 bits long. Initialization of the initial state is described by the function:

  function initialize_generator(int seed) { index := 0 MT[0] := seed for i from 1 to 623 { // loop over each other element MT[i] := last 32 bits of(1812433253 * (MT[i-1] xor (right shift by 30 bits(MT[i-1]))) + i) // 0x6c078965 } } 

A certain seed value is supplied to the input of the initialization function, with which the entire register is filled.

At the first and each subsequent 624th step, the internal state of the register is mixed:

  function generate_numbers() { for i from 0 to 623 { int y := (MT[i] & 0x80000000) // bit 31 (32nd bit) of MT[i] + (MT[(i+1) mod 624] & 0x7fffffff) // bits 0-30 (first 31 bits) of MT[...] MT[i] := MT[(i + 397) mod 624] xor (right shift by 1 bit(y)) if (y mod 2) != 0 { // y is odd MT[i] := MT[i] xor (2567483615) // 0x9908b0df } } } 

At each step, the algorithm returns the following number from the current state of the register and produces the so-called "hardening":

  function extract_number() { if index == 0 { generate_numbers() } int y := MT[index] // y := y xor (right shift by 11 bits(y)) y := y xor (left shift by 7 bits(y) and (2636928640)) // 0x9d2c5680 y := y xor (left shift by 15 bits(y) and (4022730752)) // 0xefc60000 y := y xor (right shift by 18 bits(y)) index := (index + 1) mod 624 return y } 

In order to gain access to the internal state of the algorithm, it is enough for an attacker to get a sequence consisting of 624 numbers.
All you need to do is to return the numbers generated by the algorithm to the state in which they were before the “quenching” stage. For this it is necessary to do all the steps of hardening in the opposite direction. For example, consider the last hardening step:
y := y ^ (y >>> 18)
Let's see what happens with binary data when performing this operation:
y 101101110101111001 11111001110010
y >>> 18 000000000000000010110111010111 100111111001110010
y ^ (y >>> 18) 101101110101111001 01001110100101
As you can see, the first 18 bits of the result and the original number are the same. In order to recover the remaining 14 bits, we need to do the following:
result ^ (result >>> 18)
Acting in a similar way for all steps of the quenching stage, we obtain the element of the initial state of the PRNG:

  private uint reverse(uint output) { uint tempout = output >> 18; output = output ^ tempout; tempout = output << 15; output = (uint)(output ^ (tempout & 4022730752)); uint a = output << 7; uint b = (uint)(output ^ (a & 2636928640)); uint c = b << 7; uint d = (uint)(output ^ (c & 2636928640)); uint e = d << 7; uint f = (uint)(output ^ (e & 2636928640)); uint g = f << 7; uint h = (uint)(output ^ (g & 2636928640)); uint i = h << 7; uint tempfinal = (uint)(output ^ (i & 2636928640)); uint k = tempfinal >> 11; uint l = (uint)(tempfinal ^ k); uint m = (uint)l >> 11; uint final = (uint)(tempfinal ^ m); return final;  } 

As I noted above, if an attacker has 624 numbers generated using the Mersenne Vortex, this is enough to restore the entire internal state and to predict with 100% probability all generated in the subsequent numbers.

Crypt resistant GPCH

As an alternative, I want to offer two very reliable methods.

Blum - Blum - Shub Algorithm
This generator is based on the complexity of solving the problem of factoring large numbers.
The algorithm generates a sequence of pseudo-random bits and consists of the following steps:

• Generate two large primes p, q, such that p = q = 3 mod 4.
• Calculate M = p * q.
• Take a large number x ₀ , mutually simple with M.
• At each step of generating the sequence, the number x _{i + 1} = x _i ² mod M is calculated.
• As a result, the last bit of the number x _{i is} returned.

To date, this algorithm is perhaps the most reliable PRNG. To open the initial state or guess the next element of a pseudo-random sequence, the attacker must know the numbers p and q.
The BBS generator has only one drawback - this is extremely low speed. To increase performance at each generation step, you can return instead of one, log (log M) bits. This will increase the speed without reducing the robustness.

CTR encryption mode
A faster, but equally reliable way to get a pseudo-random sequence is the CTR mode of encrypting block ciphers, in other words, the counter mode. As a encryption function, you can use any strong block cipher, for example AES.

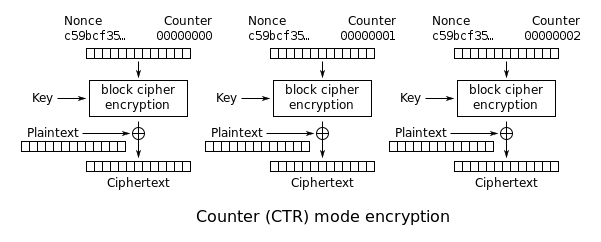
The encryption key and a 128-bit data block consisting of a random bit string and a counter are input to the encryption function. At each step, the counter is incremented by one, thus guaranteeing a non-repeating sequence of blocks. The generated sequence consists of encrypted blocks. In order to predict the next element of the generated sequence, the attacker needs to open the encryption key, i.e. the task is reduced to cracking of the block cipher used in the scheme.

Conclusion

First of all, I wanted to demonstrate the cryptographic unreliability of such well-proven PRNGs, such as linear feedback registers and the Mersenne Vortex.
Both of these algorithms are distinguished by high speed. They generate really good sequences that are statistically indistinguishable from random ones. But, unfortunately, when it comes to cryptography, this is often not enough and you need to use slower, but much more secure methods.