The number of false positive positives of the Bloom filter [translation]

The number of false positive positives of the Bloom filter.

Description

The Bloom Filter is a randomized query data structure developed by Burton Bloom in the 1970s. Bloom filter gives an erroneous answer to the request, the so-called. false positive response. Those. if we add some element, then there is a nonzero probability that the Bloom filter will return the answer that the element is in a vector, although it is not there.

Roughly speaking, the Bloom filter returns 2 possible answers:

1. no item in vector
2. element may be in vector

Bloom analyzed the probability of such erroneous answers, but his analysis is incorrect.

In the article I will not describe the construction of the Bloom filter, you can read about it in the corresponding article Bloom filter or on the WIKI wiki : Bloom filter
')

Introduction

The Bloom filter is a data structure that maps a set of S of n elements into a bit vector. . To record an element, k -chase hash functions are used, such that . Initially, the vector is initialized with zeros. The element is written by setting all k- bits in the unit to vector B, i.e. 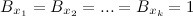. To check the existence of an item in the filter it is enough to know the values ​​of each k- bit of the vector. If there is at least one zero, it means that there is no such element in the vector yet, and if all the bits are set to one, this indicates that the element probably already exists. This situation is called a false positive response.

Bloom counted false positives as follows:
The probability that any bit of B is zero is after installing all units of k- hash functions when adding n- elements.
Therefore, the probability that a particular bit will be set to one is

Now that would lead 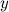to false positive positives, each of the k -bits of the vector must be set to one. The probability of this: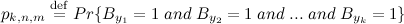

which is claimed to be equal

This is a proof that appeared many years ago incorrect. The error lies in the fact that an implicit assumption is made that the event and event 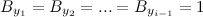considered independent. At first glance, this seems to be true, since are independent. However, a simple counterexample to the proof can be obtained considering the case 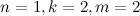. In this case, a simple listing of 16 possible situations reveals the probability of a false positive response as 5/8 , while the Bloom formula gives the result 9/16 = 4.5 / 8

Exact formula

Let us model the problem of determining the number of false-positive positives as the problem of balls and baskets. We have m- cart. We throw a kn of white balls into random baskets. We can consider a basket as white if it contains at least one white ball. Next we place k -black balls in the baskets. Let event A be that each black ball is located in a white basket. Calculate the probability of this event. .
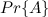Note that the set of white baskets can be represented as a subset 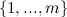. For anyone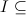 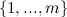denote 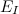as an event that I is a set of white baskets. Power I is equal to 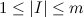. We use the conditional probability formula: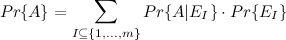

If I is fixed, then

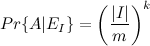
where contains

• the number of mappings from the set of the size of kn to the set of values ​​of i and
• the number of functions from a set of size kn to a set of size m

The number of mappings from the set of size kn to the set of size i is described by the formula 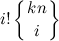where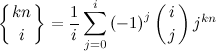


The number of functions from a set of size kn to a set of size m is .

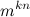Combine these formulas:

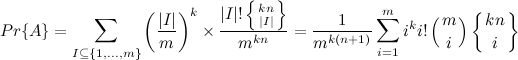
Final result

As a result, it turns out that the probability of false positive positives of the Bloom filter from m bits when adding n elements using k- hash functions is equal to:


This formula is no longer as simple as Bloom originally calculated. Without going into further details, I will say that the authors of the article also describe the upper and lower bounds of this formula and come to the conclusion that the initial formula that Bloom derived can only be used as a lower bound.



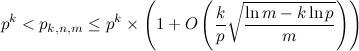
Original article text:
ON THE FALSE-POSITIVE RATE OF BLOOM FILTERS