Lock-free data structures. Basics: Atomicity and atomic primitives

The construction of a lock-free data structure is based on two pillars — atomic operations and ways to streamline memory access. This article focuses on atomicity and atomic primitives.

Announcement . Thank you for the warm welcome. Beginning ! I see that the lock-free theme is interesting for the habrasoobschestvu, it makes me happy. I planned to build a cycle according to the academic principle, smoothly moving from fundamentals to algorithms, simultaneously illustrating the text with the code from libcds. But some readers require spectacles without delay to show how to use the library, especially not rassusolivaya. I agree, there is a reason for this. Ultimately, and I'm not so interested in what's inside the boost , - describe how to use it! Therefore, I will divide my epic cycle into three parts: Basics , Inside and Outside . Each article of the epic will be related to one of the parts. The Basics will talk about low-level things, up to the structure of modern processors; This is the part for how many people like me. Inside it will highlight interesting algorithms and approaches in the world of lock-free, it’s rather a theory about how to implement a lock-free data structure, libcds will be an inexhaustible source of C ++ code. In Outside there will be articles on the practice of using libcds, - software solutions, tips and FAQ. From the outside will eat your questions / comments / suggestions, dear habrazhiteli.

In the meantime, I frantically prepare the beginning of the Outside - the first part of the Basics . The article is largely not about C ++ (although about it too) and not even about lock-free (although algorithms are not functional without atomic lock-free), but about the implementation of atomic primitives in modern processors and the basic problems encountered when using such primitives.
Atomicity is the first circle of hell, a low level of two.

Atomic operations are divided into simple - read and write - and atomic change operations (read-modify-write, RMW). An atomic operation can be defined as an indivisible operation: it has either already taken place or not yet; we can not see any intermediate stages of its implementation, no partial effects. In this sense, even simple read / write operations, in principle, can be non-atomic; for example, reading unaligned data is non-atomic: in the x86 architecture, such reading will result in an internal exception that causes the processor to read the data in parts, in other architectures (Sparc, Intel Itanium) - in a fatal error (segmentation fault), which, in principle, can be intercepted and process, but about the atomicity of speech here can not be. In modern processors, atomicity of reading / writing of only aligned simple (integral) types - integers and pointers is guaranteed. A modern compiler ensures correct alignment of variables of base types, although it is not difficult to write an example of unaligned conversion, for example, to the whole. If you want to work atomically with a structure (4-4 byte size), then you should take care of proper alignment using compiler directives (attributes) (each compiler supports its own unique way of specifying data / type alignment). By the way, the library libcds contains a set of auxiliary types and macros that hide the compiler-dependent part when declaring aligned data.
')

Compare-and-swap

It is rather difficult, if at all possible, to invent an algorithm for a lock-free container using only read / write (I don’t know such data structures for an arbitrary number of threads). Therefore, the developers of processor architectures have implemented RMW operations that can atomically read a aligned memory cell and write to it: compare-and-swap (CAS), fetch-and-add (FAA), test-and-set (TAS), etc. In the academic environment, the compare-and-swap operation (CAS) is considered as the base operation; her pseudocode is simple:

bool CAS( int * pAddr, int nExpected, int nNew ) atomically { if ( *pAddr == nExpected ) { *pAddr = nNew ; return true ; } else return false ; } 

In words: if the current value of the variable at the address pAddr is equal to the expected nExpected , then assign the variable the value nNew and return true , otherwise return false , the value of the variable does not change. All this is done atomically, that is, indivisibly and without visible partial effects. Through CAS, you can express all other RMW operations, for example, fetch-and-add will look like this:

 int FAA( int * pAddr, int nIncr ) { int ncur ; do { ncur = *pAddr ; } while ( !CAS( pAddr, ncur, ncur + nIncr ) ; return ncur ; } 

The “academic” version of the CAS operation is not always convenient in practice, because often when CAS fails, we wonder what the value is in the cell now. Therefore, such a CAS variant is often considered (the so-called valued CAS , also performed atomically):

 int CAS( int * pAddr, int nExpected, int nNew ) atomically { if ( *pAddr == nExpected ) { *pAddr = nNew ; return nExpected ; } else return *pAddr } 

In C ++ 11, the compare_exchange function (strictly speaking, in C ++ 11 there is no such function, there are its variants compare_exchange_strong and compare_exchange_weak , but I will tell about them later) covers both of these options:

 bool compare_exchange( int volatile * pAddr, int& nExpected, int nNew ); 

The nExpected argument nExpected passed by reference, and the input contains the expected value of the variable at pAddr , and the output is the value before the change. Returns the function success sign: true if the address is nExpected (in this case it changes to nNew ), false if it fails (then nExpected will contain the current value of the variable at pAddr ). Such a universal construction of the CAS operation covers both variants of the “academic” definition of CAS, but in practice the application of compare_exchange fraught with errors, since it must be remembered that the nExpected argument nExpected passed by reference and can be changed, which is not always acceptable.
Using compare_exchange fetch-and-add primitive shown above can be written like this:

 int FAA( int * pAddr, int nIncr ) { int ncur = *pAddr; do {} while ( !compare_exchange( pAddr, ncur, ncur + nIncr ) ; return ncur ; } 

ABA problem

Primitive CAS is good for everyone, but its application can cause a serious problem, called the ABA-problem . To describe it, consider the typical pattern of using the CAS operation:

 int nCur = *pAddr ; while (true) { int nNew =    if ( compare_exchange( pAddr, nCur, nNew )) break; } 

In fact, we are “dug” in the cycle until the CAS works; the cycle is necessary because between reading the current value of a variable at pAddr and calculating the new value of nNew variable at address pAddr can be changed by another thread.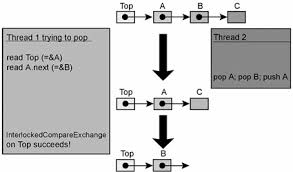


The ABA problem is described as follows: for example, a stream X reads the value A from some shared cell containing a pointer to some data. Then another thread, Y, changes the value of this cell to B and again to A, but now the pointer A points to other data. When flow X using the CAS primitive tries to change the cell value, the pointer is compared with the previous (read) value of A successfully, and the CAS result is successful, but A now points to completely different data! As a result, the flow can break the internal connections of the object (which, in turn, can lead to a crash).

Here is the implementation of a lock-free stack subject to the ABA problem [Mic04]:

 // Shared variables static NodeType * Top = NULL; // Initially null Push(NodeType * node) { do { /*Push1*/ NodeType * t = Top; /*Push2*/ node->Next = t; /*Push3*/ } while ( !CAS(&Top,t,node) ); } NodeType * Pop() { Node * next ; do { /*Pop1*/ NodeType * t = Top; /*Pop2*/ if ( t == null ) /*Pop3*/ return null; /*Pop4*/ next = t->Next; /*Pop5*/ } while ( !CAS(&Top,t,next) ); /*Pop6*/ return t; } 

The following sequence of actions leads to a violation of the stack structure (note that this sequence is not the only one illustrating the ABA problem):

Thread x	Thread y
Causes Pop() . Pop4 string Pop4 , variable values: t == A next == A->next
	NodeType * pTop = Pop() pTop == top of stack, i.e. A Pop() Push( pTop ) Now top of the stack - again a Note that A->next has changed.
The string Pop5 is Pop5 . CAS is successful, but the field Top->next is assigned a value nonexistent in the stack since stream y pushed out from stack A and A->next , and local variable next stores the old value of A->next

The ABA problem is the scourge of all lock-free containers based on the CAS primitive. It can occur only in a multi-threaded code due to the removal of element A from the container and replacing it with another (B), and then again with A (hence the name “ ABA Problem”), while another thread holds a pointer to the element to be deleted. Even if the thread physically deletes A ( delete A ) and then calls new to create a new element, there is no guarantee that the allocator will not return Address A (good allocators will do just that). Often it manifests itself in a more sophisticated way than described above, it affects not two, but more streams (in this sense we can talk about the ABCBA problem, the ABABA problem, etc., how much fantasy is enough), and its identification is always a non-trivial task. . The ABA problem control tool is deferred physical removal ( deferred deallocation , or safe memory reclamation ) of an element at the moment when there is a complete guarantee that no one (none of the competing streams) has any local or global references to the element to be deleted.
Thus, deleting an element from the lock-free structure is two-phase:

• The first phase is the exclusion of an element from the lock-free container;
• The second phase (deferred) - the physical removal of the element when there is no reference to it.

I will discuss in detail the various pending removal schemes in one of the following articles.

Load-Linked / Store-Conditional

Probably, the presence of an ABA-problem when using CAS prompted the processor designers to search for other RMW-operations that are not subject to the ABA-problem. And such operations were found - a pair of load-linked / store-conditional (LL / SC). These operations are very simple - here is their pseudocode:

 word LL( word * pAddr ) { return *pAddr ; } bool SC( word * pAddr, word New ) { if (   pAddr      LL) { *pAddr = New ; return true ; } else return false ; } 

A pair of LL / SC works as operator brackets. The load-linked (LL) operation simply returns the current value of the variable to the address pAddr . The store conditional (SC) operation saves to the address previously read by the LL operation pAddr only if the data in pAddr not changed since it was read. In this case, a change is any modification of the cache line to which the address pAddr . To implement the LL / SC pair, the processor developers had to change the cache structure: roughly speaking, each cache line must have an extra status bit. When reading by the LL operation, this bit is set (link), during any write to the cache line (or it is preempted from the cache), the bit is cleared, and the SC operation checks before storing whether the bit is set to the cache line: if the bit = 1, then there is no one changed the cache line, the value at the address pAddr changes to a new one and the operation SC is successful, otherwise the operation fails, the value at the address pAddr does not change.

The CAS primitive can be implemented using the LL / SC pair like this:

 bool CAS( word * pAddr, word nExpected, word nNew ) { if ( LL( pAddr ) == nExpected ) return SC( pAddr, nNew ) ; return false ; } 

Note that, despite the multistepness of this code, it executes an atomic CAS: the contents of the target memory cell either do not change or change atomically . The implementation of the LL / SC pair on architectures that support only the CAS primitive is possible, but not so primitive; I will not consider it here, referring to those interested in the article [Mic04].

Modern processor architectures are divided into two large camps - some support the CAS primitive in their command system, while others support the LL / SC pair. CAS is implemented in x86, Intel Itanium, Sparc; the primitive first appeared in the IBM System 370 architecture. The LL / SC pair is PowerPC, MIPS, Alpha, ARM; first proposed by the DEC. It is worth noting that the LL / SC primitive is implemented in modern architectures not in the most ideal way: for example, you cannot make nested LL / SC calls with different addresses, false flag resets are possible (so called false sharing, see below), there is no flag validation primitive linked inside a pair of LL / SC.

From the point of view of C ++, the C ++ 11 standard does not consider a pair of LL / SC, but describes only the atomic primitive compare_exchange (CAS) and atomic primitives derived from it - fetch_add , fetch_sub , exchange , etc. The standard implies that you implement CAS using LL / SC is quite simple, but the reverse implementation - LL / SC via CAS - is very nontrivial. Therefore, in order not to complicate the lives of the developers of the standard C ++ library, the standardization committee has introduced only compare_exchange in C ++, which, in principle, is sufficient to implement lock-free algorithms.

False sharing

In modern processors, the cache line length L (cache line) is 64 - 128 bytes and tends to increase in new models. Data is exchanged between the main memory and the cache in L byte blocks (usually L is a power of 2). When changing at least one byte in the cache line, the entire line is considered invalid and requires synchronization with the main memory. This is governed by the cache coherence support protocol in the multiprocessor / multi-core architecture.


If different shared data falls into one cache line (that is, located in adjacent addresses), then changing one data leads, from the point of view of the processor, to the invalidation of others that are on the same cache line. This situation is called false sharing . For LL / SC primitives, false sharing is destructive, since the implementation of these primitives is performed in terms of cache lines: the Load-Linked operation marks (link) the cache line, and the Store-Conditional operation checks whether the link flag is not reset for this line ; if the flag is cleared, no entry is performed and the SC returns false. Since the length of the L line is quite large, the false non- triggering of the SC primitive (that is, the reset of the link flag) happens with any change in the cache line that is not associated with the target data. As a result, we can get livelock : a situation where the processors / cores are 100% occupied, but there is no progress.

The fight against false sharing is fairly simple (but wasteful): each shared variable must occupy the entire cache line; for this, padding is usually used:

 struct Foo { int volatile nShared1; char _padding1[64]; // padding for cache line=64 byte int volatile nShared2; char _padding2[64]; // padding for cache line=64 byte }; 

It should be noted that the physical structure of the cache affects all operations (including CAS), and not just the LL / SC primitives. In some papers, data structures that are specially constructed taking into account the cache structure (mainly taking into account the length of the cache line) are investigated; with proper (“under the cache”) data structure, performance can increase by an order of magnitude.

CAS Varieties

I will briefly dwell on two more useful atomic primitives - double-width CAS (double-word CAS, dwCAS) and double CAS (DCAS).

Double-width CAS is similar to the usual CAS, but it operates with a double-sized memory cell: 64-bit for 32-bit architectures and 128-bit (more precisely, at least 96-bit) for 64-bit. For architectures that provide a pair of LL / SC instead of CAS, LL / SC should also operate with words of double length. Of all the architectures I know, only x86 supports dwCAS. Why is this primitive so useful? It allows you to organize one of the first schemes for solving ABA-problems - tagged pointers . This scheme was proposed by IBM just to solve an ABA-problem and consists in comparing each divided pointer tag - an integer number; The tagged pointer can be described by the following structure:

 template <typename T> struct tagged_pointer { T * ptr ; uintptr_t tag ; tagged_pointer() : ptr( new T ) , tag( 1 ) {} }; 

To ensure atomicity, this type must be double-aligned: 8 bytes for 32-bit architectures and 16 bytes for 64-bit architectures. The tag contains the “version number” of the data pointed to by ptr . I will talk in detail about tagged pointers in one of the following articles on safe memory management (safe memory reclamation, SMR), but here I’ll just note the fact that tagged pointers implies that the memory once allocated for data of type T (and the corresponding tagged_pointer ) should not be physically deleted ( delete ), but should be placed in the free-list (separate for each type T), from which further data will be re-distributed with the increment of the tag. This is exactly what the ABA problem gives a solution: in fact, our pointer is composite and contains the version number in the tag (the ordinal number of the distribution); in this case, dwCAS will not succeed if in its arguments of the tagged_pointer type tagged_pointer pointers are equal and the tag values ​​are different.

The second atomic primitive - dual CAS (DCAS) - is currently purely hypothetical and is not implemented in any of the modern processor architectures. The pseudocode of DCAS is:

 bool DCAS( int * pAddr1, int nExpected1, int nNew1, int * pAddr2, int nExpected2, int nNew2 ) atomically { if ( *pAddr1 == nExpected1 && *pAddr2 == nExpected2 ) { *pAddr1 = nNew1 ; *pAddr2 = nNew2 ; return true ; } else return false } 

DCAS operates on two arbitrary aligned memory cells and changes the values ​​in both if the current values ​​coincide with the expected ones.

Why is this primitive so interesting? The fact is that with its help it is quite easy to build a lock-free doubly linked list (deque, double-linked list), and such a data structure is the basis of many interesting algorithms. There are a large number of academic papers dedicated to DCAS-based data structures. Although this primitive is not implemented “in hardware”, there are works (for example, [Fra03] is the most famous of them) describing the DCAS generation algorithm (and multi-CAS in general for any number of addresses pAddr1 ... pAddrN ) based on the usual CAS.

Performance

And what about the performance of atomic primitives?
Modern processors are so complex and unpredictable that manufacturers do not give any unequivocal guarantees of the duration of certain instructions, especially atomic ones, which involve internal synchronization, signaling of processor buses, etc. There are quite a large number of works in which the authors try measure the duration of the processor instructions. I will give the measurements from [McKen05]. In this paper, the authors, among other things, compare the duration of the atomic increment and the CAS primitive with the duration of the operation nop (no-operation). So, for Intel Xeon 3.06 GHz (sample of 2005), the atomic increment has a duration of 400 nop, CAS - 850 - 1000 nop. IBM Power4 1.45 GHz processor: 180 nop for atomic increment and 250 nop for CAS. The measurements are quite old (2005). Since then, the processor architecture has taken a few more steps forward, but the order of numbers, I think, has remained the same.

As you can see, atomic primitives are pretty heavy. Therefore, it is quite expensive to apply them everywhere: for example, if a binary tree search algorithm uses CAS to read the current tree node, I do not expect anything good from such an algorithm (I have seen such algorithms). In fairness it should be noted that, according to my feelings, with each new generation of the Intel Core architecture, the CAS primitive is becoming faster, apparently, Intel engineers put a lot of effort into improving the micro-architecture.

Volatile and atomicity

C ++ has a mysterious volatile keyword. Sometimes volatile associated with atomicity and ordering - this is wrong, but has some historical basis.
In fact, volatile guarantees only that the compiler will not cache the value in the register (optimizing compilers love to do this: the more registers - the more caches). That is, reading a volatile variable always means reading from memory, writing a volatile variable is always writing to memory. Therefore, if someone simultaneously changes volatile data, we will immediately see it.
In fact, we will not see. Because of the lack of memory barriers. In some languages ​​(Java, C #), volatile assigned a magic status that provides ordering, but not in C ++ 11. And no special alignment of volatile does not guarantee, and we now know that a necessary condition for atomicity is just the correct alignment of data.
Thus, for a C ++ 11-compatible compiler, the indication volatile for an atomic variable is redundant. But for the old compiler it is necessary if you implement atomic yourself. In this ad:

 class atomic_int { int m_nAtomic; //…. }; 

the compiler has the full right to “optimize” the calls to m_nAtomic (despite the fact that the call goes indirectly through this ). Therefore, it is int volatile m_nAtomic to specify int volatile m_nAtomic .

libcds

In conclusion, what do we have in the libcds library ? And we have another bike implementation of atomic primitives in the spirit of C ++ 11 for x86 / amd64, Intel Itanium and Sparc architectures. If the compiler does not support C ++ 11 (and only the newest versions of compilers support it - GCC 4.7+, MS Visual C ++ 2012, Clang 3.0+ available to me), then libcdsuse its implementation of atomic primitives. In this case, the main atomic primitive for constructing lock-free data structures, in addition to the usual atomic read / write, is CAS, very rarely where CAS is used over a double word (dwCAS). DCAS implementations (and multi-CAS in general) inlibcds[not yet], but it is quite possible that it will appear in the future - very interesting data structures can be built on it. It stops only that, according to many studies, the implementation of DCAS using the [Fra03] algorithm is rather inefficient. But I already noted that the criterion of efficiency is a purely individual thing in the world of lock-free: what is ineffective now on this gland and for this task can be extremely effective then either on another gland or for another task!

In the next article on Basics, we’ll talk about ordering memory access (memory ordering) - about memory barriers (memory fence, memory barrier).

Links:

[Cha05] Dean Chandler Reduce False Sharing in .NET , 2005, Intel Corporation

[Fra03] Keir Fraser Practical Lock Freedom , 2004; technical report is based on a dissertation submitted September 2003 by K.Fraser for the degree of Doctor of Philosophy to the University of Cambridge, King's College

[McKen05] Paul McKenney, Thomas Hart, Jonathan Walpole Practical Concerns for Scalable Synchronization

[Mic04] Maged Michael ABA Prevention using single-word instruction , IBM Research Report, 2004