Binary heap: proof of the complexity of the construction of O (n)
Actually, it will be a question of the binary heap and its construction using Sift-Down (or Heapify). Many probably know that building a heap in this way is done in 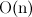 . Here I will give evidence of this fact.
. Here I will give evidence of this fact.
Here is an example of the procedure for constructing a heap by array in the Pascal language.
So, let an array consisting of elements, and
elements, and  number of operator calls
number of operator calls  (in the procedure
(in the procedure  ) when building a heap on this array. Obviously
) when building a heap on this array. Obviously  determines the time of the procedure
determines the time of the procedure  which is interesting to us.
which is interesting to us.
')
 was done
was done 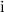 operator calls
operator calls  . Then his index did not exceed
. Then his index did not exceed  .
.
With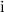 operator calls
operator calls  index
index  element increases at least in
element increases at least in 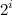 time. Now let
time. Now let 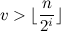 i.e.
i.e.  . Then after
. Then after 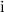 we have calls
we have calls  that is impossible, as in our heap
that is impossible, as in our heap  items.
items. 
Let us now estimate the magnitude above . Let an array element have an index
. Let an array element have an index  . There is
. There is 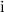 such that
such that  . Then in order for the array element with the index
. Then in order for the array element with the index  He took his place in the heap will need no more
He took his place in the heap will need no more 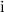 calls
calls  (by the lemma). The number of elements with such indices is the value
(by the lemma). The number of elements with such indices is the value 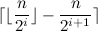 that when
that when 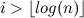 vanishes.
vanishes.
In this way,

With the terms are zero (so the loop in the procedure
the terms are zero (so the loop in the procedure  can start with
can start with 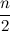 ).
).
We estimate the left multiplier in each term sum as

From here we have:
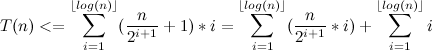
We estimate each of the amounts.
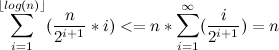
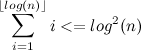
In this way,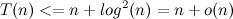 .
.
 bounded above by a function that is
bounded above by a function that is 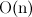 . So
. So 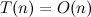 .
.
Consequently, the time of the procedure there is a proportional value
there is a proportional value 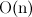 .
.
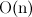 . Here I will give evidence of this fact.
. Here I will give evidence of this fact.Here is an example of the procedure for constructing a heap by array in the Pascal language.
procedure siftdown(v:longint); var min,l,r:longint; begin l:=v*2; r:=v*2+1; min:=v; if (l <= s) and (a[l] < a[min]) then min:=l; if (r <= s) and (a[r] < a[min]) then min:=r; if min <> v then begin swap(a[min], a[v]); sift_down(min); end; end; procedure build; var i:longint; begin for i:=n downto 1 do siftdown(i); end; So, let an array consisting of
 elements, and
elements, and  number of operator calls
number of operator calls 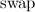 (in the procedure
(in the procedure 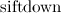 ) when building a heap on this array. Obviously
) when building a heap on this array. Obviously  determines the time of the procedure
determines the time of the procedure  which is interesting to us.
which is interesting to us.')
Lemma.
Let for some element of the array when calling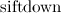 was done
was done 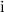 operator calls
operator calls 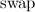 . Then his index did not exceed
. Then his index did not exceed  .
.Evidence:
With
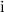 operator calls
operator calls 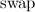 index
index  element increases at least in
element increases at least in 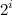 time. Now let
time. Now let 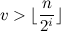 i.e.
i.e.  . Then after
. Then after 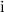 we have calls
we have calls  that is impossible, as in our heap
that is impossible, as in our heap  items.
items. 
Let us now estimate the magnitude above
 . Let an array element have an index
. Let an array element have an index  . There is
. There is 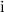 such that
such that  . Then in order for the array element with the index
. Then in order for the array element with the index  He took his place in the heap will need no more
He took his place in the heap will need no more 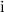 calls
calls  (by the lemma). The number of elements with such indices is the value
(by the lemma). The number of elements with such indices is the value 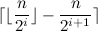 that when
that when 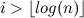 vanishes.
vanishes.In this way,

With
 the terms are zero (so the loop in the procedure
the terms are zero (so the loop in the procedure  can start with
can start with 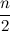 ).
).We estimate the left multiplier in each term sum as

From here we have:
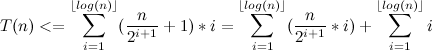
We estimate each of the amounts.
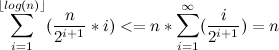
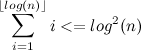
In this way,
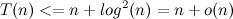 .
. bounded above by a function that is
bounded above by a function that is 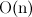 . So
. So 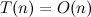 .
.Consequently, the time of the procedure
 there is a proportional value
there is a proportional value 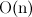 .
.Source: https://habr.com/ru/post/195832/
All Articles