Gravitational search. Gravitational search
Foreword
Good day to all. I present to you the following article from a series of coverage of new and little-known heuristic optimization methods. Today's post owes its appearance to Esmatu Rashedi, Isaac Newton and gravity.

History reference
Gravitational search (GS) is a very young algorithm. It appeared in 2009 and was a logical development of the central force method. The basis of GS are the laws of gravity and the interaction of the masses. In principle, this algorithm is similar to Particle Swarm Optimization (PSO) methods, since it is based on the development of a multi-agent system.
Strategy
GS operates with two laws:
- Each particle attracts others and the force of attraction between two particles is directly proportional to the product of their masses and inversely proportional to the distance between them (attention should be paid to the fact that, unlike the Universal Law of the World, not the square of the distance; Rashedi explains this by the fact that tests it gives the best results, leave it on his conscience)
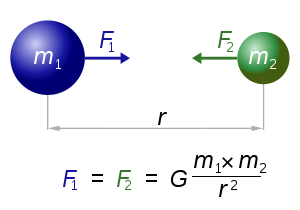
- motion: the current speed of any particle is equal to the sum of the part of the speed at the previous time and the change in speed, which is equal to the force with which the system acts on the particle divided by the inertial mass of the particle.
Having these two laws in the arsenal, the method works according to the following plan:
- random generation of the system
- determination of the fitness of each particle,
- update of the values of the gravitational constant, the best and worst particles, as well as the masses,
- counting the resultant force in different directions,
- counting accelerations and speeds
- particle position updates,
- repetitions of steps 2–6 before the completion criterion is met (or the maximum number of iterations is exceeded, or the position change is too small, or any other reasonable criterion is
pleasing to your soul).
For those who are interested in a more detailed description of the algorithm
So, we have some function that needs to be minimized:  . In addition, there is an area
. In addition, there is an area 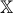 in which the initial positions of the particles are generated. In accordance with the GS work plan, everything begins with the generation of a particle system
in which the initial positions of the particles are generated. In accordance with the GS work plan, everything begins with the generation of a particle system  where
where  - The maximum number of particles in the system.
- The maximum number of particles in the system.
Force acting at time on
on  particle from the side
particle from the side 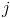 th, calculated by the formula
th, calculated by the formula 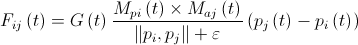 where
where 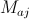 - active gravitational mass
- active gravitational mass 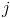 particles
particles  - passive gravitational mass
- passive gravitational mass 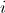 particles
particles 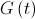 - gravitational constant at the appropriate time,
- gravitational constant at the appropriate time,  - small constant
- small constant 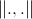 - Euclidean distance between particles.
- Euclidean distance between particles.
')
So that the algorithm was not deterministic, but stochastic, in the formula for calculating the resultant force random variables are added
random variables are added  (evenly distributed from zero to one). Then the resultant force is
(evenly distributed from zero to one). Then the resultant force is 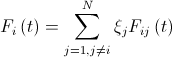 .
.
Calculate the acceleration and speed: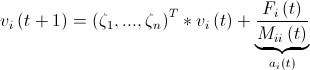 where
where  - operation of component multiplication of vectors,
- operation of component multiplication of vectors,  - random variable uniformly distributed from zero to one,
- random variable uniformly distributed from zero to one, 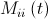 - inert mass
- inert mass  particles
particles
It remains to recalculate the position of the particles. This is very easy to do: .
.
By the current moment, two questions remain: how the gravitational constant changes and how to calculate the masses of the particles. The value of the gravitational constant should be determined by a monotonically decreasing function, depending on the initial values of the constant and time points
and time points  i.e.
i.e. 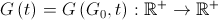 .
.
For example, you can take the following functions:
Now we can proceed to the final part of the story: to recalculate the masses. In the simplest case, all three masses (passive, active and inertial) are equal: . Then the value of the masses can be recalculated by the formula:
. Then the value of the masses can be recalculated by the formula: 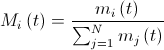 where
where 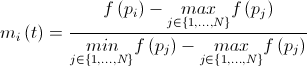 .
.
Of course, the masses can be calculated on the basis of their physical meaning; nevertheless, Rashedi does not speak about this (and none of the authors I could find).
 . In addition, there is an area
. In addition, there is an area 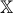 in which the initial positions of the particles are generated. In accordance with the GS work plan, everything begins with the generation of a particle system
in which the initial positions of the particles are generated. In accordance with the GS work plan, everything begins with the generation of a particle system 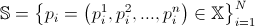 where
where  - The maximum number of particles in the system.
- The maximum number of particles in the system.Force acting at time
 on
on 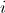 particle from the side
particle from the side 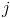 th, calculated by the formula
th, calculated by the formula 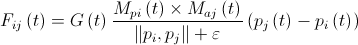 where
where 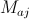 - active gravitational mass
- active gravitational mass 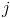 particles
particles  - passive gravitational mass
- passive gravitational mass 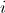 particles
particles 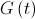 - gravitational constant at the appropriate time,
- gravitational constant at the appropriate time,  - small constant
- small constant 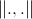 - Euclidean distance between particles.
- Euclidean distance between particles.')
So that the algorithm was not deterministic, but stochastic, in the formula for calculating the resultant force
 random variables are added
random variables are added  (evenly distributed from zero to one). Then the resultant force is
(evenly distributed from zero to one). Then the resultant force is 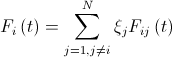 .
.Calculate the acceleration and speed:
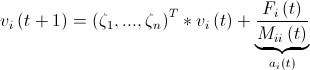 where
where  - operation of component multiplication of vectors,
- operation of component multiplication of vectors,  - random variable uniformly distributed from zero to one,
- random variable uniformly distributed from zero to one,  - inert mass
- inert mass  particles
particlesIt remains to recalculate the position of the particles. This is very easy to do:
 .
.By the current moment, two questions remain: how the gravitational constant changes and how to calculate the masses of the particles. The value of the gravitational constant should be determined by a monotonically decreasing function, depending on the initial values of the constant
 and time points
and time points  i.e.
i.e. 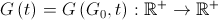 .
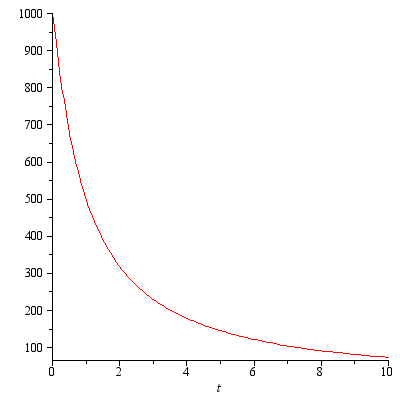
.For example, you can take the following functions:
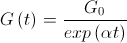 where
where 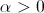 :
: 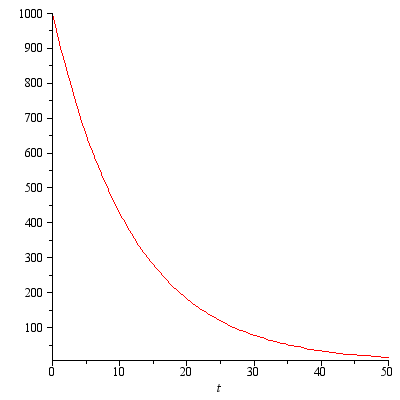 ,
, where
where  :
:  ,
,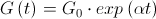 where
where  :
: 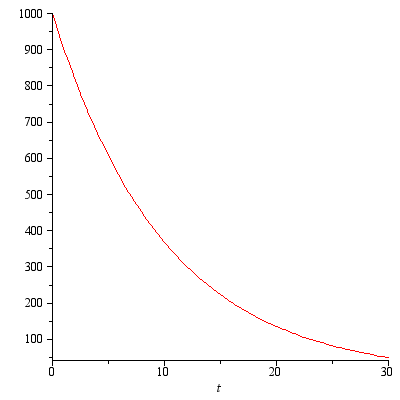 .
.
Now we can proceed to the final part of the story: to recalculate the masses. In the simplest case, all three masses (passive, active and inertial) are equal:
 . Then the value of the masses can be recalculated by the formula:
. Then the value of the masses can be recalculated by the formula: 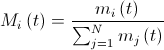 where
where 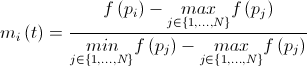 .
.Of course, the masses can be calculated on the basis of their physical meaning; nevertheless, Rashedi does not speak about this (and none of the authors I could find).
Pros and cons
pros
- as in the case of the harmonic search, the ease of implementation,
- in practice, the method is more accurate than genetic algorithms with real coding and classical PSO,
- greater convergence rate than genetic algorithms with real coding and classic PSO.
Minuses
- not the greatest speed due to the need to recalculate many parameters
- Most of the advantages are lost when optimizing multimodal functions (especially large dimensions), as the method begins to quickly converge to some local optimum, from which it is difficult to get out, since procedures are not provided that are similar to mutations in genetic algorithms.
Used sources
- The work of Rashedi himself (in case someone has access to their library),
- Excellent article by Karpenko, in which many algorithms are briefly described (I will refer to it more than once in the future),
- Selection of articles.
It can be useful
Afterword
On this, perhaps, familiarity with the method of gravitational search should be finished. I really hope that this post is better than the previous one. It remains only to vote on the topic of the next post.
Source: https://habr.com/ru/post/194674/
All Articles