Algorithm X or what is common between the wooden puzzle and the dancing Link?

Foreword
Once at a party a puzzle came into my hands, in which out of 25 identical figures it was required to assemble a cube. I was busy with her almost the whole evening, and as you can guess, absolutely to no avail. However, I could not give up just like that.
You can not do it yourself - force the computer. No sooner said than done. As a result, a whiming algorithm had to work all night to find all 4 unique solutions. In the process of google solutions for comparison, I found the program Burr Tools , which coped with this task in 3 minutes on my laptop.
')
Such a difference in speed made me figure out how this problem is being solved and a whole class of similar ones.

Puzzle description 25N puzzle cube
25 “voluminous” type N pentaminos are provided to you.
Each pentamine consists of five cubes.
From these figures it is required to make a cube of size 5 × 5 × 5.

25 “voluminous” type N pentaminos are provided to you.
Each pentamine consists of five cubes.
From these figures it is required to make a cube of size 5 × 5 × 5.
This puzzle is a classic representative of the exact coverage problem .
Mathematical wording
Suppose that we have given the set X, and the set of its subsets S. Then the task is to select from the set S, a subset S * such that every element of X is contained in exactly one element S *.
The formulation of the problem can be presented by the following example. You come to the store for collectible cards. What decks you should buy to build a complete collection without duplicate cards?
For such a task, there is Algorithm X of Donald Knuth . But before proceeding to the consideration of the algorithm, let's see how to reduce our puzzle with the creation of a cube to the problem of exact coverage.
Task formalization
For simplicity, we will solve a similar problem of folding from a four flat corners of a larger corner. If the figure is folded, then each square of the figure belongs to one and only one corner, which, you see, already sounds very similar to the formulation of the problem of complete coverage.
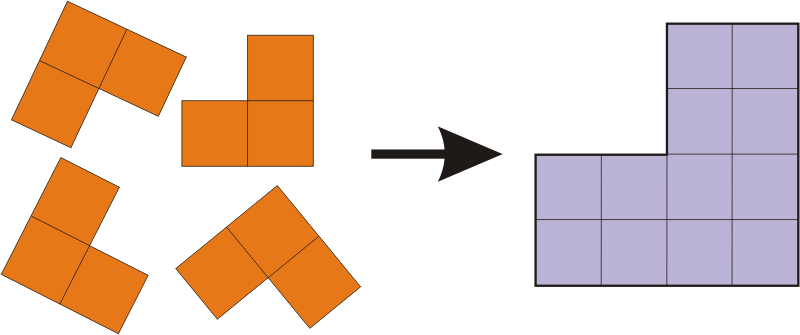
Let us denote by numbers all small squares of a large figure, and letters all possible positions of a small corner inside it (here, for the sake of clarity, some “bad” positions of the corners are deliberately thrown out, which precisely cannot be present in the solution). The combination of 12 squares is exactly what we will try to cover with the provisions of AL. The task can also be presented in the form of a table ( matrix of incidence ). The columns will correspond to the squares, the rows to the positions of the corner, and the unit at the intersection of the column and the line is placed if the corresponding position of the corner covers the corresponding box.
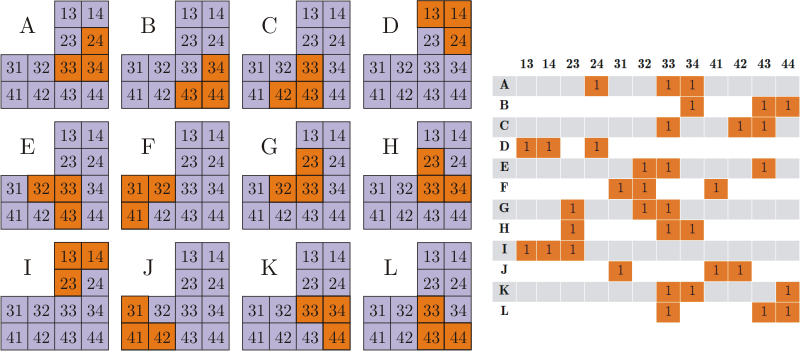
Task statement through matrix
Let us be given a matrix S consisting of zeros and ones. It is required to remove a certain number of rows from this matrix so that in the remaining matrix each column contains exactly one unit.
Slightly less obvious are the problem of complete coverage of a puzzle in which all the pieces are different, or a game like sudoku. The reader is invited to independently figure out how to formalize these situations (if anything, the answer is in Wikipedia ).
Algorithm X
Algorithm X consists of several steps that reduce the task to the original, but with fewer columns / rows. Moreover, it should be noted that the algorithm branches at a certain step. In other words, it is still busting, but smart :-)
Step 1. Select any column c in the matrix S
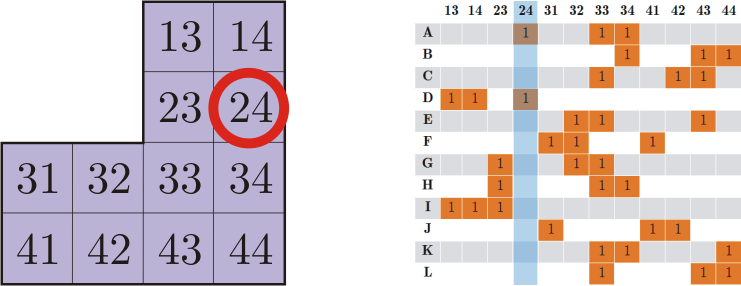
Selecting a column in a geometric language means selecting a square that has not yet been covered. In our case, it will be a square 24.
Step 2. Fork the algorithm for each row r , such that S r, c = 1
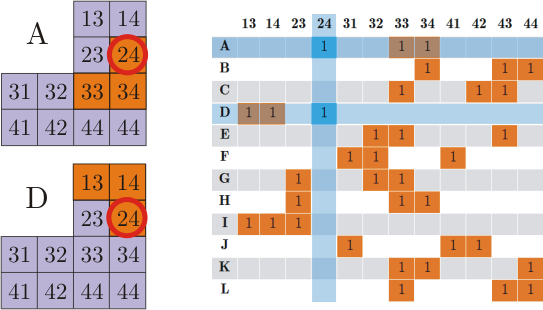
The square 24 can be closed both by position A and by position D. We have no prerequisites to choose this or that, therefore we consider both options separately. This is a step where options are searched. To reduce their number, often in step 1, they choose not an arbitrary column, but a column containing the smallest number of ones.
Step 3. For the selected row r , all columns j are considered , such that S r, j = 1
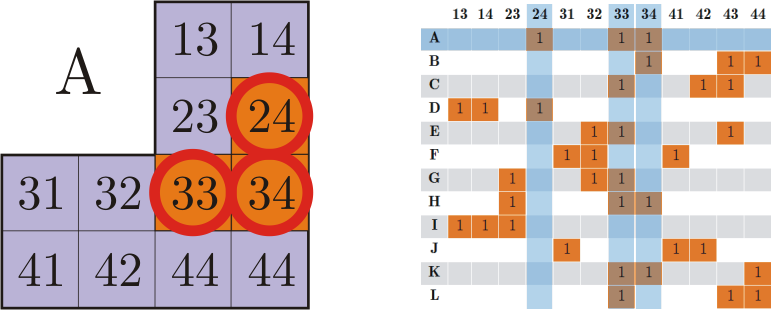
Select line A and put it on our solution stack. Now we need to select all the squares, which occupies the position A.
Step 4. For all nonzero elements of columns j, delete the rows in which they are located, and then the columns j themselves
All rows that have non-zero elements in the selected columns can no longer participate in the construction of this branch of the solution. In other words, we get rid of all the positions of the corner that intersect (have common squares) with position A. Moreover, since we have already covered squares 24, 33, 34 (row A is already on the stack), we do not need to take care of them next, and the corresponding columns are also deleted.
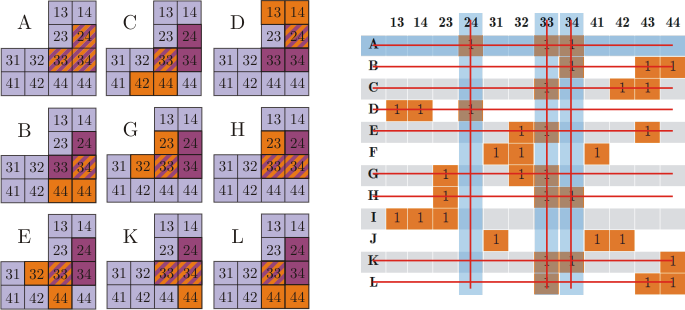
Step 5. Go to Step 1 with a reduced matrix.

After deleting the rows and columns, we got a smaller table. And from the point of view of geometry, we obtained the problem of covering a smaller figure, and the remaining lines automatically correspond to the possible positions of the corners in this figure.
Anecdote about the saucepan
Physics and mathematics are asked to boil water in a saucepan. Both solve the problem in the same way: they take water into a saucepan, put it on the stove and turn it on. After that, they are asked to boil the water that is already in the saucepan. The physicist puts the saucepan on the stove and turns it on. The mathematician pours water into the sink and says: "Now let's solve the previous problem."
End of algorithm
After the transition to step 1, we may have special situations.
Situation 1. We cannot select a column, because there are no columns left in the matrix. This means that we have covered all the available squares, therefore, we have found a solution to the problem. The contents of the stack can be added to the list of solutions found.
Situation 2. We chose a column, but there is not a single unit in it, for example, column 44 in the last picture. This means that for the selected square there is not a single position of the corner that could cover it. Therefore, this branch has no solution. A special case of this situation is that there are no rows left in the matrix. It is worth noting that by selecting the column with the smallest number of units in step 1, we will always get an empty column as soon as it appears.
Since, for the iteration of the algorithm, we deliberately get rid of one row and one column, the number of rows and columns decreases, and sooner or later we come to situation 1 or situation 2.
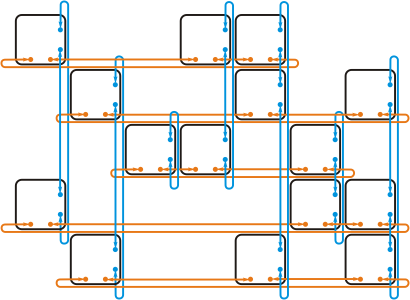
Dancing links
For fast operation of the algorithm, you must be able to quickly remove rows and columns from the matrix. If you store the matrix in the form of a two-dimensional array, then this is quite problematic. On the other hand, the resulting matrix is almost always very sparse (in particular, the matrix for the problem with pentamino contains only 4% of units), and therefore it is convenient to represent it as a two-dimensional doubly connected list. Such a representation allows us to obtain all nonzero elements of a row or column in the shortest time.
Finally, having such a list at your disposal, it is very convenient to delete columns and rows, and going back along the branch, restore them.
// node->next->prev = node->prev; node->prev->next = node->next; // node->next->prev = node; node->prev->next = node; It is on this idea that Knut's dancing links method is based. (By the way, if you type in Google the name of this method in the singular "dancing link", then there will be a lot of gifs with the main character Legend of Zelda in the pictures.)
Puzzle solution
The final solution code of the original puzzle can be viewed on the githab (most of the code is the preparation of the matrix and the function of checking solutions for identity). On my laptop, the program in 5 seconds finds 4 unique solutions (not turning to each other by turns and reflections) and for another 50 seconds makes sure that there are no others. It was nice to realize that your implementation is faster than the Burr Tools solution.
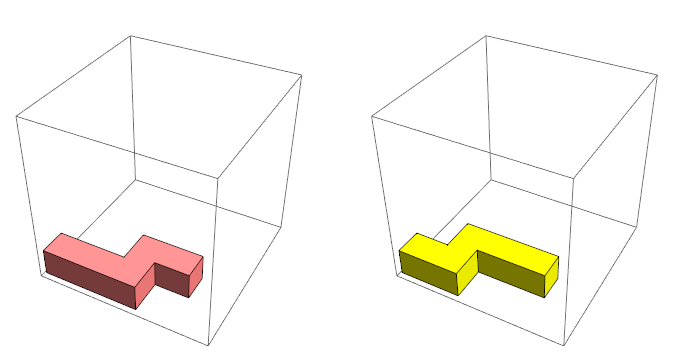
One of the optimization of the algorithm was to leave only 2 principal positions of the pentamen closing the cube (0, 0, 0), since its other possible positions are rotations and reflections. This reduced the number of brute force options by 6 times. (Actually, it is enough to leave one position, but this needs additional substantiation).
A solution to this (and other puzzles) can be found on puzzlewillbeplayed.com . And those who read to the end - a bonus in the form of visualization of a piece of the algorithm. Perhaps, this animation will justify the adjective “dancing” in the title of the algorithm.
Source: https://habr.com/ru/post/194410/
All Articles