Fractals in prime numbers

I discovered this fractal when I looked at the interference of waves on the surface of the river. The wave moves to the shore, is reflected and superimposed on itself. Is there any order in the patterns that are created by the waves? Let's try to find it. Consider not the whole wave, but only the vector of its movement. We will make the “beaches” smooth for the sake of simplicity of the experiment.

The experiment can be conducted on a regular piece of paper in a cell from a school notebook.

Or using a JavaScript implementation of the algorithm.
')
English version: New kind of fractals - Fractals in relatively prime integers (coprime integers)

Take a rectangle with sides q and p. Send a beam (vector) from corner to corner. The beam moves to one of the sides of the rectangle, is reflected and continues to move to the next side. This continues until the beam hits one of the remaining corners. If the size of the side q and p are mutually simple numbers, then a pattern is obtained (as we shall see later, a fractal).

In the picture we clearly see how this algorithm works.



Gif-animation:





The most amazing thing is that with different sides of the rectangle - we get different patterns.






Why do I call these patterns fractals? As is known, a “fractal” is a geometric figure with self-similarity properties. Part of the picture repeats the whole picture. If you significantly increase the size of the sides Q and P - it is clear that these patterns have properties of self-similarity.

Let's try to increase. Increase will be clever way. Take, for example, a 17x29 pattern. The following patterns will be: 29x (17 + 29 = 46), 46x (29 + 46 = 75) ...
One side: F (n);
The second side: F (n + 1) = F (n) + F (n-1);
17, 29, 46, 75, 121, 196, 317, 513, 830, 1343
As Fibonacci numbers, only with the other first and second term of the sequence: F (0) = 17, F (1) = 29.



















Further fractals cyclically repeat.

If the big side is even, we get this pattern:



If the smaller side is even:



If both sides are odd, we get a symmetric pattern:





Depending on how the beam begins:

or


I'll try to explain what happens in these rectangles.

Separate the square from the rectangle, and see what happens on the border.



The beam comes out at the same point from where it entered.



At the same time, the number of squares that the beam passes is always an even number.

Therefore, if you cut a square from a rectangle, then the unchanged part of the fractal will remain.

If you separate squares from a fractal as many times as possible, you can get to the “beginning” of the fractal.



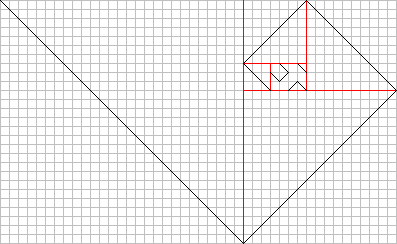
Looks like a Fibonacci helix?



You can also get fractals from Fibonacci numbers.

In mathematics, Fibonacci numbers (Fibonacci series, Fibonacci sequence) are numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 ...
By definition, the first two digits in the Fibonacci sequence are 0 and 1, and each subsequent number is the sum of the two previous ones.
F (n) = F (n-1) + F (n-2)
F (0) = 0, F (1) = 1



Go:




As we see, the closer the relationship of the parties approaches the golden section - the more detail is the fractal.



In this case, the fractal repeats part of the fractal, increased by .

Instead of Fibonacci numbers, you can use irrational sizes of the sides:



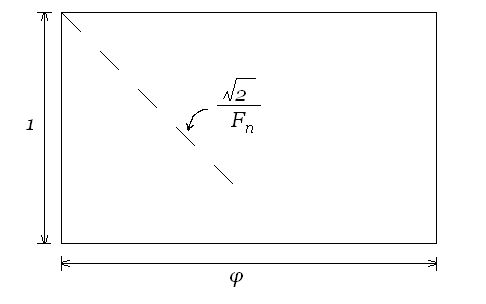
We get the same fractal.

The same fractals can be obtained in the square, if you shoot a beam from a different angle:



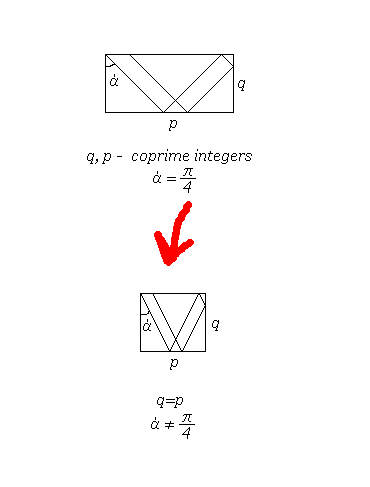
What can be said in conclusion?
Chaos is order too. With its own laws. This order is not studied, but quite amenable to study. And all the desire of science - to discover these patterns. And eventually combine the puzzle details to see the big picture.
Let's look at the surface of the river. If you throw a stone at her - the waves will go. Circles, fully amenable to study. Speed, period, wavelength - all this can be calculated. But until the wave reaches the shore, it does not reflect and does not begin to overlap with itself. We obtain chaos (interference), which is already difficult to study.
What if you move from the reverse? Simplify the wave behavior as much as possible. Simplify, find a pattern and then try to describe the full picture of what is happening.
What can be simplified? Obviously, to make the reflective surface straight, without bends. Further, instead of the wave itself, use only the motion vector of the wave. In principle, this is enough to build a simple algorithm and simulate the process on a computer. And even quite enough to make a "model" of the behavior of a wave on a regular piece of paper in a cell.
What do we have as a result? As a result, we see that in wave processes (the same ripples on the surface of the river) we have not chaos, but the imposition of fractals (self-similar structures) on each other.

Consider another kind of waves. As is known, an electromagnetic wave consists of three vectors - the wave vector and the vector of electric and magnetic field strengths. As you can see, if we “catch” such a wave in a closed area, where these vectors intersect, we get quite clear closed structures. Perhaps elementary particles are the same fractals?



All fractals in rectangles from 1 to 80 (6723x6723 px):


Closed areas in fractals (6723x6723 px):




Just a beautiful fractal (4078x2518 px):


If you have had the patience to read to the end, once again the JavaScript implementation of the algorithm :)