Harmonic search. Harmony Search
Preface
By feedback, it was decided to bring this post to mind, so I hope that now his reading will become a more pleasant and informative exercise. I tried to take into account all the wishes to the maximum.
Foreword
As I wrote earlier: there is a desire to cover heuristic methods (both fairly common and unknown). This post was intended to understand whether this topic will be interesting to you. Well, let's hope that I was not mistaken. The first method with which I would like to introduce the readers is the method of harmonic search (HS).
History reference
So, how did it all start? It all started not so long ago. In 2001, Geem developed and proposed its own harmonic search algorithm (Harmony Search, or HS). Some authors say that this algorithm was inspired by the game of jazz musicians, others say that it is just the process of creating a pleasant melody. Essentially it does not change. The only important thing is that an experienced musician can quickly both play with other musicians and improvise something beautiful. This formed the basis of the algorithm.
')
Strategy
Classic HS uses the concept of harmonic memory (by analogy with the parent pool of genetic algorithms). Here are stored vectors representing approximate solutions to the optimization problem. Initially, they are randomly generated in an area that is examined for the presence of a maximum or minimum (depending on what you need). The size of this memory is naturally limited. Next comes the
The improvisation itself is as follows:
- a test vector is generated (either completely randomly or using memory vectors),
- the trial vector is modified (there is a slight shift in the components, if the trial vector was created using memory),
- the modified test vector replaces the worst in memory.
For those who are interested in a more detailed description of the algorithm
The plan of the algorithm itself was treacherously taken from [ 3 ]. Add a few formulas to make it all take a more meaningful look. So, we have some function
that needs to be minimized and the scope of the search 
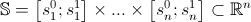(for simplicity, we assume its multidimensional rectangular parallelepiped), in which the minimum point, or rather its approximation, will be searched. The next step is to generate the initial harmonics in our search area. 
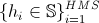(randomly). Magnitude 
is set by the user, and, as it is easy to guess, indicates the number of harmonics that can be stored in memory. In addition, the user must also specify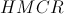 
- the probability of choosing from the harmonics in the memory, 
- probability of modification and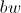 
- the value of the modification itself. Now that all the preparations have been made, with a clear conscience we can proceed to create music to minimize the function. The iterative part continues until the stopping criterion of the algorithm is satisfied. It can be either a limit on the number of iterations, or the number of runs without updating the harmonic memory, or the proximity of the added harmonics in the sense of a particular metric. It all depends on your desire. During the iterative part, the following happens:
Algorithm
The plan of the algorithm itself was treacherously taken from [ 3 ]. Add a few formulas to make it all take a more meaningful look. So, we have some function
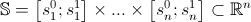that needs to be minimized and the scope of the search (for simplicity, we assume its multidimensional rectangular parallelepiped), in which the minimum point, or rather its approximation, will be searched. The next step is to generate the initial harmonics in our search area. 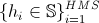(randomly). Magnitude is set by the user, and, as it is easy to guess, indicates the number of harmonics that can be stored in memory. In addition, the user must also specify 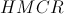- the probability of choosing from the harmonics in the memory, 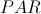- probability of modification and 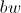- the value of the modification itself. Now that all the preparations have been made, with a clear conscience we can proceed - Create a zero harmonic
. - Next, for each harmonic component, do the following: generate a random number
uniformly distributed from zero to one. If a less than 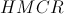then in the current component write the corresponding component from randomly selected harmonics from the memory. Otherwise, the component is generated randomly, taking into account the belonging to the corresponding component of the search area. 
. If the component was generated using memory, then it may be subject to modification. For this, a random number is generated again. uniformly distributed from zero to one. If a less than 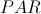, the component changes by 
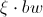where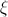 
- random variable uniformly distributed from 
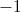before 
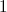. - If a
then 
replaces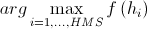 
(memory update is in progress).
Pros and cons
Pros:
- simplicity (both implementation and understanding). Indeed, the algorithm is not piled up with operations (in fact, only the generation of random numbers and modification of the vector);
- a sufficiently small number of adjustable parameters and the availability of recommendations on the choice of parameters;
- is a method of zero order (there is no need for numerical differentiation, and, therefore, all the complications associated with this process);
- the method is easily and conveniently incorporated into other methods (for example, in memetic algorithms, or as an additional contour of the genetic algorithm).
Minuses:
- low convergence rate;
- In my opinion, the method is poorly applicable to solving problems of large dimensions (like the simulation method of annealing) because of the simplicity of the operations that compose the method (in this case, the same genetic algorithms work an order of magnitude faster).
Used sources
- Zong Woo Geem, Music-Inspired Harmony Search Algorithm (Springer Publishing),
- Wikipedia
- An article by Chukiat Worasucheep (there are links to HS variations),
- Article by Xin-She Yang, one of my favorite authors and scholars.
Afterword
I want to make a good tradition - to determine the topic of the future post by voting. So please all not indifferent vote for the topic of the next post.
Source: https://habr.com/ru/post/193994/
All Articles