Normal numbers: educational program
Not so long ago, I came across a great humorous article about a file system that stores data in Pi . The heated discussion in the comments (it seems that not all of the participants understood the joke) suggested me that the topic of normal numbers would be nice to discuss more seriously, especially since this topic is fertile, full of beautiful results, unsolved problems and other kosher things. If you want to get acquainted with these things - please come under cat.
')
Numbers suitable for “storing”child pornography and unlicensed content in them; arbitrary data by means of a method resembling a book cipher are called disjunctive . More strictly, a number is called disjunctive in base b if its b-ary record contains any finite sequence of b-ary digits. Such numbers are easy to build artificially. For example, we write out all natural numbers in a row as the fractional part of the decimal disjunctive number:
A slightly less “artificial” disjunctive number can be obtained as the sum of a series: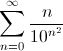
that would look like:
Or, using the result I obtained here , as well as reducing the number of extra zeros, you can take the sum of our "Babylonian library"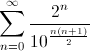
which looks like this:
Similar constructions can be used to construct disjunctive numbers on an arbitrary base.
A lexicon , or an absolutely disjunctive number, is a number disjunctive on any basis. If the usual disjunctive number is the Babylonian library, then the lexicon can be called the “Babylonian Wikipedia” containing the Babylonian library in each language section (number system).
Such a thing is more difficult to design. However, as the prophetic Oleg used to say, “my horse is not afraid of dangerous labors”. The idea is as follows: each b-digit number can be slightly increased by some Δ so that its first k digits remain unchanged (b and k are any). Moreover, for several number systems, one can choose some Δ min so that with an increase on it the first k numbers in any of these number systems would not suffer. Therefore, to build the lexicon L, you can use the following algorithm:
You can try to trace the first few steps of this algorithm.
A normal number by base b is such a disjunctive number (by the same basis), that for every k all sequences of b-ary digits of length k are included in the b-ary record of this number with the same asymptotic density b -k . By the asymptotic density of the sequence w is meant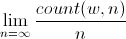
where count (w, n) is the number of times the sequence w occurs among the first n digits.
Speaking of workers and peasants, a number is normal if in a sequence of its numbers all subsequences of equal length occur equally often. In the context of our hypothetical file system, this means that identical data volumes will have displacements of approximately the same order. If we discard the jokes aside, on average, the offset entry will be approximately the same length as the information encoded by this offset. So no compression 100%, alas.
Similar to the concept of an absolutely disjunctive number, there is also the concept of an absolutely normal number . As you might guess, this number is normal for any reason.
Surprisingly, all the numbers we deal with in everyday life are not normal. "Abnormality" of integers is obvious - their fractional consists of only zeros. The rational numbers are also abnormal, since their fractional part at some point becomes periodic, and we can choose a sequence of numbers, which with this periodicity is in tight disagreement.
As for the irrationality familiar to our eyes (pi, e, the root of two, etc.) - with them, too, everything is far from smooth. British scientists believe these numbers are normal; but today, to my knowledge, there is not even evidence that they are disjunctive.
It turns out that we do not know a single "adequate", naturally obtained normal number. What then is normal in them? The answer is simple: the majority of normal numbers. It is proved that the set of "abnormal" numbers has a Lebesgue measure 0. This means that if you stick your finger at a single segment, then with a probability of 100% you will get a normal number.
There are two significant differences between normal and disjunctive numbers. The first is an additional condition imposed on the asymptotic density of sequences of digits in the normal number record. The second is that the very existence of normal numbers is less obvious.
Let us return to the examples of disjunctive numbers from the “Babylon Library” section. It is easy to understand that the second and third examples are not normal: in them the asymptotic density of zero will be significantly higher than that of other numbers. I will tell you a secret:
But the first example, oddly enough, is a normal number. By the way, this number is called the Champernoun constant . Also the Copeland-Erdös constant is normal:
- consisting of decimal entries of prime numbers. It is proved that similar constants are normal in other number systems. The normality of such numbers as:
- and many others. However, the proofs of their normality are not trivial. In the next article, if this topic interests the habrasoobshchestvo, I will show how to build a number, the normality of which is obvious. This will require a separate article, since the way of its construction is rather unobvious (and interesting!). It seems that there is a certain analogue of the Heisenberg uncertainty principle concerning the complexity of constructing a normal number and the difficulty of proving its normality :)
As for the absolutely normal numbers - for them, unlike lexicons, there is not even a construction algorithm. However, it is proved that the algorithm exists. So it goes.
There is a possibility that the Pi number will not ensure the proper safety of your files. I recommend using any artificially derived normal number instead, for example, the Champernoun constant. By the way, a rather interesting algorithmic task is to determine the index of its first entry in the decimal notation of this constant for a given sequence of digits.
That's all. Goodbye, girls and boys, until we meet again, and let everything be normal with you.
')
Babylon Library
Numbers suitable for “storing”
0.12345678910111213 ...
A slightly less “artificial” disjunctive number can be obtained as the sum of a series:
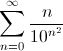that would look like:0,1002000030000004 ...
Or, using the result I obtained here , as well as reducing the number of extra zeros, you can take the sum of our "Babylonian library"
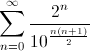which looks like this:1.204008001600032 ...
Similar constructions can be used to construct disjunctive numbers on an arbitrary base.
Lexicon
A lexicon , or an absolutely disjunctive number, is a number disjunctive on any basis. If the usual disjunctive number is the Babylonian library, then the lexicon can be called the “Babylonian Wikipedia” containing the Babylonian library in each language section (number system).
Such a thing is more difficult to design. However, as the prophetic Oleg used to say, “my horse is not afraid of dangerous labors”. The idea is as follows: each b-digit number can be slightly increased by some Δ so that its first k digits remain unchanged (b and k are any). Moreover, for several number systems, one can choose some Δ min so that with an increase on it the first k numbers in any of these number systems would not suffer. Therefore, to build the lexicon L, you can use the following algorithm:
- First, take L = 0.
- For each n from 2 to ∞, perform step 3.
- For each b from 2 to n, perform step 4.
- Increase the number L by such a minimum Δ so that in the b-ary number system its record will contain a b-ary record of the number (n - b + 1), but at the same time not a single record made by previous iterations of this item will be “erased”.
- Make the limit
- Profit!
You can try to trace the first few steps of this algorithm.
But it is unsafe for the psyche ...
First, the algorithm will write one into the “binary section” of the lexicon. It turns out (0,1) 2 , i.e. 1/2. Then he writes a two in the binary section, i.e. (10) 2 . It turns out (0.10) 2 - the number has not changed in fact, Δ = 0, but the second decimal place in the binary number system is now “reserved” and cannot be changed by the subsequent steps of the algorithm. Next we must write the unit in the ternary section. (0,1) 2 = (0,11111111 ...) 3 , no increase is required, but we reserve the first ternary decimal place. Now we write a three in the binary section, we get (0,10011) 2 = 19/32 (note that if we took (0,1011) 2 , it would change the first three-digit character, which is already reserved). And so on ad infinitum.
Shake normal
A normal number by base b is such a disjunctive number (by the same basis), that for every k all sequences of b-ary digits of length k are included in the b-ary record of this number with the same asymptotic density b -k . By the asymptotic density of the sequence w is meant
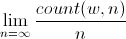where count (w, n) is the number of times the sequence w occurs among the first n digits.Speaking of workers and peasants, a number is normal if in a sequence of its numbers all subsequences of equal length occur equally often. In the context of our hypothetical file system, this means that identical data volumes will have displacements of approximately the same order. If we discard the jokes aside, on average, the offset entry will be approximately the same length as the information encoded by this offset. So no compression 100%, alas.
Similar to the concept of an absolutely disjunctive number, there is also the concept of an absolutely normal number . As you might guess, this number is normal for any reason.
Abnormal normality
Surprisingly, all the numbers we deal with in everyday life are not normal. "Abnormality" of integers is obvious - their fractional consists of only zeros. The rational numbers are also abnormal, since their fractional part at some point becomes periodic, and we can choose a sequence of numbers, which with this periodicity is in tight disagreement.
As for the irrationality familiar to our eyes (pi, e, the root of two, etc.) - with them, too, everything is far from smooth. British scientists believe these numbers are normal; but today, to my knowledge, there is not even evidence that they are disjunctive.
It turns out that we do not know a single "adequate", naturally obtained normal number. What then is normal in them? The answer is simple: the majority of normal numbers. It is proved that the set of "abnormal" numbers has a Lebesgue measure 0. This means that if you stick your finger at a single segment, then with a probability of 100% you will get a normal number.
Normal vs Disjunctiveness
There are two significant differences between normal and disjunctive numbers. The first is an additional condition imposed on the asymptotic density of sequences of digits in the normal number record. The second is that the very existence of normal numbers is less obvious.
Let us return to the examples of disjunctive numbers from the “Babylon Library” section. It is easy to understand that the second and third examples are not normal: in them the asymptotic density of zero will be significantly higher than that of other numbers. I will tell you a secret:
Hidden text
the asymptotic zero density in these examples is 1. The farther we go from the integer part, the less likely it will be to meet any other digit. In the limit, this probability can be neglected, saying that the record consists of zeros almost completely.
But the first example, oddly enough, is a normal number. By the way, this number is called the Champernoun constant . Also the Copeland-Erdös constant is normal:
0.235711131719 ...
- consisting of decimal entries of prime numbers. It is proved that similar constants are normal in other number systems. The normality of such numbers as:
0.1491625364964 ...
0.182764125216 ...
0.1361015212836 ...
- and many others. However, the proofs of their normality are not trivial. In the next article, if this topic interests the habrasoobshchestvo, I will show how to build a number, the normality of which is obvious. This will require a separate article, since the way of its construction is rather unobvious (and interesting!). It seems that there is a certain analogue of the Heisenberg uncertainty principle concerning the complexity of constructing a normal number and the difficulty of proving its normality :)
As for the absolutely normal numbers - for them, unlike lexicons, there is not even a construction algorithm. However, it is proved that the algorithm exists. So it goes.
Summary
There is a possibility that the Pi number will not ensure the proper safety of your files. I recommend using any artificially derived normal number instead, for example, the Champernoun constant. By the way, a rather interesting algorithmic task is to determine the index of its first entry in the decimal notation of this constant for a given sequence of digits.
That's all. Goodbye, girls and boys, until we meet again, and let everything be normal with you.
Source: https://habr.com/ru/post/193936/
All Articles