About automating chord selection
I have long been interested in the question: “what if I tried to get rid of the digital recording of a song through the Fourier transform, look at the dependence of the spectrum on time and try to pull out the chords of the song from the information received?”. Here, finally, I found the time to try ...
So, the statement of the problem:
There is a file with digitized music (not MIDI!), For definiteness mp3. It is necessary to determine the sequence of chord changes, forming the harmony of the piece. By "music" we will mean typical European music - 12 semitones in an octave, harmony mainly based on major / minor triads, also reduced and increased triads and * sus2 / * sus4 are acceptable (chords with 2nd / 4th step instead of 3 th)
Notes in European music are sounds with frequencies from a fixed set (more on this below), and sounds that differ in frequency of 2, 4, 8 ... are indicated by one note. Musical intervals are fixed frequency ratios of two notes. This interval system is organized as follows:
The letter designations of the notes in the notation adopted in Russia are:
A - A, B - B-flat, H - B, C - C, D - D, E - M, F - F, G - Sal.
# (sharp) indicates an increase in frequency by 1/2 tones, b (flat) - a decrease by 1/2 tones. Per octave of 12 semitones, the notes are displayed as follows:
ABHCC # / Db DD # / Eb EFF # / Gb GG # / Ab
')
Octaves have tricky names and numbers, but we are not interested, it is enough to know that the frequency of the “la” note of the first octave is 440 Hz. The frequencies of the remaining notes are easy to calculate, based on what was written above.
A chord consists of several simultaneously sounding notes. At the same time, they can be extracted sequentially (arpeggio, it is “busting” in the jargon of yard guitarists), but since the sound does not calm down immediately, the notes have time to sound together for a while. In the European tradition, the most common chords of the three sounds (actually triad). Major and minor triads are commonly used. In major chords, the 1st (starting from the lowest) and 2nd notes form a large third, and the 2nd and 3rd ones form the minor third, while in the minor, the 1st and 2nd ones form the minor, 2nd and 3rd is great. The 1st and 3rd notes in both cases form a fifth. There are also reduced (two small third) and increased (two large third) triads, and in rock music, sustained-chords are quite common (I don’t know how they are in Russian) - sus2 with a 2 nd note for 1/2 tone lower than that of the minor and sus4 with a 2 nd note ½ tones higher than that of the major. The 3rd note in both versions of the sustained-chord forms the 1st ordinary fifth.
In a single piece of music, it is rarely when all 12 notes are used equally. As a rule, there is a “base” subset of 7 notes, and notes are taken mainly from it. Such a subset can be defined using a mask of 0 and 1, superimposed on a vector of 12 notes. If to exaggerate, such a subset is called a tonality, and the set of all possible cyclic shifts of a tonality mask is called a fret. In European music, two frets are mainly used:
The chords used in a particular key are constructed, to the extent possible, from the notes of that key.
You may notice that the masks of major and minor differ to the accuracy of the shift. Accordingly, the chords, for example, in C major and the corresponding A minor, are used the same (it was we who so unobtrusively returned to our task).
The note “from which” the mask was applied was called tonic. The number of the note entering the key, starting with the tonic, is called the degree. When talking about the structure of a particular chord, the steps are counted from its 1st note (the so-called pitch).
Chords are traditionally denoted by the symbol of its pitch, to which a chord type suffix is assigned to the right without a space. For example, note A (A):
[Offtopic for those who studied in the "muzykalka"] I heard about the differences between the melodic and harmonic minor and about the problems of temperament (going back to the roots of the 12th degree) too. But, as it seems to me, in the framework of this article, the above simplified description of the subject area is sufficient.
So, we need:
I didn’t bother with the first task - I took a ready sox sound converter that supports both mp3 and “raw” formats, where the sound is stored just like a graph of the amplitude versus time. In * nix-systems, it is trivially set using the package manager - on Ubuntu it looks like this:
$ sudo apt-get install sox
$ sudo apt-get install lame
The second line puts the LAME mp3 encoder.
Under Windows, sox can be downloaded from the official site, but then you have to suffer a little with searching the Internet for suitable LAME DLLs.
With the second task, in principle, everything is simple. In order to understand which notes sound at a particular point in time, it is necessary to perform a spectral analysis of a piece of our array with amplitudes in the range of indices corresponding to a small neighborhood of this moment. As a result of spectral analysis, we obtain amplitudes for a variety of frequencies that "compose" the analyzed piece of sound. It is necessary to filter the frequencies, highlighting those of them that are close to the frequencies of the notes, and select the largest of them - they correspond to the loudest notes. I say “close,” not “equal,” because in nature there are no perfectly tuned musical instruments; This especially applies to guitars.
For spectral analysis of a discrete representation of a time-varying signal, you can use the window fast Fourier transform. I tore the simplest non-optimized FFT implementation from the Internet, translated it from C ++ to Scala, and took the Hanna function as a window function. More about this all can be read in the relevant articles of Wikipedia.
After receiving an array of amplitudes by frequency, we select frequencies in the vicinity (its default size is 1/4 semitones) around the frequency of each note in a certain octave range (experience shows that it is best to analyze octaves with a large second or third). In each such neighborhood, we calculate the maximum amplitude and consider it as the loudness of the corresponding note. After that, we summarize the “loudness” of each note by all octaves and, finally, we divide all the elements of the resulting array of 12 “loudnesses” by the value of its maximum element. The resulting vector of 12 elements in different sources is called a chromogram (chromagram).
Here it is impossible not to mention a pair of subtleties. Firstly, for different works the convenient range of octaves for analysis is different - for example, the introduction to My Friend Of Misery Metallics is played, apparently, on a bass guitar and sounds quite low; in the upper octaves, there are mostly overtones and left frequencies from the distortion, which only interfere.
Secondly, there are no perfectly tuned guitars in nature. This is probably due to the fact that the strings depending on the frets are differently extended during clamping (well, in general, the fingers put uneven pressure on them). In addition, this tool quickly gets upset in the process of playing on it. For example, in the acoustic recordings of Letov with the setting of the full finish - well, this can be understood. But why, in the same My Friend Of Misery, one not-remember-which note stably sounds exactly a quarter of a tone, not that higher, not that lower — a mystery. And even with well-tuned guitars on the records of all kinds of home-based artists, the line usually does not coincide with the canonical one in terms of total height — i.e. The “la” of the first octave may not be exactly 440 hertz.
In order to neutralize such shoals, it was necessary to envisage in the program the possibility of compensating for a general shift in the order. But with the frustration of individual strings and, in general, the indispensable “inconvenience” of guitars can not be helped. So ambush with the main rock instrument.
[Another Offtopic] The set of songs that will be mentioned in this, so to speak, “essay” may seem somewhat wild. However, the selection criteria were very simple:
That is, I tried to simplify my life, at least at the beginning of torment with the selection of each song.
But back to our three tasks.
The remaining, third, task seems trivial - we select the three loudest notes and add a chord out of them. But in reality, this will not work (well, not quite anything - see below, but there is very little sense from this approach). And in general, this task was the most difficult of all.
Now about everything in order.
At first, I did exactly as described above - after analyzing each “window” of the sound file I selected the three loudest notes and tried to make a chord out of them.
The first composition in which I tried to experience the magical effect of my miracle program was “Judas will be in paradise” by Letov in the variant from the Tyumen bootleg aka “Russian Field of Experiments (Acoustics)”. Vstulenie to this song is a dolbyob on a minor triad for about ten seconds.
However, having banished my program at the beginning of this song, I did not find a single (!) Chord Em in the output. Basically nothing was determined; occasionally any completely “left” nonsense climbed. What was the matter, it was not clear. I had to implement a private dump of each window in the form of a histogram of '*' symbols. From the histogram, first of all, it turned out that the structure of the guitar differs by about a quarter of a tone from nominal. OK, we introduce the amendment. Hooray! The notes E and H began to be determined - the 1st and 3rd in the chord. But where is G?
Further investigation of the dump revealed the following:
Apparently, therefore, G rarely even turns out to be in 4th place.
In general, I scored on the selection of Letov. And in general, it became clear that we need to look for another way to analyze the chromogram. But, in fairness, I must say that there exists in nature at least one fragment, which is normally chosen in this way. This is an introduction to the song of Olga Pulatova “Pink Elephant”, which is an arpeggio on electronic keys. The program on it produced the following result (after manual cleaning of artifacts formed at the junctions of chords and removing consecutive repeats): Fm Cm (c db f) Ab Abm Eb Ebm B. ((c db f) - non-standard consonance, which without special damage may be replaced by Db). An independent check shows that the chords are correct.
Here it is, the power of a blunt piece of iron! With the hands of Olin delicacy with three tonalities for 8 chords, you can select a long and unsuccessfully ... But, alas, I repeat, this is the only composition I know that is successfully analyzed in this way. The reasons for the failure are understandable - on the one hand, the overtones and “left” frequencies of the guitar “lotions” interfere, on the other hand, the chords rarely sound by themselves, over them with higher, and the loudness usually includes the melody - vocals, guitar / keyboard solo and t .P. Melody rarely fits completely into harmony on notes - it is too sad, as a result, “temporary” harmonies are constantly formed in the stream of sound that do not correspond to any canonical chords, and everything breaks.
I had to go to Google and dig. The topic turned out to be quite popular in the scientific and near-scientific environment, and in nature there is something to read about it, if you are not afraid of terms like hidden Markov model, naive bayesian classifier, gaussian mix, expectation maximization etc. At first I was afraid to climb into all this jungle. Then figured out on the sly.
Here is the article that turned out to be the most useful for me:
http://academia.edu/1026470/Enhancing_chord_classification_through_neighbourhood_histograms
To begin with, the authors propose not to look for exact matches with chords, but to evaluate the degree of “proximity” of the chromogram to the chord. They offer three ways to assess such proximity:
After a few more detailed studies from other sources, I threw the third way out - he, judging by the conclusions from the above article, gives results a little better than the trivial first method, and hemorrhoids with matrix arithmetic, calculation of determinants, etc. lot.
But the first two I implemented.
The first way is super simple. Suppose we have a chord (for definiteness Am) and a chromogram. How to determine how the hromogram "similar" to the chord?
We take the mask of notes that sound in a chord - like the one we drew for the key. For Am, it will be 1 0 0 1 0 0 0 1 0 0 0 0. We multiply this mask as a scalar by the chromogram, as if they were 12-dimensional vectors (well, that is, we stupidly summarize the elements of the chromogram with those indices that are marked by one in the mask) . Voila - here it is, a measure of "similarity." We look through all the chords that we know, we find the one with the “similarity” the biggest - we believe that it sounds.
The second method is slightly more difficult to implement, but requires training data. It is based on the Bayes theorem. "On the fingers" it looks like this.
There is a concept of conditional probability: conditional probability P (A | B) is the probability of an event A , provided that event B has occurred. This value is determined by the following identity: P (AB) == P (A | B) * P (B) , where P (AB) is the probability of the joint occurrence of events A and B.
From here:
P (AB) == P (A | B) * P (B)
P (AB) == P (B | A) * P (A)
That is, under the condition of nonzero P (A)
P (B | A) == P (A | B) * P (B) / P (A)
This is the Bayes theorem.
How do we use it? Let us rewrite the formulation of the theorem in convenient notation for our problem:
P (Chord | Chroma) = P (Chroma | Chord) * P (Chord) / P (Chroma) ,
where Chord is a chord, Chroma is a chromogram
If we learn from somewhere the distribution of chromograms depending on the chord, then we can find the most plausible chord for a given chromogram, by maximizing the piece P (Chroma | Chord) * P (Chord) - since the chromogram is given, and P (Chroma) , so constant.
It remains to understand where to get the distribution of P (Chroma | Chord) . For example, you can let the program “listen” to the recordings of specific known chords so that it can estimate these distributions based on them. But there is a nuance. The probability of obtaining a specific value of a chromogram in the “training” examples is negligible - simply because there are very many possible values. As a result, when using learning results for real work in the overwhelming majority of cases, P (Chroma | Chord) will be zero for all Chord values, and there will be nothing to maximize.
It is possible (and necessary) before classification to simplify chromograms, for example, by dividing the range of relative amplitude [0, 1], on which the components of the chromogram are defined, say, 3 parts (with the meaning “almost as loud as the loudest note”, “several quieter than the loudest note "," very quiet compared to the loudest note "). But still there will be too many options.
The next thing you can do is to assume that the probability distribution of each component of the chromogram is independent of the other components. In this case, P (Chroma | Chord) = P (c 1 | Chord) * ... * P (c 12 | Chord) , where c 1 .. c 12 are components.
chromograms, and for this particular case we obtain the following formulation of the Bayes theorem:

But P (c i | Chord) can already be extracted even from a scant amount of training data - if, of course, the chromogram is “simplified” by limiting the definition of ci to three values, as we agreed above.
It remains to take P (Chord) from somewhere for all the chords in question. It does not matter - any collection of songs with chords will do for this, the main thing is that there are a lot of songs and they are different authors.
A classifier based on maximizing the expression P (c 1 | Chord) * ... * P (c 12 | Chord) * P (Chord) using the Chord parameter is called a naive Bayesian classifier. And in this particular case, its “naivety” is essential, since in reality the components of the chromogram are dependent random variables - for example, due to the same overtones. However, as we will see later, this approach works.
All this is easily realized - the code of the classifier itself and the “subsystem” of its training is far less than the description given here. I taught him on a set of major and minor piano chords from some free samples website and a compilation of an original song of the 90s with chords (the first thing that was found on the Internet as a single text file).
Now about the results of field trials. In the tests participated, in addition to the already mentioned My Friend Of Misery and “Pink Elephant”, the following compositions:
What happened. Both classifiers work very hard, all the while jumping from chord to chord. Naive Bayes are slightly more stable than the maximum of the scalar product, but it seems that only because it “knows” less chords (only major and minor). Since he, in contrast to the “scalar” brother, “knows” the probabilities with which different chords occur in the author’s damn song of the 90s, he behaves somewhat bydlovato, trying, roughly speaking, to shove the “three thugs” everywhere . Glimpses of reason are found in both classifiers, but for some reason, as a rule, on different fragments of the same work. Best of all, they coped with Misery. Bayes periodically fairly consistently gave out Dm and Am locomotives, which is correct (there is Dsus2 / E type harmony Am / E many, many times; / E is with bass "mi" in the sense). The “scalar” classifier who knows too many chords randomly wandered between Dsus2, Asus2 (aka Dsus4), D, Dm, D5 + and the left trash trying to recognize Dm, and behaved in the same way on Am.
Something managed to pull out of the "In a dream." Despite the poor sound quality, it was possible to manually identify the almost correct chords of the entry Cm Eb Bm (actually, the last chord B, as it should be in C minor) and the verse Cm Gm Cm Gm Ab F Ab F. The second, “decorated” part of the entry drowned in the garbage (looking ahead - I never picked it up, the more advanced classification methods also give out nonsense).
From “Soldiers Are Not Born,” they didn’t manage to get anything at all ... I don’t understand why. In the dump spectrum garbage. But it sounds normal to hear and pick up by hand is quite possible - Am CGH is there in the introduction, however, I’m not sure about tonality - the famous beast has arrived in the ear).
Naive Bayes coped better with “Assol”. He clearly liked the CSP-shnaya harmony in the d-minor, and glimpses of reason he happened quite often - he picked up the percentages of 20-25 chords correctly, which is against the general sad background and taking into account the “cunning” chords Comrade. Chigrakova not bad. But why did he replace almost all A on F # and F # m? Nonconformist, however.
In general, it was clear that we need to dig further.
Why do the above methods work so badly? If you know how to play something, imagine that you are offered to pick up a song, playing separately fragments in length of half a second, and not in order, but separately, so that you could not take into account the already selected part when working with the next “quantum”. Will you have something? I would venture to suggest that even if you have absolute hearing, the result will be deplorable.
Therefore, the authors of the above-mentioned work (as well as other similar studies) suggest using musical knowledge as they are expressed by evaluating the “similarity” of a chromogram to different chords. They have this secret knowledge that the probability of meeting one of the chords, which has already been encountered in the composition (or rather, in some of its time window), is higher than this probability for previously unseen chords. At the same time, they take into account the "fuzziness" of recognition of chords, the frequency of their occurrence in the analyzed window, etc.
In general, this is equivalent to such empirical knowledge "Songs are usually written in one, maximum two tonalities, and therefore the set of chords used in them is limited."
I decided to go a little different way. I proceeded from the following:
With this assumption, you can use Markov chains to simulate the process of changing chords.
Imagine a system with a finite (or infinite but countable, i.e. "numbered") the set of states S . Let it “live” in discrete time, which has an initial “0th” moment and then each moment of time can be designated by its number - t 1 , t 2 , etc. Let given probability distribution for the initial state of the system P 0 (S i ) and transition probabilities P (S (t n ) = S i | S (t n-1 ) = S j ). Such a random process, when the probability of a system transitioning to a specific state depends only on its current state, is called a Markov chain (in our case, with discrete time). If the transition probability distribution does not depend on the time t n , the Markov chain is called homogeneous.
I nadergal distribution of the first chord and transitions from a heap of songs, unpacking 40-megabyte chm-nickname with the name like "all Russian rock with chords." However, the authors “drive” - there are no chords there even for some Cinema and Crematorium albums, not to mention such exotic as Pulatova (there are texts, interestingly, there are). Still, the array of collections is quite large, so we can assume that the sample is representative enough to estimate the parameters of our Markov chain. Analysis of the songs was from 10 pm to at least 5 am the next day, however, on the "atomic" netbook.
Go ahead.Remember the Bayes theorem - P (Chord | Chroma) = P (Chroma | Chord) * P (Chord) / P (Chroma) ? With the help of our Markov chain, we will evaluate P (Chord) , and P (Chroma | Chord), let it still be evaluated by naive Bayesian and "scalar" classifiers. Regarding the latter, we, in fact, don’t need a “real” probability, so we can consider our inner product for chromogram to chord mask as “probability” that this chromogram corresponds to this chord. Well, you can also normalize these scalar pieces so that their sum over all chords is equal to 1, although it is not necessary to search for the maximum, and I scored them.
So we can estimate P (Chord (t 0 ) = C i ), based on the statistical evaluation of the distribution of the first chords in the Russian rock compilation (in this way, we take into account the actually different frequency of using different tonalities). For the next windows, we can evaluate P (Chord (t n ) = C n ) as
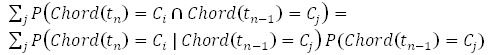
where P (Chord (t n-1 ) = C j ) were evaluated at the previous step. Find the maximum value of this expression for all i and get the most likely chord. Please note - here we take into account the fact that we do not know for sure what chord sounded in the previous window, we only have an estimate of the probability distribution of different chords.
As for the probability of “not moving” from chord to chord, I added the corresponding command line parameter and select the optimal value manually. In fact, this probability depends on the ratio between the duration of the stream window being analyzed and the musical tempo of the piece.
The above algorithm with proper selection of parameters proved to be very stable. Stumbling off the right path when trying to “bydolofikatsii” some difficult harmony, he honestly tries to return from the split ball, and most often he succeeds.
Optimization number 1. It was noted that the classifier "blows the roof", as a rule, on different fragments. It is also noted that if the same chord defined the classifier several times in a row, this chord is usually correct. These observations led to the following optimization: we start the ring buffer for several chords and push the chords there from the output of both classifiers. If once again the classifiers gave out different chords for the same window, take the one that occurs more often in the buffer (well, if it is equally common or not at all, then the first of the two).
Optimization №2.Different tonalities are used in music (especially guitar, where the fingering depends on them) with different frequencies. Basically, the people, of course, love those who have fewer alteration icons in the key — that is, in A minor / C major, E minor / G major, D minor / F major, or in the extreme case of B minor / D major.
Because of this, the statistics on transitions between chords for the most common keys are “better” than for less common ones. Hence the possibility of the possibility of “virtual transposition” —the command line keys that say the program “pick up chords in the tone that you see, but take the transition probabilities as if everything sounds n / half lower / higher”.
This approach is often used in manual selection - for example, we know that the song is in C minor, but we pick up chords in A minor, mumbling a melody a half tone lower, because what are the chords in this C minor? and the fingers keep the barre tired all the time.
The results of this stage are as follows: when applying the approach described above with both optimizations, we managed to find chords for the songs of O. Pulatova “In a dream” (except for the second part of the introduction) and “The river of times” (introduction and verse; tonality is a certain mixture of ly minor) with the accuracy of selection of about 70% or even slightly more. Hooray!
As for the second half of the introduction to "In a dream" - the best implementation, apparently, will be to go to Odessa, by chance there meet the author, ask her for chords, hardcore.
The Viterbi algorithm allows using indirect data (well, that is, in our case, chromogram) for a certain period of the Markov chain’s life, to obtain the most likely sequence of states (chords) that the process has gone through during this period. The algorithm is very simple, and I tried to implement it, but, I see, I do not know how to prepare it. Depending on the likelihood of “not moving,” it either sticks on one chord, or gives out a bunch of garbage (though usually in the right tone). Perhaps this is due to the requirement that “the results of the observations should be 1-to-1 correspond to the“ steps ”of the random process passed.” But, on the other hand, who prevents us from believing that our “step” has a fixed physical lifetime, and then the next step comes, even if the state has not changed? I do not know.Or maybe just somewhere there are errors in the code - debugging such things is not easy ...
Well, that's all. Thanks for attention!
Sources can be taken here: https://github.com/t0mm/ChordDetector
So, the statement of the problem:
There is a file with digitized music (not MIDI!), For definiteness mp3. It is necessary to determine the sequence of chord changes, forming the harmony of the piece. By "music" we will mean typical European music - 12 semitones in an octave, harmony mainly based on major / minor triads, also reduced and increased triads and * sus2 / * sus4 are acceptable (chords with 2nd / 4th step instead of 3 th)
Some theory
Notes in European music are sounds with frequencies from a fixed set (more on this below), and sounds that differ in frequency of 2, 4, 8 ... are indicated by one note. Musical intervals are fixed frequency ratios of two notes. This interval system is organized as follows:
- the interval f1 / f2 == 2 is called an octave
- The octave is divided into 12 equal (in the "logarithmic" sense) minimum intervals, called small seconds or semitones. If notes n1 and n2 are small seconds, then their frequencies f1 and f2 are related as
f2 / f1 = 2 1/12 . Two small seconds make up a large second, three - a small third, four - a large third, seven - a fifth. The rest of the intervals we will not need.
The letter designations of the notes in the notation adopted in Russia are:
A - A, B - B-flat, H - B, C - C, D - D, E - M, F - F, G - Sal.
# (sharp) indicates an increase in frequency by 1/2 tones, b (flat) - a decrease by 1/2 tones. Per octave of 12 semitones, the notes are displayed as follows:
ABHCC # / Db DD # / Eb EFF # / Gb GG # / Ab
')
Octaves have tricky names and numbers, but we are not interested, it is enough to know that the frequency of the “la” note of the first octave is 440 Hz. The frequencies of the remaining notes are easy to calculate, based on what was written above.
A chord consists of several simultaneously sounding notes. At the same time, they can be extracted sequentially (arpeggio, it is “busting” in the jargon of yard guitarists), but since the sound does not calm down immediately, the notes have time to sound together for a while. In the European tradition, the most common chords of the three sounds (actually triad). Major and minor triads are commonly used. In major chords, the 1st (starting from the lowest) and 2nd notes form a large third, and the 2nd and 3rd ones form the minor third, while in the minor, the 1st and 2nd ones form the minor, 2nd and 3rd is great. The 1st and 3rd notes in both cases form a fifth. There are also reduced (two small third) and increased (two large third) triads, and in rock music, sustained-chords are quite common (I don’t know how they are in Russian) - sus2 with a 2 nd note for 1/2 tone lower than that of the minor and sus4 with a 2 nd note ½ tones higher than that of the major. The 3rd note in both versions of the sustained-chord forms the 1st ordinary fifth.
In a single piece of music, it is rarely when all 12 notes are used equally. As a rule, there is a “base” subset of 7 notes, and notes are taken mainly from it. Such a subset can be defined using a mask of 0 and 1, superimposed on a vector of 12 notes. If to exaggerate, such a subset is called a tonality, and the set of all possible cyclic shifts of a tonality mask is called a fret. In European music, two frets are mainly used:
- major with mask 1 0 1 0 1 1 0 1 0 1 0 1
- minor with mask 1 0 1 1 0 1 0 1 1 0 1 0
The chords used in a particular key are constructed, to the extent possible, from the notes of that key.
You may notice that the masks of major and minor differ to the accuracy of the shift. Accordingly, the chords, for example, in C major and the corresponding A minor, are used the same (it was we who so unobtrusively returned to our task).
The note “from which” the mask was applied was called tonic. The number of the note entering the key, starting with the tonic, is called the degree. When talking about the structure of a particular chord, the steps are counted from its 1st note (the so-called pitch).
Chords are traditionally denoted by the symbol of its pitch, to which a chord type suffix is assigned to the right without a space. For example, note A (A):
- A - major triad
- Am - minor triad
- A5 + - increased triad (he has another, official designation, but I often come across this)
- Am5- - diminished triad (again, there are other designations)
- Asus2 - sustained second stage
- Asus4 - sustained fourth stage
[Offtopic for those who studied in the "muzykalka"] I heard about the differences between the melodic and harmonic minor and about the problems of temperament (going back to the roots of the 12th degree) too. But, as it seems to me, in the framework of this article, the above simplified description of the subject area is sufficient.
Go to practice
So, we need:
- unpack mp3 into an array of numbers, which is a graph of sound amplitude versus time
- determine which notes sound at any given time
- determine which chords form these notes
I didn’t bother with the first task - I took a ready sox sound converter that supports both mp3 and “raw” formats, where the sound is stored just like a graph of the amplitude versus time. In * nix-systems, it is trivially set using the package manager - on Ubuntu it looks like this:
$ sudo apt-get install sox
$ sudo apt-get install lame
The second line puts the LAME mp3 encoder.
Under Windows, sox can be downloaded from the official site, but then you have to suffer a little with searching the Internet for suitable LAME DLLs.
With the second task, in principle, everything is simple. In order to understand which notes sound at a particular point in time, it is necessary to perform a spectral analysis of a piece of our array with amplitudes in the range of indices corresponding to a small neighborhood of this moment. As a result of spectral analysis, we obtain amplitudes for a variety of frequencies that "compose" the analyzed piece of sound. It is necessary to filter the frequencies, highlighting those of them that are close to the frequencies of the notes, and select the largest of them - they correspond to the loudest notes. I say “close,” not “equal,” because in nature there are no perfectly tuned musical instruments; This especially applies to guitars.
For spectral analysis of a discrete representation of a time-varying signal, you can use the window fast Fourier transform. I tore the simplest non-optimized FFT implementation from the Internet, translated it from C ++ to Scala, and took the Hanna function as a window function. More about this all can be read in the relevant articles of Wikipedia.
After receiving an array of amplitudes by frequency, we select frequencies in the vicinity (its default size is 1/4 semitones) around the frequency of each note in a certain octave range (experience shows that it is best to analyze octaves with a large second or third). In each such neighborhood, we calculate the maximum amplitude and consider it as the loudness of the corresponding note. After that, we summarize the “loudness” of each note by all octaves and, finally, we divide all the elements of the resulting array of 12 “loudnesses” by the value of its maximum element. The resulting vector of 12 elements in different sources is called a chromogram (chromagram).
Here it is impossible not to mention a pair of subtleties. Firstly, for different works the convenient range of octaves for analysis is different - for example, the introduction to My Friend Of Misery Metallics is played, apparently, on a bass guitar and sounds quite low; in the upper octaves, there are mostly overtones and left frequencies from the distortion, which only interfere.
Secondly, there are no perfectly tuned guitars in nature. This is probably due to the fact that the strings depending on the frets are differently extended during clamping (well, in general, the fingers put uneven pressure on them). In addition, this tool quickly gets upset in the process of playing on it. For example, in the acoustic recordings of Letov with the setting of the full finish - well, this can be understood. But why, in the same My Friend Of Misery, one not-remember-which note stably sounds exactly a quarter of a tone, not that higher, not that lower — a mystery. And even with well-tuned guitars on the records of all kinds of home-based artists, the line usually does not coincide with the canonical one in terms of total height — i.e. The “la” of the first octave may not be exactly 440 hertz.
In order to neutralize such shoals, it was necessary to envisage in the program the possibility of compensating for a general shift in the order. But with the frustration of individual strings and, in general, the indispensable “inconvenience” of guitars can not be helped. So ambush with the main rock instrument.
[Another Offtopic] The set of songs that will be mentioned in this, so to speak, “essay” may seem somewhat wild. However, the selection criteria were very simple:
- the piece must begin with the introduction “on some chords” (without a complex melody)
- it is desirable that the main instrument in the arrangement was a piano or, even better, electronic keys. If the arrangement is guitar, the recording should be studio (see above for the features of this wonderful instrument)
That is, I tried to simplify my life, at least at the beginning of torment with the selection of each song.
But back to our three tasks.
The remaining, third, task seems trivial - we select the three loudest notes and add a chord out of them. But in reality, this will not work (well, not quite anything - see below, but there is very little sense from this approach). And in general, this task was the most difficult of all.
Now about everything in order.
Naive chord determination method
At first, I did exactly as described above - after analyzing each “window” of the sound file I selected the three loudest notes and tried to make a chord out of them.
The first composition in which I tried to experience the magical effect of my miracle program was “Judas will be in paradise” by Letov in the variant from the Tyumen bootleg aka “Russian Field of Experiments (Acoustics)”. Vstulenie to this song is a dolbyob on a minor triad for about ten seconds.
However, having banished my program at the beginning of this song, I did not find a single (!) Chord Em in the output. Basically nothing was determined; occasionally any completely “left” nonsense climbed. What was the matter, it was not clear. I had to implement a private dump of each window in the form of a histogram of '*' symbols. From the histogram, first of all, it turned out that the structure of the guitar differs by about a quarter of a tone from nominal. OK, we introduce the amendment. Hooray! The notes E and H began to be determined - the 1st and 3rd in the chord. But where is G?
Further investigation of the dump revealed the following:
- The bass "mi" spectrum is smeared from D to F # with several local maxima, as a result, the second loudest note sometimes turns out to be D #
- From somewhere persistently climbs "la" (maybe this is a quint unterton from "mi"?). And when D # disappears somewhere, it takes its place. In this case, there is a chance to get in the output of Asus2, which is the same as Esus4, up to the choice of the bass note (in music this is called “appeal”). Already something, but I need Em!
- “Salt” in the chord Em in its standard fingering (in the first position) sounds only on one string - on the third (for comparison, “mi” - on three). And in this underground record, apparently, due to the poor quality of the equipment, most of the frequencies are severely cut.
Apparently, therefore, G rarely even turns out to be in 4th place.
In general, I scored on the selection of Letov. And in general, it became clear that we need to look for another way to analyze the chromogram. But, in fairness, I must say that there exists in nature at least one fragment, which is normally chosen in this way. This is an introduction to the song of Olga Pulatova “Pink Elephant”, which is an arpeggio on electronic keys. The program on it produced the following result (after manual cleaning of artifacts formed at the junctions of chords and removing consecutive repeats): Fm Cm (c db f) Ab Abm Eb Ebm B. ((c db f) - non-standard consonance, which without special damage may be replaced by Db). An independent check shows that the chords are correct.
Here it is, the power of a blunt piece of iron! With the hands of Olin delicacy with three tonalities for 8 chords, you can select a long and unsuccessfully ... But, alas, I repeat, this is the only composition I know that is successfully analyzed in this way. The reasons for the failure are understandable - on the one hand, the overtones and “left” frequencies of the guitar “lotions” interfere, on the other hand, the chords rarely sound by themselves, over them with higher, and the loudness usually includes the melody - vocals, guitar / keyboard solo and t .P. Melody rarely fits completely into harmony on notes - it is too sad, as a result, “temporary” harmonies are constantly formed in the stream of sound that do not correspond to any canonical chords, and everything breaks.
Slightly less naive way
I had to go to Google and dig. The topic turned out to be quite popular in the scientific and near-scientific environment, and in nature there is something to read about it, if you are not afraid of terms like hidden Markov model, naive bayesian classifier, gaussian mix, expectation maximization etc. At first I was afraid to climb into all this jungle. Then figured out on the sly.
Here is the article that turned out to be the most useful for me:
http://academia.edu/1026470/Enhancing_chord_classification_through_neighbourhood_histograms
To begin with, the authors propose not to look for exact matches with chords, but to evaluate the degree of “proximity” of the chromogram to the chord. They offer three ways to assess such proximity:
- maximal chromogram dot product per chord pattern
- naive bayes classifier
- estimating the parameters of a Gaussian mixture using the expectation maximization method and using the Mahalanobis distance as a measure of proximity of chromograms
After a few more detailed studies from other sources, I threw the third way out - he, judging by the conclusions from the above article, gives results a little better than the trivial first method, and hemorrhoids with matrix arithmetic, calculation of determinants, etc. lot.
But the first two I implemented.
The first way is super simple. Suppose we have a chord (for definiteness Am) and a chromogram. How to determine how the hromogram "similar" to the chord?
We take the mask of notes that sound in a chord - like the one we drew for the key. For Am, it will be 1 0 0 1 0 0 0 1 0 0 0 0. We multiply this mask as a scalar by the chromogram, as if they were 12-dimensional vectors (well, that is, we stupidly summarize the elements of the chromogram with those indices that are marked by one in the mask) . Voila - here it is, a measure of "similarity." We look through all the chords that we know, we find the one with the “similarity” the biggest - we believe that it sounds.
The second method is slightly more difficult to implement, but requires training data. It is based on the Bayes theorem. "On the fingers" it looks like this.
There is a concept of conditional probability: conditional probability P (A | B) is the probability of an event A , provided that event B has occurred. This value is determined by the following identity: P (AB) == P (A | B) * P (B) , where P (AB) is the probability of the joint occurrence of events A and B.
From here:
P (AB) == P (A | B) * P (B)
P (AB) == P (B | A) * P (A)
That is, under the condition of nonzero P (A)
P (B | A) == P (A | B) * P (B) / P (A)
This is the Bayes theorem.
How do we use it? Let us rewrite the formulation of the theorem in convenient notation for our problem:
P (Chord | Chroma) = P (Chroma | Chord) * P (Chord) / P (Chroma) ,
where Chord is a chord, Chroma is a chromogram
If we learn from somewhere the distribution of chromograms depending on the chord, then we can find the most plausible chord for a given chromogram, by maximizing the piece P (Chroma | Chord) * P (Chord) - since the chromogram is given, and P (Chroma) , so constant.
It remains to understand where to get the distribution of P (Chroma | Chord) . For example, you can let the program “listen” to the recordings of specific known chords so that it can estimate these distributions based on them. But there is a nuance. The probability of obtaining a specific value of a chromogram in the “training” examples is negligible - simply because there are very many possible values. As a result, when using learning results for real work in the overwhelming majority of cases, P (Chroma | Chord) will be zero for all Chord values, and there will be nothing to maximize.
It is possible (and necessary) before classification to simplify chromograms, for example, by dividing the range of relative amplitude [0, 1], on which the components of the chromogram are defined, say, 3 parts (with the meaning “almost as loud as the loudest note”, “several quieter than the loudest note "," very quiet compared to the loudest note "). But still there will be too many options.
The next thing you can do is to assume that the probability distribution of each component of the chromogram is independent of the other components. In this case, P (Chroma | Chord) = P (c 1 | Chord) * ... * P (c 12 | Chord) , where c 1 .. c 12 are components.
chromograms, and for this particular case we obtain the following formulation of the Bayes theorem:

But P (c i | Chord) can already be extracted even from a scant amount of training data - if, of course, the chromogram is “simplified” by limiting the definition of ci to three values, as we agreed above.
It remains to take P (Chord) from somewhere for all the chords in question. It does not matter - any collection of songs with chords will do for this, the main thing is that there are a lot of songs and they are different authors.
A classifier based on maximizing the expression P (c 1 | Chord) * ... * P (c 12 | Chord) * P (Chord) using the Chord parameter is called a naive Bayesian classifier. And in this particular case, its “naivety” is essential, since in reality the components of the chromogram are dependent random variables - for example, due to the same overtones. However, as we will see later, this approach works.
All this is easily realized - the code of the classifier itself and the “subsystem” of its training is far less than the description given here. I taught him on a set of major and minor piano chords from some free samples website and a compilation of an original song of the 90s with chords (the first thing that was found on the Internet as a single text file).
Now about the results of field trials. In the tests participated, in addition to the already mentioned My Friend Of Misery and “Pink Elephant”, the following compositions:
- Chizh & Co "Assol". Acoustic guitar, "tricky" chords, the first half of the song in a re-minor with not too strong missing in some places
- E.Letov "Soldiers are not born" in the version from the concert collection "Music of Spring". Acoustic guitar, seemingly normally tuned ... Chords - the usual triads, marcheshaped "battle", all in one key. The recording, albeit a concert, of good quality
- O. Pulatova "In a dream" from "Home Records". Acoustic piano, terrible recording quality; begins with the usual triad, perhaps with a modified bass, then melodic decorations begin. There are sounds for tonality at the hearing, but not very radical ... Although at the “Elephant” they are not very radical at the hearing ...
What happened. Both classifiers work very hard, all the while jumping from chord to chord. Naive Bayes are slightly more stable than the maximum of the scalar product, but it seems that only because it “knows” less chords (only major and minor). Since he, in contrast to the “scalar” brother, “knows” the probabilities with which different chords occur in the author’s damn song of the 90s, he behaves somewhat bydlovato, trying, roughly speaking, to shove the “three thugs” everywhere . Glimpses of reason are found in both classifiers, but for some reason, as a rule, on different fragments of the same work. Best of all, they coped with Misery. Bayes periodically fairly consistently gave out Dm and Am locomotives, which is correct (there is Dsus2 / E type harmony Am / E many, many times; / E is with bass "mi" in the sense). The “scalar” classifier who knows too many chords randomly wandered between Dsus2, Asus2 (aka Dsus4), D, Dm, D5 + and the left trash trying to recognize Dm, and behaved in the same way on Am.
Something managed to pull out of the "In a dream." Despite the poor sound quality, it was possible to manually identify the almost correct chords of the entry Cm Eb Bm (actually, the last chord B, as it should be in C minor) and the verse Cm Gm Cm Gm Ab F Ab F. The second, “decorated” part of the entry drowned in the garbage (looking ahead - I never picked it up, the more advanced classification methods also give out nonsense).
From “Soldiers Are Not Born,” they didn’t manage to get anything at all ... I don’t understand why. In the dump spectrum garbage. But it sounds normal to hear and pick up by hand is quite possible - Am CGH is there in the introduction, however, I’m not sure about tonality - the famous beast has arrived in the ear).
Naive Bayes coped better with “Assol”. He clearly liked the CSP-shnaya harmony in the d-minor, and glimpses of reason he happened quite often - he picked up the percentages of 20-25 chords correctly, which is against the general sad background and taking into account the “cunning” chords Comrade. Chigrakova not bad. But why did he replace almost all A on F # and F # m? Nonconformist, however.
In general, it was clear that we need to dig further.
We are in flight, and we have nothing to lose except chains. But not his, and Markov
Why do the above methods work so badly? If you know how to play something, imagine that you are offered to pick up a song, playing separately fragments in length of half a second, and not in order, but separately, so that you could not take into account the already selected part when working with the next “quantum”. Will you have something? I would venture to suggest that even if you have absolute hearing, the result will be deplorable.
Therefore, the authors of the above-mentioned work (as well as other similar studies) suggest using musical knowledge as they are expressed by evaluating the “similarity” of a chromogram to different chords. They have this secret knowledge that the probability of meeting one of the chords, which has already been encountered in the composition (or rather, in some of its time window), is higher than this probability for previously unseen chords. At the same time, they take into account the "fuzziness" of recognition of chords, the frequency of their occurrence in the analyzed window, etc.
In general, this is equivalent to such empirical knowledge "Songs are usually written in one, maximum two tonalities, and therefore the set of chords used in them is limited."
I decided to go a little different way. I proceeded from the following:
- Firstly, it should be noted that with a small size of the analyzed using the Fourier transform of the window, it is likely that the chord between two successively running windows does not change (several consecutive windows fall within the period of one chord)
- -, . , , «» (, G Gm, Am Dm, , G, B Dm — Gm). , .
With this assumption, you can use Markov chains to simulate the process of changing chords.
Imagine a system with a finite (or infinite but countable, i.e. "numbered") the set of states S . Let it “live” in discrete time, which has an initial “0th” moment and then each moment of time can be designated by its number - t 1 , t 2 , etc. Let given probability distribution for the initial state of the system P 0 (S i ) and transition probabilities P (S (t n ) = S i | S (t n-1 ) = S j ). Such a random process, when the probability of a system transitioning to a specific state depends only on its current state, is called a Markov chain (in our case, with discrete time). If the transition probability distribution does not depend on the time t n , the Markov chain is called homogeneous.
I nadergal distribution of the first chord and transitions from a heap of songs, unpacking 40-megabyte chm-nickname with the name like "all Russian rock with chords." However, the authors “drive” - there are no chords there even for some Cinema and Crematorium albums, not to mention such exotic as Pulatova (there are texts, interestingly, there are). Still, the array of collections is quite large, so we can assume that the sample is representative enough to estimate the parameters of our Markov chain. Analysis of the songs was from 10 pm to at least 5 am the next day, however, on the "atomic" netbook.
Go ahead.Remember the Bayes theorem - P (Chord | Chroma) = P (Chroma | Chord) * P (Chord) / P (Chroma) ? With the help of our Markov chain, we will evaluate P (Chord) , and P (Chroma | Chord), let it still be evaluated by naive Bayesian and "scalar" classifiers. Regarding the latter, we, in fact, don’t need a “real” probability, so we can consider our inner product for chromogram to chord mask as “probability” that this chromogram corresponds to this chord. Well, you can also normalize these scalar pieces so that their sum over all chords is equal to 1, although it is not necessary to search for the maximum, and I scored them.
So we can estimate P (Chord (t 0 ) = C i ), based on the statistical evaluation of the distribution of the first chords in the Russian rock compilation (in this way, we take into account the actually different frequency of using different tonalities). For the next windows, we can evaluate P (Chord (t n ) = C n ) as
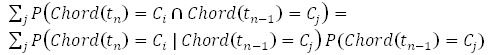
where P (Chord (t n-1 ) = C j ) were evaluated at the previous step. Find the maximum value of this expression for all i and get the most likely chord. Please note - here we take into account the fact that we do not know for sure what chord sounded in the previous window, we only have an estimate of the probability distribution of different chords.
As for the probability of “not moving” from chord to chord, I added the corresponding command line parameter and select the optimal value manually. In fact, this probability depends on the ratio between the duration of the stream window being analyzed and the musical tempo of the piece.
The above algorithm with proper selection of parameters proved to be very stable. Stumbling off the right path when trying to “bydolofikatsii” some difficult harmony, he honestly tries to return from the split ball, and most often he succeeds.
A couple of small optimizations
Optimization number 1. It was noted that the classifier "blows the roof", as a rule, on different fragments. It is also noted that if the same chord defined the classifier several times in a row, this chord is usually correct. These observations led to the following optimization: we start the ring buffer for several chords and push the chords there from the output of both classifiers. If once again the classifiers gave out different chords for the same window, take the one that occurs more often in the buffer (well, if it is equally common or not at all, then the first of the two).
Optimization №2.Different tonalities are used in music (especially guitar, where the fingering depends on them) with different frequencies. Basically, the people, of course, love those who have fewer alteration icons in the key — that is, in A minor / C major, E minor / G major, D minor / F major, or in the extreme case of B minor / D major.
Because of this, the statistics on transitions between chords for the most common keys are “better” than for less common ones. Hence the possibility of the possibility of “virtual transposition” —the command line keys that say the program “pick up chords in the tone that you see, but take the transition probabilities as if everything sounds n / half lower / higher”.
This approach is often used in manual selection - for example, we know that the song is in C minor, but we pick up chords in A minor, mumbling a melody a half tone lower, because what are the chords in this C minor? and the fingers keep the barre tired all the time.
The results of this stage are as follows: when applying the approach described above with both optimizations, we managed to find chords for the songs of O. Pulatova “In a dream” (except for the second part of the introduction) and “The river of times” (introduction and verse; tonality is a certain mixture of ly minor) with the accuracy of selection of about 70% or even slightly more. Hooray!
As for the second half of the introduction to "In a dream" - the best implementation, apparently, will be to go to Odessa, by chance there meet the author, ask her for chords, hardcore.
Viterbi Algorithm
The Viterbi algorithm allows using indirect data (well, that is, in our case, chromogram) for a certain period of the Markov chain’s life, to obtain the most likely sequence of states (chords) that the process has gone through during this period. The algorithm is very simple, and I tried to implement it, but, I see, I do not know how to prepare it. Depending on the likelihood of “not moving,” it either sticks on one chord, or gives out a bunch of garbage (though usually in the right tone). Perhaps this is due to the requirement that “the results of the observations should be 1-to-1 correspond to the“ steps ”of the random process passed.” But, on the other hand, who prevents us from believing that our “step” has a fixed physical lifetime, and then the next step comes, even if the state has not changed? I do not know.Or maybe just somewhere there are errors in the code - debugging such things is not easy ...
Well, that's all. Thanks for attention!
Sources can be taken here: https://github.com/t0mm/ChordDetector
Source: https://habr.com/ru/post/193514/
All Articles