Mathematical model Lego Segway
Good afternoon, dear colleagues. This article will be a continuation of the topic begun in the post habrahabr.ru/post/178103 .
We will continue from the moment when we already have the constructive constant values for the Lego engine, and we can proceed to the design and calculation of the robot. As a prototype will focus on the Segway. This is one of the most illustrative problems of the theory of automatic control. I present the construction of this mechanism.

To begin with, let's stop at the conclusion of the mathematical model of our robot. We select the generalized coordinates as follows:
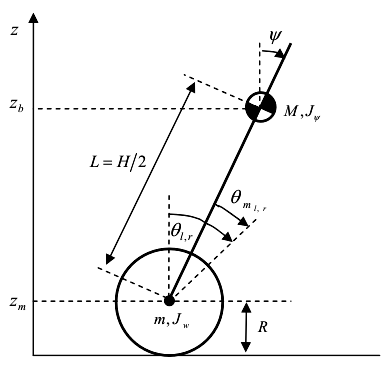
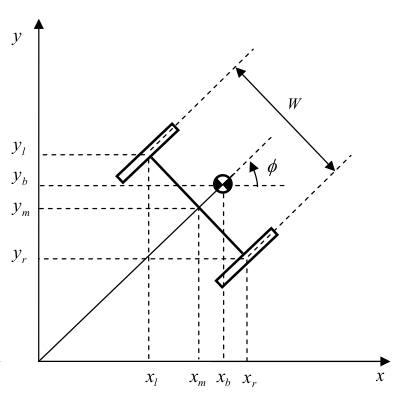
All designations of mass and moment of inertia are presented in the figure. It is assumed that our robot moves only in one plane XOZ. We will consider the Segway as an integral brick, without separately counting the moments of inertia of engines and wheels, to reduce the size of the equations of the system.
We write the equations of the coordinates of the center of mass of the system:
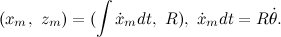

')
Now calmly write the equation for Lagrangian:
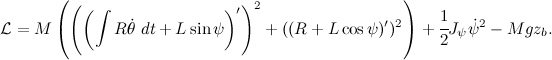
To automate the calculations, we use the Maxima symbolic computing system and its WxMaxima graphical environment. Enter the resulting expression in the command line:
The command \ verb | trigsimp | is used to simplify trigonometric expressions, and \ verb | expand | to expand the brackets. The command \ verb | tex | allows you to translate the result into tex-format, which will allow to display formulas in a tex-document or in the form of drawings.
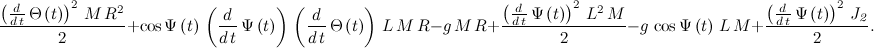
We write the derivatives in a compact form, we obtain the following equation:
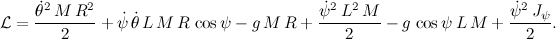
And we write the Lagrange equation as follows:
Program for Maxima:
By completing the specified actions we get:
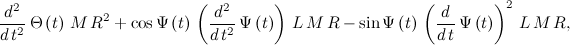
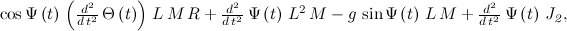
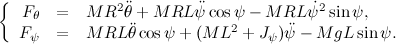
Next, we make equations for the engines of our Segway, using the material from the previous post habrahabr.ru/post/178103 :
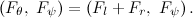
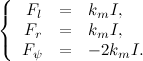
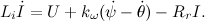
Since the inductance of the winding is extremely small, we set L = 0:

We get:

Now let's equate our moment equations, leaving only the elements with the control voltage on the left:
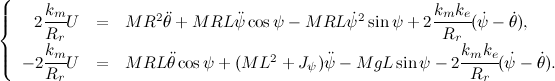
In order to use the equation and calculation of the matrix of feedback coefficients, linearize the resulting model. We use the first wonderful limit, we substitute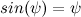 and
and 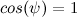 . We will also neglect the remaining nonlinearities:
. We will also neglect the remaining nonlinearities:

Now it is possible to write the received messages in a matrix form, having accepted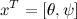 :
:
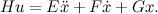
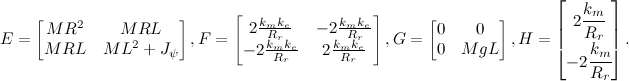
For us, this is an unusual form, so from these matrices we need to glue two matrices, the state matrix of our system and the control matrix. To do this, expand the state variable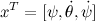 adding one more equation:
adding one more equation:
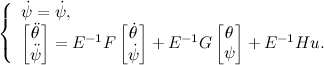

Now, we have obtained a third-order system and know all the dynamics and response to control actions. In order to make it sustainable, we must write the matrices describing the deliberately stable system. Use for this Newton's binomial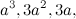 Where
Where  . Here
. Here 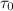 the table value of the transition time of the reference model,
the table value of the transition time of the reference model,  the transition time of our robot model, which we assumed was 0.3 seconds. Making a reference model, calculating its own numbers
the transition time of our robot model, which we assumed was 0.3 seconds. Making a reference model, calculating its own numbers 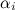 , Ackerman’s formula can be used to calculate feedback coefficients:
, Ackerman’s formula can be used to calculate feedback coefficients:
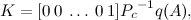
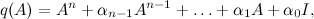
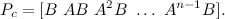
But not everything is as smooth as we would like. The obtained coefficients will most likely not be working, since we did not impose restrictions on the control voltage, although it is only 7 [V]. To fix this, it is necessary to model the system and reduce the coefficients for the angular velocities of the pendulum and the wheels of the robot.

The blue line for us will be the most suitable for the ratio of overshoot and transition time. After that we have a working program for the robot.
We will continue from the moment when we already have the constructive constant values for the Lego engine, and we can proceed to the design and calculation of the robot. As a prototype will focus on the Segway. This is one of the most illustrative problems of the theory of automatic control. I present the construction of this mechanism.

To begin with, let's stop at the conclusion of the mathematical model of our robot. We select the generalized coordinates as follows:


All designations of mass and moment of inertia are presented in the figure. It is assumed that our robot moves only in one plane XOZ. We will consider the Segway as an integral brick, without separately counting the moments of inertia of engines and wheels, to reduce the size of the equations of the system.
We write the equations of the coordinates of the center of mass of the system:
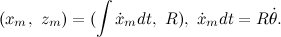

')
Now calmly write the equation for Lagrangian:
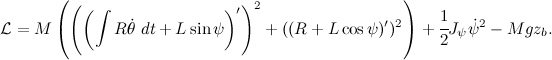
To automate the calculations, we use the Maxima symbolic computing system and its WxMaxima graphical environment. Enter the resulting expression in the command line:
V:expand( trigsimp( ((diff(integrate(R*diff(Theta(t),t),t)+L*sin(Psi(t)),t))^2+ (diff(R+L*cos(Psi(t)),t))^2)*M/2 +J2*(diff(Psi(t),t))^2/2-M*g*(R+L*cos(Psi(t))) ) ); tex(V); The command \ verb | trigsimp | is used to simplify trigonometric expressions, and \ verb | expand | to expand the brackets. The command \ verb | tex | allows you to translate the result into tex-format, which will allow to display formulas in a tex-document or in the form of drawings.
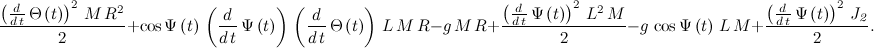
We write the derivatives in a compact form, we obtain the following equation:
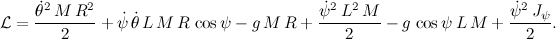
And we write the Lagrange equation as follows:
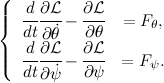
Program for Maxima:
U:expand(diff(diff(V,diff(Ttheta(t),t)),t)-diff(V,Theta(t))); Y:expand(diff(diff(V,diff(Psi(t),t)),t)-diff(V,Psi(t))); tex(U); tex(Y); By completing the specified actions we get:
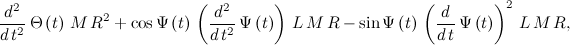
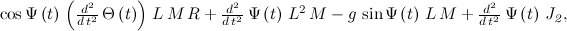
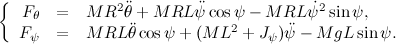
Next, we make equations for the engines of our Segway, using the material from the previous post habrahabr.ru/post/178103 :
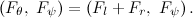
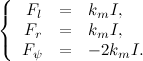
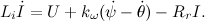
Since the inductance of the winding is extremely small, we set L = 0:

We get:

Now let's equate our moment equations, leaving only the elements with the control voltage on the left:
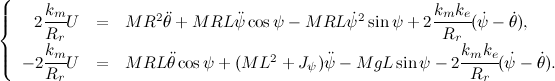
In order to use the equation and calculation of the matrix of feedback coefficients, linearize the resulting model. We use the first wonderful limit, we substitute
 and
and 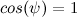 . We will also neglect the remaining nonlinearities:
. We will also neglect the remaining nonlinearities:
Now it is possible to write the received messages in a matrix form, having accepted
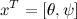 :
: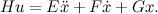
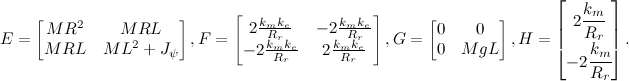
For us, this is an unusual form, so from these matrices we need to glue two matrices, the state matrix of our system and the control matrix. To do this, expand the state variable
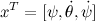 adding one more equation:
adding one more equation: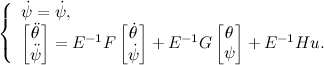

Now, we have obtained a third-order system and know all the dynamics and response to control actions. In order to make it sustainable, we must write the matrices describing the deliberately stable system. Use for this Newton's binomial
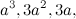 Where
Where  . Here
. Here 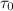 the table value of the transition time of the reference model,
the table value of the transition time of the reference model,  the transition time of our robot model, which we assumed was 0.3 seconds. Making a reference model, calculating its own numbers
the transition time of our robot model, which we assumed was 0.3 seconds. Making a reference model, calculating its own numbers 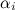 , Ackerman’s formula can be used to calculate feedback coefficients:
, Ackerman’s formula can be used to calculate feedback coefficients: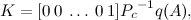
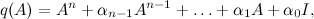
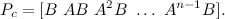
But not everything is as smooth as we would like. The obtained coefficients will most likely not be working, since we did not impose restrictions on the control voltage, although it is only 7 [V]. To fix this, it is necessary to model the system and reduce the coefficients for the angular velocities of the pendulum and the wheels of the robot.

The blue line for us will be the most suitable for the ratio of overshoot and transition time. After that we have a working program for the robot.
#define GYRO_PORT IN_1 #define LEFT_MOTOR OUT_C #define RIGHT_MOTOR OUT_B #define BOTH_MOTORS OUT_BC #define WAIT_TIME 8.0 #define KGYROANGLE 0.487 #define KSPEED 0.024 #define KGYROSPEED 0.153 #define KPOS 0 task main(){ float time = WAIT_TIME * 0.001; float segway_angle = 0; float segway_speed; float wheel_angle = 0, last_wheel_angle; float wheel_speed; float max_voltage; int u; SetSensorHTGyro(GYRO_PORT); Wait(50); while(true) { max_voltage = BatteryLevel() / 1000; segway_speed = (SensorHTGyro(GYRO_PORT) + 2); segway_angle += segway_speed * time; last_wheel_angle = wheel_angle; wheel_angle = (MotorRotationCount(LEFT_MOTOR) + MotorRotationCount(RIGHT_MOTOR)) / 2; wheel_speed = (wheel_angle - last_wheel_angle) / time; u = KGYROANGLE * segway_angle + KSPEED * wheel_speed + KGYROSPEED * segway_speed + KPOS * wheel_angle; u = u * 100 / max_voltage; if (abs(u) > 100){ u = sign(u) * 100; } OnFwd(BOTH_MOTORS, u); Wait(WAIT_TIME); } } Source: https://habr.com/ru/post/193272/
All Articles