Scilab - from factorial search to tic-tac-toe
Good evening, friends, today is Friday and I, by tradition, would like to share with you my research.
Funny situation. Those few programmers (people associated with programming), whom I know personally, have never written games, and people who are far from the concept of “professional programmer” just like a polar bear from the principles of humanism, no no, they will bungle some uncanny unplayable under the tree.
One of the above named people is I.
In this article I want to kill two birds with one stone to tell people a little about the Scilab software package , and at the same time demonstrate its functions in an unusual way.
Today I will tell you about how I made tic tac toe in Scilab . For the details of mercy I ask for cat.

Thank you for the picture DrZugrik
')
Let's start with the fact that I am not a programmer, not a programmer at all, a very very not a programmer.
That is why I propose not to accept this article as a guide to action. This post I write only “just for fun” and in part to popularize Scilab.
The source file of the script is posted on GitHub , so if someone has a desire to improve the code, then I’m all for it.
So for a start, a brief help. What is Scilab?
A detailed answer to this question can be found on Wikipedia or on the official community website.
If you tell in your own words, Scilab, this discovery is an analogue of Matlab. With a very similar syntax, with similar procedures (many Matlab procedures have their own counterpart in Scilab), the interface of the most recent Scilab 5.4.1, with something vaguely reminiscent of Matlab five years ago, now it is quite comfortable to work with. Well and most importantly, Scilab has similar capabilities, certainly smaller than those of a commercial giant, but still quite sufficient for a student, novice scientist or just a curious engineer. Scilab has its own analog Simulink (although it is clearly inferior), you can also connect various modules, for example Maxima for symbolic computing (I didn’t work very reliably, but it worked). What is not a replacement for pirated copies of Matlab, established in colleges and universities?
An example of a package of applied mathematical programs can be seen in the screenshots under the spoiler.
Certainly learn Scilab, it may be a little more difficult. It is less debugged, there are bugs, and there are certainly fewer methods for working with it than with a big brother, but from time to time more and more answers to potential questions can be found on the Internet and in the program manuals.
Guides we are now the way and stocked. For writing tic tac toes, I needed the SCILAB package manual .
Creating graphic applications in the Scilab environment,
Well, Scilab's solution to engineering and math problems still does not hurt
What was the challenge.
Using the ability to create graphical interfaces in Scilab, write simple little tic tac toe for playing with a computer.
The source code (posted on GitHub ) is presented under the spoiler.
If to briefly describe it, a graphic window is first created, it houses 9 buttons of the playing field, a text label and a restart button. When you click on the button on the playing field, the game begins. Artificial intelligence, purely from the ceiling takes a value from 1 to 9 and if it freely “walks” there, if there is no further digging. At the end of each click handler, the check for the fulfillment of the victory condition is called (the cells of the field are represented as a matrix and we scoff at it in every way)
It looks something like this:
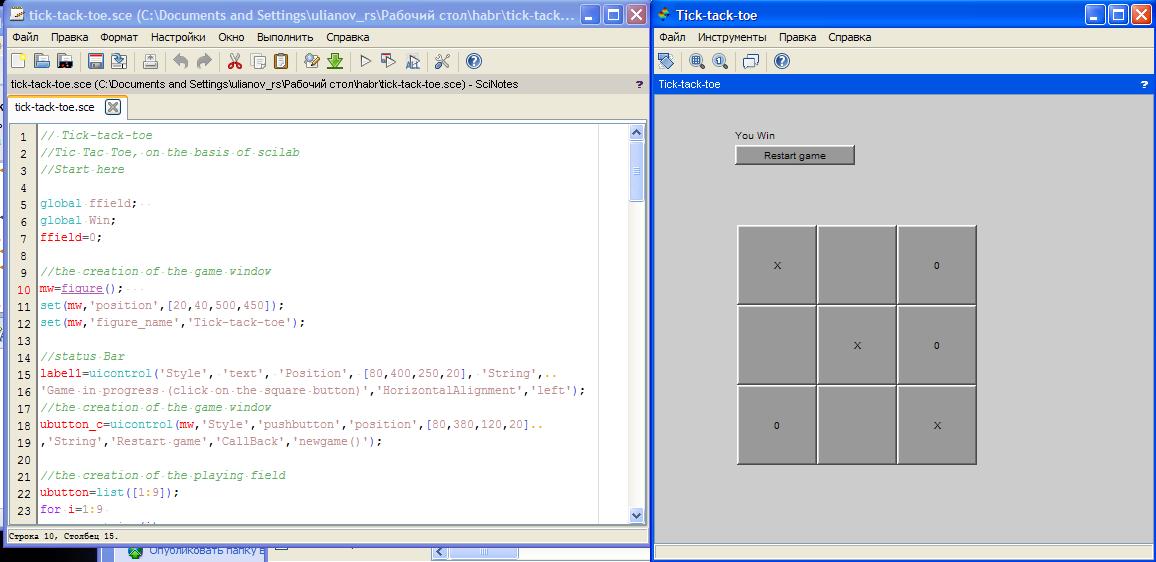
The code is certainly bad, but I hope that I can motivate someone to study this absolutely useful mathematical tool.
Have a good Friday and have a great weekend :)
Funny situation. Those few programmers (people associated with programming), whom I know personally, have never written games, and people who are far from the concept of “professional programmer” just like a polar bear from the principles of humanism, no no, they will bungle some uncanny unplayable under the tree.
One of the above named people is I.
In this article I want to kill two birds with one stone to tell people a little about the Scilab software package , and at the same time demonstrate its functions in an unusual way.
Today I will tell you about how I made tic tac toe in Scilab . For the details of mercy I ask for cat.

Thank you for the picture DrZugrik
')
Let's start with the fact that I am not a programmer, not a programmer at all, a very very not a programmer.
That is why I propose not to accept this article as a guide to action. This post I write only “just for fun” and in part to popularize Scilab.
The source file of the script is posted on GitHub , so if someone has a desire to improve the code, then I’m all for it.
So for a start, a brief help. What is Scilab?
A detailed answer to this question can be found on Wikipedia or on the official community website.
If you tell in your own words, Scilab, this discovery is an analogue of Matlab. With a very similar syntax, with similar procedures (many Matlab procedures have their own counterpart in Scilab), the interface of the most recent Scilab 5.4.1, with something vaguely reminiscent of Matlab five years ago, now it is quite comfortable to work with. Well and most importantly, Scilab has similar capabilities, certainly smaller than those of a commercial giant, but still quite sufficient for a student, novice scientist or just a curious engineer. Scilab has its own analog Simulink (although it is clearly inferior), you can also connect various modules, for example Maxima for symbolic computing (I didn’t work very reliably, but it worked). What is not a replacement for pirated copies of Matlab, established in colleges and universities?
An example of a package of applied mathematical programs can be seen in the screenshots under the spoiler.
Interface, graphics and factorials
graphics in Scilab
example of a function - finding factorial

graphics in Scilab

example of a function - finding factorial
Certainly learn Scilab, it may be a little more difficult. It is less debugged, there are bugs, and there are certainly fewer methods for working with it than with a big brother, but from time to time more and more answers to potential questions can be found on the Internet and in the program manuals.
Guides we are now the way and stocked. For writing tic tac toes, I needed the SCILAB package manual .
Creating graphic applications in the Scilab environment,
Well, Scilab's solution to engineering and math problems still does not hurt
What was the challenge.
Using the ability to create graphical interfaces in Scilab, write simple little tic tac toe for playing with a computer.
The source code (posted on GitHub ) is presented under the spoiler.
If to briefly describe it, a graphic window is first created, it houses 9 buttons of the playing field, a text label and a restart button. When you click on the button on the playing field, the game begins. Artificial intelligence, purely from the ceiling takes a value from 1 to 9 and if it freely “walks” there, if there is no further digging. At the end of each click handler, the check for the fulfillment of the victory condition is called (the cells of the field are represented as a matrix and we scoff at it in every way)
It looks something like this:
Source
// Tick-tack-toe //Tic Tac Toe, on the basis of scilab //Start here global ffield; global Win; ffield=0; //the creation of the game window mw=figure(); set(mw,'position',[20,40,500,450]); set(mw,'figure_name','Tick-tack-toe'); //status Bar label1=uicontrol('Style', 'text', 'Position', [80,400,250,20], 'String',.. 'Game in progress (click on the square button)','HorizontalAlignment','left'); //the creation of the restart button ubutton_c=uicontrol(mw,'Style','pushbutton','position',[80,380,120,20].. ,'String','Restart game','CallBack','newgame()'); //the creation of the playing field ubutton=list([1:9]); for i=1:9 num=string(i) y=ceil(i/3); x=i-((y-1)*3); ubutton(i)=uicontrol(mw,'Style','pushbutton','position',[80*x+2,80*y,80,80].. ,'String',' ','CallBack','press_button('+num+')'); end function y=press_button(button_num) //gaming activities global ffield; global Win; // Human Button_Value=get(ubutton(button_num),'String'); if Button_Value==" " then set(ubutton(button_num),'String',"X"); ffield=ffield+1; end // AI if ffield<9 then ct=comp_turn(); //get random action of AI buf=get(ubutton(ct),'String'); while buf ~= " " do ct=comp_turn(); //get random action of AI buf=get(ubutton(ct),'String'); end set(ubutton(ct),'String',"0"); // Ai chooses cell end ffield=ffield+1; //counter filled cells Winner() //find game winner endfunction function R=comp_turn() // Computer opponent action (random action) R = grand(1,1,"poi",4); if R>9 then R=9; end; if R<1 then R=1; end; endfunction function Winner() //find game winner function res=0; pw=0; cw=0; plfield=hypermat([3,3]); // results matrix for human cmfield=hypermat([3,3]); // results matrix for AI // check game field for ck=1:9 Button_Value=get(ubutton(ck),'String'); j=ceil(ck/3); i=ck-((j-1)*3); if Button_Value=="X" then plfield(j,i)=1; end if Button_Value=="0" then cmfield(j,i)=1; end end // check human results pb=pob_diag(plfield,3) ;//processing second diag. sm=prod(plfield,1)+prod(plfield,2)';//processing matrix if sum(sm)==1 then res=1; end; //check winning the hor. and vert. field if diag(plfield,0)==1 then res=1; end; //check winning field main diag. if pb==1 then res=1; end; //check winning field second diag. // check AI results pb=pob_diag(cmfield,3) //processing second diag. sm=prod(cmfield,1)+prod(cmfield,2)';//processing matrix if sum(sm)==1 then res=2; end; // check winning the hor. and vert. field if diag(cmfield,0)==1 then res=2; end; //check winning field main diag. if pb==1 then res=2; end; //check winning field second diag. // Deciding the winner if res==1 then set(label1,'String',"You Win"); end if res==2 then set(label1,'String',"Computer Win"); end if (ffield>=9) & (res==0) then set(label1,'String',"No Winner"); end endfunction function mult=pob_diag(A,N) // analysis of the secondary diagonal matrix mult=1; for i=1:N mult=mult*A(i,N+1-i); end endfunction function mult=find_one(Win) // analysis of the columns of the matrix mult=1; prod(Win,1)+prod(Win,2)' for i=1:2 mult=mult+i; end endfunction function newgame() // restart game (reset values) global ffield; global Win; global res; for i=1:9 y=ceil(i/3); x=i-((y-1)*3); set(ubutton(i),'String',' '); end; ffield=0; res=0 Win=0; set(label1, 'String','Game in progress (click on the square button)'); endfunction 
The code is certainly bad, but I hope that I can motivate someone to study this absolutely useful mathematical tool.
Have a good Friday and have a great weekend :)
Source: https://habr.com/ru/post/192834/
All Articles