Calculation of the intersection area of the circles by the Monte Carlo method
This article was born as a logical continuation of the Friday post about the Bootstrap method , and especially comments on it. Without defending the Bootstrap method, you should pay attention to the Monte Carlo methods. Here I want to share my experience of using Monte Carlo in one of my practical tasks, and also the rationale for the legitimacy of this application.
So, my task was to calculate the area of a figure, which is the intersection of circles, with the subsequent implementation in JavaScript. The area under the graph is an integral. Monte-Carlo integration is widely known, but, as many will rightly note, its application requires some justification. For details, I ask under the cat.
Justification
The task of calculating the area of intersection of two circles is a trivial geometric problem (the coordinates of the centers of the circles and their radii are known to us). The area of intersection of two circles is the sum of the areas of the corresponding segments of these circles. There are solutions for calculating the area of intersection of two, three, four circles in various particular cases.
')
But the solutions of the general case for the intersection of even three circles are far from being so trivial. In the process of searching, I found even studies on the calculation of the area of intersection of N circles , but they are as interesting as they are complex.
This is where the Monte-Carlo method comes into play. Thanks to modern computer power, this method allows a large number of statistical tests to be conducted, based on the results of which a generalization is made.
So, the algorithm for calculating the area of any shape by the Monte Carlo method is as follows:
- The figure fits into a rectangle. The coordinates of the sides of the rectangle are known, which means that its area is known.
- In a pseudo-random manner, a large number of points are generated inside the rectangle. For each point, it is determined whether the point fell inside the original shape or not.
- As a result, the area of the original figure is calculated from the usual proportion: the ratio of the number of points in the figure to the total number of generated points is equal to the ratio of the area of the figure to the area of the rectangle bounding it.
The last problem to be solved is that in some way it is necessary to determine whether a point has fallen inside the original shape. In my case, this problem is solved quite simply, since my figure consists of circles, the coordinates of the centers and the radii of which are known.
JavaScript task implementation
Drawing circles was done using the wonderful D3.js library . The algorithm of the initial mutual arrangement of circles is beyond the scope of this article, so we take the initial arrangement as a given.
We collect an array of intersections of pairs of circles
var nodes = d3.selectAll("circle.node"); var squares = []; var intersections = []; nodes.each(function(node){ // var r = this.r.baseVal.value; var s = 3.14159*r*r; squares.push({node: node, square: s, r: r}); // nodes.each(function(node2){ // var center_dist = Math.sqrt(Math.pow(node.x-node2.x, 2)+(Math.pow(node.y-node2.y, 2))); var radius_sum = r + this.r.baseVal.value; if(center_dist <= radius_sum && node.index != node2.index){ // . , node.r = r; node2.r = this.r.baseVal.value; if(isNewIntersection(intersections, node, node2)) intersections.push({node1: node, node2: node2, center_dist: center_dist}); } }); }); Consider the area of the figure
var areaCalculator = { intersections: [], // , frame: {}, // circles: [], // figureArea: 0, // monteCarlo: function(p){ // var circles = []; var x1_, y1_, x2_, y2_; // var inCirclesArr = function(node){ for(var j=0; j<circles.length; j++){ if(circles[j].index==node.index){ return true; } } return false; }; for(var i=0; i<this.intersections.length; i++){ if(!inCirclesArr(this.intersections[i].node1)){ circles.push(this.intersections[i].node1); } if(!inCirclesArr(this.intersections[i].node2)){ circles.push(this.intersections[i].node2); } } this.circles = circles; circles.sort(function(a,b){ return ax-ar > bx-br ? 1 : -1; }); x1_ = circles[0].x-circles[0].r; circles.sort(function(a,b){ return a.x+ar < b.x+br ? 1 : -1; }); x2_ = circles[0].x+circles[0].r; circles.sort(function(a,b){ return ay-ar > by-br ? 1 : -1; }); y1_ = circles[0].y-circles[0].r; circles.sort(function(a,b){ return a.y+ar < b.y+br ? 1 : -1; }); y2_ = circles[0].y+circles[0].r; this.frame.x1 = x1_; this.frame.x2 = x2_; this.frame.y1 = y1_; this.frame.y2 = y2_; this.frame.area = (x2_-x1_)*(y2_-y1_); // paintRect(this.frame); // p - . 100.000, var p_positive = 0; // // p for(var i=0; i<p; i++){ var x_rand = Math.random()*(x2_-x1_)+x1_; var y_rand = Math.random()*(y2_-y1_)+y1_; var yes = false; for(var j=0; j<circles.length; j++) { if(!yes && ( (circles[j].x-circles[j].r) <= x_rand && (circles[j].x+circles[j].r) >= x_rand && (circles[j].y-circles[j].r) <= y_rand && (circles[j].y+circles[j].r) >= y_rand ) ){ yes = true; p_positive++; } } } // = *- / - this.figureArea = this.frame.area*p_positive/p; } };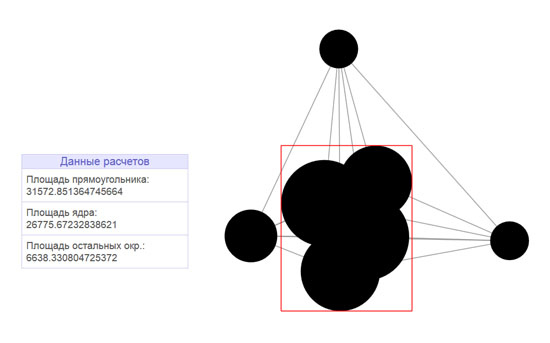
A pair of nails in the bootstrap method
If we speak about the Bootstrap method, then my personal opinion is that the random generation of a data set on an existing set in the general case cannot serve to evaluate patterns, since the generated information is not reliable. In general, this is only the words that are cleverer (and often more sharp), and many authors say, for example, Orlov in his Econometrics textbook .
Conclusion
Monte Carlo methods are quite viable and very useful in some cases, such as in mine. The capabilities of modern computers, even ordinary desktop machines, make it possible to operate with similar statistical methods with a sufficiently large number of tests and, accordingly, to obtain sufficient accuracy of the result. But with all this, of course, they are only a simplification of the model and can not claim to be something more.
Source: https://habr.com/ru/post/192272/
All Articles