Sudoku generation algorithm

Good day!
I think the Sudoku puzzle needs no introduction. Many of us spend a lot of time trying to solve it. For example, when you need to kill time on the road or just turn the brain so as not to dry. On Habré there are quite a few posts about solving a puzzle. But when a person solves a dozen, or maybe a hundred puzzles, then there will be an inquiring mind that will ask itself the question “But how does the Sudoku table come up with the only solution? And how can one describe the algorithm for a 9x9 grid? ”.
The above algorithm is quite logical. But my task was the description and implementation. All this is written under the cut.
')
Basic Sudoku Rules

- The number can appear only once in each line.
- A digit may appear only once in each bar.
- The figure can appear only once in each district (Area - a smaller square with a side of 3x3, in the image below highlighted in purple)

Step 1. Base the base mesh.
The grid must obey the rules of Sudoku. We place in the first line 1 2 ... 8 9, in the lines below we shift 3 positions to the left, i.e. 4 5 ... 2 3 and 7 8 ... 5 6.
Next, moving to the next area vertically we shift the previous area by 1 position to the left.
As a result, this grid should turn out; I will call it the basic one :

To implement create a class grid. Fill it in accordance with Step 1, in which table is a list of table values, the show method is just a visual output of the table.
class grid: def __init__(self,n = 3): """Generation of the base table""" self.n = n self.table = [[((i*n + i/n + j) % (n*n) + 1) for j in range(n*n)] for i in range(n*n)] print "The base table is ready!" def __del__(self): pass def show(self): for i in range(self.n*self.n): print self.table[i] Step 2. Shuffle the mesh
There are several types of permutations, after which the Sudoku table will remain in a valid state.
These include:
- Transpose the entire table — columns become rows and vice versa ( transposing )

- Exchange two strings within the same district ( swap_rows_small )
- Exchange of two columns within the same region ( swap_colums_small )
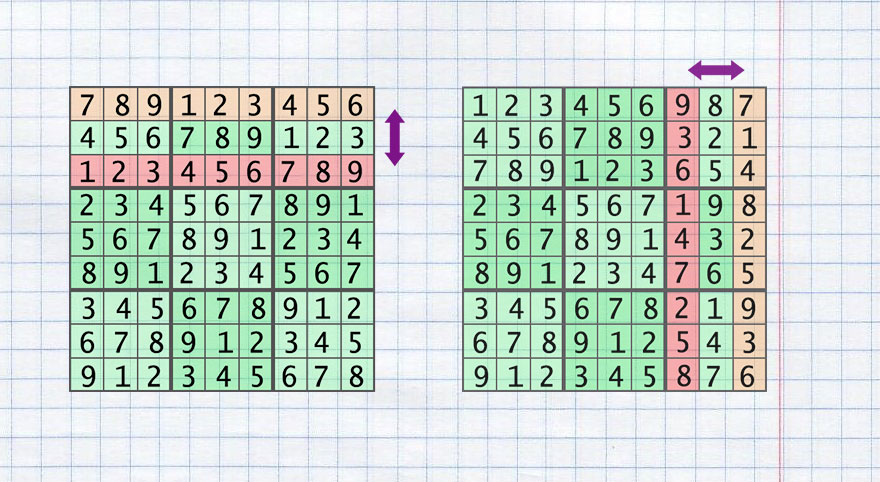
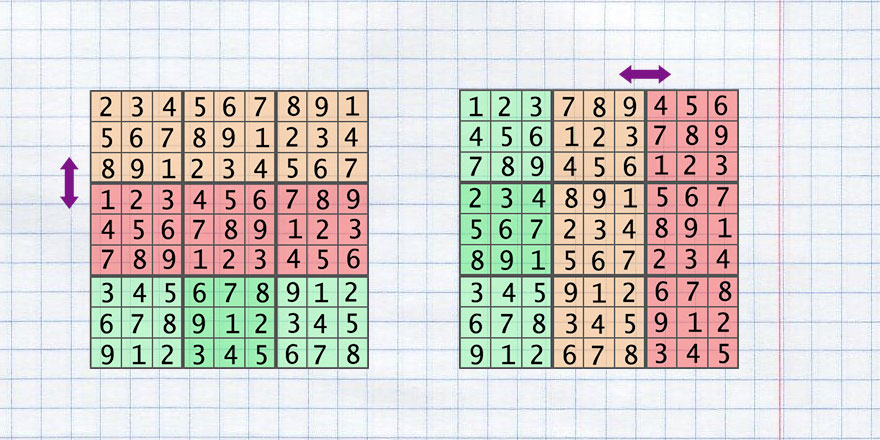
- Exchange of two areas horizontally ( swap_rows_area )
- Exchange of two areas vertically ( swap_colums_area )
For each of the permutations, we write a method:
transposing
def transposing(self): """ Transposing the whole grid """ self.table = map(list, zip(*self.table)) swap_rows_small
def swap_rows_small(self): """ Swap the two rows """ area = random.randrange(0,self.n,1) line1 = random.randrange(0,self.n,1) # N1 = area*self.n + line1 # 1 line2 = random.randrange(0,self.n,1) while (line1 == line2): line2 = random.randrange(0,self.n,1) N2 = area*self.n + line2 # 2 self.table[N1],self.table[N2] = self.table[N2], self.table[N1] swap_colums_small
For the exchange of columns, you can change the rows of the transposed table:
def swap_colums_small(self): grid.transposing(self) grid.swap_rows_small(self) grid.transposing(self) swap_rows_area
def swap_rows_area(self): """ Swap the two area horizon """ area1 = random.randrange(0,self.n,1) # area2 = random.randrange(0,self.n,1) while (area1 == area2): area2 = random.randrange(0,self.n,1) for i in range(0, self.n): N1, N2 = area1*self.n + i, area2*self.n + i self.table[N1], self.table[N2] = self.table[N2], self.table[N1] swap_colums_area
def swap_colums_small(self): grid.transposing(self) grid.swap_rows_area(self) grid.transposing(self) Maybe there are even more complex transformations, but I think we can limit ourselves to these. This framework is invariant to its structure, such permutations are almost the same as actions on matrices with respect to the determinant or rotation of the Rubik's Cube.
Now, in order to get a random combination, it is enough to run in a random order the functions of mixing. So do, amt - the number of mixing:
def mix(self,amt = 10): mix_func = ['self.transposing()', 'self.swap_rows_small()', 'self.swap_colums_small()', 'self.swap_rows_area()', 'self.swap_colums_area()'] for i in xrange(1, amt): id_func = random.randrange(0,len(mix_func),1) eval(mix_func[id_func]) Example 10 mixing iterations
base [1, 2, 3, 4, 5, 6, 7, 8, 9] [4, 5, 6, 7, 8, 9, 1, 2, 3] [7, 8, 9, 1, 2, 3, 4, 5, 6] [2, 3, 4, 5, 6, 7, 8, 9, 1] [5, 6, 7, 8, 9, 1, 2, 3, 4] [8, 9, 1, 2, 3, 4, 5, 6, 7] [3, 4, 5, 6, 7, 8, 9, 1, 2] [6, 7, 8, 9, 1, 2, 3, 4, 5] [9, 1, 2, 3, 4, 5, 6, 7, 8] swap_colums_area [7, 8, 9, 4, 5, 6, 1, 2, 3] [1, 2, 3, 7, 8, 9, 4, 5, 6] [4, 5, 6, 1, 2, 3, 7, 8, 9] [8, 9, 1, 5, 6, 7, 2, 3, 4] [2, 3, 4, 8, 9, 1, 5, 6, 7] [5, 6, 7, 2, 3, 4, 8, 9, 1] [9, 1, 2, 6, 7, 8, 3, 4, 5] [3, 4, 5, 9, 1, 2, 6, 7, 8] [6, 7, 8, 3, 4, 5, 9, 1, 2] swap_colums_small [7, 8, 9, 4, 5, 6, 2, 1, 3] [1, 2, 3, 7, 8, 9, 5, 4, 6] [4, 5, 6, 1, 2, 3, 8, 7, 9] [8, 9, 1, 5, 6, 7, 3, 2, 4] [2, 3, 4, 8, 9, 1, 6, 5, 7] [5, 6, 7, 2, 3, 4, 9, 8, 1] [9, 1, 2, 6, 7, 8, 4, 3, 5] [3, 4, 5, 9, 1, 2, 7, 6, 8] [6, 7, 8, 3, 4, 5, 1, 9, 2] swap_colums_small [7, 8, 9, 4, 5, 6, 1, 2, 3] [1, 2, 3, 7, 8, 9, 4, 5, 6] [4, 5, 6, 1, 2, 3, 7, 8, 9] [8, 9, 1, 5, 6, 7, 2, 3, 4] [2, 3, 4, 8, 9, 1, 5, 6, 7] [5, 6, 7, 2, 3, 4, 8, 9, 1] [9, 1, 2, 6, 7, 8, 3, 4, 5] [3, 4, 5, 9, 1, 2, 6, 7, 8] [6, 7, 8, 3, 4, 5, 9, 1, 2] transposing [7, 1, 4, 8, 2, 5, 9, 3, 6] [8, 2, 5, 9, 3, 6, 1, 4, 7] [9, 3, 6, 1, 4, 7, 2, 5, 8] [4, 7, 1, 5, 8, 2, 6, 9, 3] [5, 8, 2, 6, 9, 3, 7, 1, 4] [6, 9, 3, 7, 1, 4, 8, 2, 5] [1, 4, 7, 2, 5, 8, 3, 6, 9] [2, 5, 8, 3, 6, 9, 4, 7, 1] [3, 6, 9, 4, 7, 1, 5, 8, 2] swap_colums_small [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [4, 7, 1, 5, 8, 2, 3, 9, 6] [5, 8, 2, 6, 9, 3, 4, 1, 7] [6, 9, 3, 7, 1, 4, 5, 2, 8] [1, 4, 7, 2, 5, 8, 9, 6, 3] [2, 5, 8, 3, 6, 9, 1, 7, 4] [3, 6, 9, 4, 7, 1, 2, 8, 5] swap_rows_small [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [5, 8, 2, 6, 9, 3, 4, 1, 7] [4, 7, 1, 5, 8, 2, 3, 9, 6] [6, 9, 3, 7, 1, 4, 5, 2, 8] [1, 4, 7, 2, 5, 8, 9, 6, 3] [2, 5, 8, 3, 6, 9, 1, 7, 4] [3, 6, 9, 4, 7, 1, 2, 8, 5] swap_rows_small [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [5, 8, 2, 6, 9, 3, 4, 1, 7] [4, 7, 1, 5, 8, 2, 3, 9, 6] [6, 9, 3, 7, 1, 4, 5, 2, 8] [2, 5, 8, 3, 6, 9, 1, 7, 4] [1, 4, 7, 2, 5, 8, 9, 6, 3] [3, 6, 9, 4, 7, 1, 2, 8, 5] swap_rows_area [7, 1, 4, 8, 2, 5, 6, 3, 9] [8, 2, 5, 9, 3, 6, 7, 4, 1] [9, 3, 6, 1, 4, 7, 8, 5, 2] [2, 5, 8, 3, 6, 9, 1, 7, 4] [1, 4, 7, 2, 5, 8, 9, 6, 3] [3, 6, 9, 4, 7, 1, 2, 8, 5] [5, 8, 2, 6, 9, 3, 4, 1, 7] [4, 7, 1, 5, 8, 2, 3, 9, 6] [6, 9, 3, 7, 1, 4, 5, 2, 8] swap_colums_small [7, 1, 4, 8, 2, 5, 6, 9, 3] [8, 2, 5, 9, 3, 6, 7, 1, 4] [9, 3, 6, 1, 4, 7, 8, 2, 5] [2, 5, 8, 3, 6, 9, 1, 4, 7] [1, 4, 7, 2, 5, 8, 9, 3, 6] [3, 6, 9, 4, 7, 1, 2, 5, 8] [5, 8, 2, 6, 9, 3, 4, 7, 1] [4, 7, 1, 5, 8, 2, 3, 6, 9] [6, 9, 3, 7, 1, 4, 5, 8, 2] Step 3. Cell removal
After the obtained solution, we need to get the problem (it is in this sequence that we can guarantee the uniqueness of the solution). And this is the hardest part. How many can be removed to ensure the uniqueness of the decision? This is one of the important factors on which Sudoku difficulty depends. In total, there are 81 cells in Sudoku, usually considered easy when there are 30-35 “tips” on the field, 25-30 in the middle, and 20-25 in the complex. This data is a large set of real-world examples. There are no laws for complexity. You can make a 30-cell insoluble variant and a 22-cell “easy” one.
- Random approach - you can try to throw 50-60 cells at random, but where is the likelihood that Sudoku can be solved? For example, if 3 lines are filled (= 27 cells)
- Randomly with a simple constraint — for example, you can take some number N as a limit, so that N rows and columns can be empty. Taking N = 0 - for light levels, N = 1 - medium, N = 2 - difficult
So, let's proceed to the deletion of the cells (all options are equivalent, so we have 81 cells, which can be crossed out, so we will check everything by brute force):
- Select a random cell N
- Mark N Viewed
- Remove N
- Calculate solutions. If it is not the only one, then return N
The output will be the most difficult of the possible Sudoku options for this mixing. The variable variable evaluates complexity - the number of remaining elements.
flook = [[0 for j in range(example.n*example.n)] for i in range(example.n*example.n)] iterator = 0 difficult = example.n ** 4 # while iterator < example.n ** 4: i,j = random.randrange(0, example.n*example.n ,1), random.randrange(0, example.n*example.n ,1) # if flook[i][j] == 0: # iterator += 1 flook[i][j] = 1 # temp = example.table[i][j] # example.table[i][j] = 0 difficult -= 1 #, table_solution = [] for copy_i in range(0, example.n*example.n): table_solution.append(example.table[copy_i][:]) # i_solution = 0 for solution in solver.solve_sudoku((example.n, example.n), table_solution): i_solution += 1 # if i_solution != 1: # -- example.table[i][j] = temp difficult += 1 # example.show() print "difficult = ",difficult sudoku_generator.py
# coding=utf-8 import random import solver class grid: def __init__(self,n = 3): """ Generation of the base table """ self.n = n self.table = [[ ((i*n + i/n + j) % (n*n) + 1) for j in range(n*n)] for i in range(n*n)] print "The base table is ready!" def __del__(self): pass def show(self): for i in range(self.n*self.n): print self.table[i] def transposing(self): """ Transposing the whole grid """ self.table = map(list, zip(*self.table)) def swap_rows_small(self): """ Swap the two rows """ area = random.randrange(0,self.n,1) line1 = random.randrange(0,self.n,1) # N1 = area*self.n + line1 # 1 line2 = random.randrange(0,self.n,1) # , while (line1 == line2): line2 = random.randrange(0,self.n,1) N2 = area*self.n + line2 # 2 self.table[N1],self.table[N2] = self.table[N2], self.table[N1] def swap_colums_small(self): grid.transposing(self) grid.swap_rows_small(self) grid.transposing(self) def swap_rows_area(self): """ Swap the two area horizon """ area1 = random.randrange(0,self.n,1) # area2 = random.randrange(0,self.n,1) # , while (area1 == area2): area2 = random.randrange(0,self.n,1) for i in range(0, self.n): N1, N2 = area1*self.n + i, area2*self.n + i self.table[N1], self.table[N2] = self.table[N2], self.table[N1] def swap_colums_area(self): grid.transposing(self) grid.swap_rows_area(self) grid.transposing(self) def mix(self,amt = 10): mix_func = ['self.transposing()', 'self.swap_rows_small()', 'self.swap_colums_small()', 'self.swap_rows_area()', 'self.swap_colums_area()'] for i in xrange(1, amt): id_func = random.randrange(0,len(mix_func),1) eval(mix_func[id_func]) example = grid() example.mix() flook = [[0 for j in range(example.n*example.n)] for i in range(example.n*example.n)] iterator = 0 difficult = example.n ** 4 # example.show() print "---------------------------" while iterator < example.n ** 4: i,j = random.randrange(0, example.n*example.n ,1), random.randrange(0, example.n*example.n ,1) # if flook[i][j] == 0: # iterator += 1 flook[i][j] = 1 # temp = example.table[i][j] # example.table[i][j] = 0 difficult -= 1 # table_solution = [] for copy_i in range(0, example.n*example.n): table_solution.append(example.table[copy_i][:]) # i_solution = 0 for solution in solver.solve_sudoku((example.n, example.n), table_solution): i_solution += 1 # if i_solution != 1: # example.table[i][j] = temp difficult += 1 # example.show() print "difficult = ",difficult solver.py
#!/usr/bin/env python3 # Author: Ali Assaf <ali.assaf.mail@gmail.com> # Copyright: (C) 2010 Ali Assaf # License: GNU General Public License <http://www.gnu.org/licenses/> from itertools import product def solve_sudoku(size, grid): """ An efficient Sudoku solver using Algorithm X. >>> grid = [ ... [5, 3, 0, 0, 7, 0, 0, 0, 0], ... [6, 0, 0, 1, 9, 5, 0, 0, 0], ... [0, 9, 8, 0, 0, 0, 0, 6, 0], ... [8, 0, 0, 0, 6, 0, 0, 0, 3], ... [4, 0, 0, 8, 0, 3, 0, 0, 1], ... [7, 0, 0, 0, 2, 0, 0, 0, 6], ... [0, 6, 0, 0, 0, 0, 2, 8, 0], ... [0, 0, 0, 4, 1, 9, 0, 0, 5], ... [0, 0, 0, 0, 8, 0, 0, 7, 9]] >>> for solution in solve_sudoku((3, 3), grid): ... print(*solution, sep='\\n') [5, 3, 4, 6, 7, 8, 9, 1, 2] [6, 7, 2, 1, 9, 5, 3, 4, 8] [1, 9, 8, 3, 4, 2, 5, 6, 7] [8, 5, 9, 7, 6, 1, 4, 2, 3] [4, 2, 6, 8, 5, 3, 7, 9, 1] [7, 1, 3, 9, 2, 4, 8, 5, 6] [9, 6, 1, 5, 3, 7, 2, 8, 4] [2, 8, 7, 4, 1, 9, 6, 3, 5] [3, 4, 5, 2, 8, 6, 1, 7, 9] """ R, C = size N = R * C X = ([("rc", rc) for rc in product(range(N), range(N))] + [("rn", rn) for rn in product(range(N), range(1, N + 1))] + [("cn", cn) for cn in product(range(N), range(1, N + 1))] + [("bn", bn) for bn in product(range(N), range(1, N + 1))]) Y = dict() for r, c, n in product(range(N), range(N), range(1, N + 1)): b = (r // R) * R + (c // C) # Box number Y[(r, c, n)] = [ ("rc", (r, c)), ("rn", (r, n)), ("cn", (c, n)), ("bn", (b, n))] X, Y = exact_cover(X, Y) for i, row in enumerate(grid): for j, n in enumerate(row): if n: select(X, Y, (i, j, n)) for solution in solve(X, Y, []): for (r, c, n) in solution: grid[r][c] = n yield grid def exact_cover(X, Y): X = {j: set() for j in X} for i, row in Y.items(): for j in row: X[j].add(i) return X, Y def solve(X, Y, solution): if not X: yield list(solution) else: c = min(X, key=lambda c: len(X[c])) for r in list(X[c]): solution.append(r) cols = select(X, Y, r) for s in solve(X, Y, solution): yield s deselect(X, Y, r, cols) solution.pop() def select(X, Y, r): cols = [] for j in Y[r]: for i in X[j]: for k in Y[i]: if k != j: X[k].remove(i) cols.append(X.pop(j)) return cols def deselect(X, Y, r, cols): for j in reversed(Y[r]): X[j] = cols.pop() for i in X[j]: for k in Y[i]: if k != j: X[k].add(i) if __name__ == "__main__": import doctest doctest.testmod() Work result
The base table is ready! [5, 4, 6, 8, 7, 9, 2, 1, 3] [8, 7, 9, 2, 1, 3, 5, 4, 6] [2, 1, 3, 5, 4, 6, 8, 7, 9] [6, 5, 7, 9, 8, 1, 3, 2, 4] [9, 8, 1, 3, 2, 4, 6, 5, 7] [3, 2, 4, 6, 5, 7, 9, 8, 1] [7, 6, 8, 1, 9, 2, 4, 3, 5] [1, 9, 2, 4, 3, 5, 7, 6, 8] [4, 3, 5, 7, 6, 8, 1, 9, 2] --------------------------- [0, 0, 6, 0, 0, 0, 0, 0, 0] [8, 7, 0, 0, 1, 0, 0, 0, 6] [0, 0, 0, 5, 4, 0, 0, 0, 9] [6, 0, 0, 0, 8, 1, 3, 0, 4] [0, 0, 0, 3, 0, 0, 0, 5, 0] [0, 0, 0, 0, 0, 7, 0, 0, 0] [0, 0, 0, 0, 0, 0, 0, 0, 0] [0, 9, 0, 4, 0, 0, 0, 0, 8] [0, 0, 5, 0, 6, 0, 1, 0, 0] difficult = 22 Download in zip
I am sure that there are more complex approaches in the construction of the Sudoku table. My goal was achieved, it turned out a working algorithm. Now I don’t need to look for new issues, I can generate them :)
In principle, a special case of Sudoku 9x9 was presented here. But there are no restrictions for using it on 16x16 and 25x25.
- Algorithm X and its implementation for Sudoku were used to verify the solution.
- Sudoku Solution in all languages http://rosettacode.org/wiki/Sudoku
If anyone has the best deals, feel free to leave a comment.
Thanks for attention.
Source: https://habr.com/ru/post/192102/
All Articles