The first few milliseconds of an https connection
After several hours of reading reviews, Bob eagerly pushed the transition button to place an order for a gallon of whole milk, and ...
Wow, what just happened?
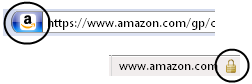
In 220 milliseconds a lot of interesting things happened, because of which Firefox changed the color of the address bar and displayed the lock in the lower right corner. Using my favorite Wireshark tool and a slightly modified Firefox debug build, we’ll try to figure out exactly what happened.
By RFC 2818, Firefox knows that "https" means that you need to use port 443 to connect to Amazon.com:

')
TLS wraps all traffic in a “record” of various types. We see that the first byte of the packet in HEX is 0x16 = 22, which means that the “record” is a “handshake”:

The next two bytes are 0x0301, meaning version 3.1, which means that TLS 1.0 is actually SSL 3.1.
A handshake entry is split into several messages. The first is “customer welcome” (0x01). Here are some important points:
Amazon.com responds with a rather large record with a two-packet handshake (2.551 bytes). It contains the same byte sequence 0x0301, which means Amazon’s consent to use TLS 1.0. There are three submissions with interesting data in the record:
Certificates are needed so that the browser can make sure that it communicates with Amazon.com. It looks at the start and end dates of the certificate, and also checks whether the public key is authorized to exchange secret keys.
Why do we have to trust certificates?
Attached is a “signature”, a long number in big-endian format:
Anyone could send these bytes. Why should we trust this signature? To answer, let's take a little trip to the world of mathematics:
Some people wonder if mathematics has anything to do with programming? Certificates - a very visual case of applying mathematics. The Amazon certificate tells us to use RSA to verify the signature. RSA was created in 1970 by professors MIT Ron Rivest, Adu Shamir and Len Adleman, who found a beautiful way to combine ideas that emerged over the 2000 years of mathematics and create a simple algorithm:
You choose two prime numbers, p and q. Multiply them and get n. Next, you choose a simple public exponent e, which will be an encryption exponent, and a specially chosen reverse e, d, which will be decryption. Then you make n and e public and keep d secret. You can forget about p and q, or keep it together with d.
Now, if you have a message, you just need to represent its bytes as the number M. If you need to encrypt the message, we calculate:
C ≡ M e (mod n)
This means that you need to multiply M by itself e times. mod n means that we take only the remainder of dividing by n. For example, 11 AM + 3 hours = 2PM (mod 12 hours). The recipient knows d and can perform the reverse operation to decrypt:
C d ≡ (M e ) d ≡ M e * d ≡ M 1 ≡ M (mod n)
It is also interesting that a person with d can sign a document raising the message M to the power of d:
M d ≡ S (mod n)
This is possible due to the fact that the signatory makes S, M, e, and n public. Anyone can verify the signature S using simple calculations:
S e ≡ (M d ) e ≡ M d * e ≡ M e * d ≡ M 1 ≡ M (mod n)
Public-key cryptography is often called asymmetric, because the encryption key (in our case e) is not equal to the decryption key (d). RSA magic works because you can calculate C ≡ M e (mod n) fairly quickly, but it’s almost impossible to C d ≡ M (mod n) without knowing d. As we have seen before, d is obtained from factorization n back to p and q, which is rather difficult.
When working with RSA in real life, it is important to remember that all numbers must be __ very __ large. How much? Amazon's certificate is signed by VeriSign Class 3 Secure Server CA. This means that n must be 2048 bits long, which is in decimal form:
1890572922 9464742433 9498401781 6528521078 8629616064 3051642608 4317020197 7241822595 6075980039 8371048211 4887504542 4200635317 0422636532 2091550579 0341204005 1169453804 7325464426 0479594122 4167270607 6731441028 3698615569 9947933786 3789783838 5829991518 1037601365 0218058341 7944190228 0926880299 3425241541 4300090021 1055372661 2125414429 9349272172 5333752665 6605550620 5558450610 3253786958 8361121949 2417723618 5199653627 5260212221 0847786057 9342235500 9443918198 9038906234 1550747726 8041766919 1500918876 1961879460 3091993360 6376719337 6644159792 1249204891 7079005527 7689341573 9395596650 5484628101 0469658502 1566385762 0175231997 6268718746 7514321
(Good luck with the selection of p and q. If it works, you can generate a fake VeriSign certificate.)
If we raise the signature S to the public e VeriSign degree, and then take the remainder of the division by the module n, then we get the decoded signature in hex:
0001FFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFF00302130 0906052B0E03021A 05000414C19F8786 871775C60EFE0542 E4C2167C830539DB
According to the PKCS # 1 v1.5 standard, the first byte 00 in order for the encryption block converted to an integer to be smaller than the module (they still didn’t understand what kind of module - approx. Transl.). The second byte 01 indicates that this is a private key operation. Then a bunch of FF bytes to fill in the empty space. It ends with byte 00, then the sequence “30 21 30 09 06 05 2B 0E 03 02 1A 05 00 04 14”, which means the use of the SHA-1 function. The last 20 bytes are the result of SHA-1 from bytes at signedCertificate.
Since the decoded value is correctly formatted and the last bytes correspond to what we can calculate ourselves, we can assume that someone who knows the private key “VeriSign Class 3 Secure Server CA” has signed it.
You can repeat the process and verify that the VeriSign Class 3 Secure Server CA certification was signed by the VeriSign Class 3 Public Primary Certification Authority.
But why trust him? There are no more links in this chain of trust.
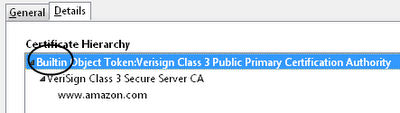
The root “VeriSign Class 3 Public Primary Certification Authority” was signed by itself. This certificate is embedded in Mozilla products as an unconditionally trusted certificate.
We checked Amazon.com and know its public encryption exponent e and module n. Anyone listening to us can do the same. Now we need to generate a random key that the attacker does not recognize. This is not as simple as it may seem, because of the vulnerability of the pseudo-generator of random numbers in Netscape Navigator 1.1 SSL could be hacked in 25 seconds on the machines of that time. If you don’t believe that real randomness is difficult, you can ask the OpenSSL maintainers in Debian.
On Windows, for example, the pseudo-random number generation function takes data from 125 sources. Firefox uses its result and adds a few bits of its own pseudo-random data.
It is very important to keep the 48-byte “pre-master key” secret, since many things are derived from it. No wonder Firefox is so hard to find. I had to build a debug version and set the SSLDEBUGFILE and SSLTRACE flags to see it.
4456: SSL [131491792]: Pre-Master Secret [Len: 48]
03 01 bb 7b 08 98 a7 49 de e8 e9 b8 91 52 ec 81 ... {... I ..... R ...
4c c2 39 7b f6 ba 1c 0a b1 95 50 29 be 02 ad e6 L.9 {...... P) ...
ad 6e 11 3f 20 c4 66 f0 64 22 57 7e e1 06 7a 3b .n.? .fd "W ~ ..z;
It is not completely random, the first two bytes of the TLS standard should be 03 01.
Key exchange
Now we need to transfer this secret number to Amazon.com. Since Amazon wanted to use „TLS_RSA_WITH_RC4_128_MD5“, we will encrypt it with RSA. You can use only 48 bytes of the pre-master key as a message, but according to the PKCS # 1 v1.5 standard, you need to fill in the empty space with random data and bring the packet size to 128 bytes. So it will be more difficult to decrypt the package to the attacker.
Finally, Firefox sends the last unencrypted message, the “Change Cipher Spec” entry:

This is the way Firefox tells Amazon that it is going to use the previously transmitted secret keys for the following messages.
Master Secret Calculation
If we did everything right, then both sides now know 48 bytes of the pre-master key. From the Amazon side, there is a slight distrust, since the pre-master contains only client data and does not contain server data. Fix this by calculating the master key.
master_secret = PRF (pre_master_secret, "master secret", ClientHello.random + ServerHello.random)
PRF is a pseudo-house function, which is defined in specifications and is quite tricky. It uses HMAC version MD5 and SHA-1. Half of the input is sent to each function, it turns out the result is very resistant to attacks.
As a result, we get 48 bytes of master secret.
4C AF 20 30 8F 4C AA C5 66 4A 02 90 F2 AC 10 00 39 DB 1D E0 1F CB E0 E0 9D D7 E6 BE 62 A4 6C 18 06 AD 79 21 DB 82 1D 53 84 DB 35 A7 1F C1 01 19
We generate other keys
Now that the two sides have a master secret, by specification we can calculate all the keys needed for the session using the PRF to create a “key block”, from which we take the necessary data:
key_block = PRF (SecurityParameters.master_secret, "key expansion", SecurityParameters.server_random + SecurityParameters.client_random);
Bytes from the "key block" are needed for:
client_write_MAC_secret [SecurityParameters.hash_size]
server_write_MAC_secret [SecurityParameters.hash_size]
client_write_key [SecurityParameters.key_material_length]
server_write_key [SecurityParameters.key_material_length]
client_write_IV [SecurityParameters.IV_size]
server_write_IV [SecurityParameters.IV_size]
Since we use streaming, not block encryption, we do not need initialization vectors. However, we need two Message Authentication Code (MAC) keys for each side, each 16 bytes, since the length of the MD5 result is also 16 bytes. In addition, RC4 uses a 16 byte key, which is also needed by both parties. In general, we need 2 * 16 + 2 * 16 = 64 bytes from the key block
Running PRF, we get:
client_write_MAC_secret = 80 B8 F6 09 51 74 EA DB 29 28 EF 6F 9A B8 81 B0
server_write_MAC_secret = 67 7C 96 7B 70 C5 BC 62 9D 1D 1F 4A A6 79 81 61
client_write_key = 32 13 2C DD 1B 39 36 40 84 4A DE E5 6C 52 46 72
server_write_key = 58 36 C4 0D 8C 7C 74 DA 6D B7 34 0A 91 B6 8F A7
Get ready to be encrypted!
The last message of the handshake sent by the client is the “Final Message”. This is a tricky message that proves that no one forged a handshake and proves that we know the key. The client takes all the bytes from the handshake messages and adds to the buffer. Then, 12 bytes of confirmation are calculated using the pseudo-random number generator, master key, “client finished” lines, and MD5 and SHA-1 from the buffer.
verify_data = PRF (master_secret, "client finished", MD5 (handshake_messages) + SHA-1 (handshake_messages))
We take the result and add bytes 0x14 to the header, indicating the completion, and bytes of length 00 00 0c to show that we are sending 12 bytes. Then, as in the future and for all encrypted messages, you need to make sure that no one forged the decrypted content. We use MD5, or rather its HMAC version.
HMAC_MD5 (Key, m) = MD5 ((Key ⊕ opad) ++ MD5 ((Key ⊕ ipad) ++ m)
(⊕ means XOR, ++ means concatenation, "opad" is bytes "5c 5c ... 5c", and "ipad" is bytes "36 36 ... 36").
In general, we calculate:
HMAC_MD5 (client_write_MAC_secret, seq_num + TLSCompressed.type + TLSCompressed.version + TLSCompressed.length + TLSCompressed.fragment));
As you can see, we mix the request number, which protects against a specific attack with a repetition of the packet.
It remains only to encrypt.
The selected set of encryption algorithms tells us to use RC4. It is so simple that you can learn it in a couple of minutes.
RC4 begins by creating a 256-byte array S and filling it with values from 0 to 255. Then you need to go through the array “interfering” the key bytes. This is done to create the state machine used to generate random bytes. Then we shuffle the array S.
Graphically, this can be represented as:

To encrypt a byte, we XOR a pseudo-random byte with a byte that needs to be encrypted.
So, everything is pretty simple, and works fast. It seems to me that because of this, Amazon chose this algorithm.
Recall that we have „client_write_key“ and „server_write_key“. This means that we need two copies of RC4: one to decrypt the answers, the other to encrypt requests.
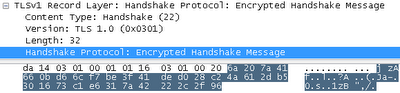
The first few random bytes from client_write are 7E 20 7A 4D FE FB 78 A7 33 .... If you look at these bytes with an unencrypted header and check the message bytes “14 00 00 0C 98 F0 AE CB C4 ...”, you will see what can be seen in the Wireshark screenshot below:
The server does almost the same thing. It sends a "Change Cipher Spec" and then a "final" message, which includes all the handshake messages and the unencrypted "final" message. This proves to the client that the server was able to decrypt its messages.
Now, after 220 milliseconds (three hours later - approx. Transl.), We are finally ready to use the application layer. Now you can exchange regular HTTP traffic that will be encrypted with TLS using RC4 and checked for cases of spoofing.
Now the handshake is complete. The contents of the TLS entry are now 0x17. Encrypted traffic starts from 17 03 01, which indicates the type of recording and the TLS version.
Encryption package:
GET /gp/cart/view.html/ref=pd_luc_mri HTTP / 1.1
Host: www.amazon.com
User-Agent: Mozilla / 5.0 (Windows; U; Windows NT 6.0; en-US; rv: 1.9.0.10) Gecko / 2009060911 Minefield / 3.0.10 (.NET CLR 3.5.30729)
Accept: text / html, application / xhtml + xml, application / xml; q = 0.9, * / *; q = 0.8
Accept-Language: en-us, en; q = 0.5
Accept-Encoding: gzip, deflate
Accept-Charset: ISO-8859-1, utf-8; q = 0.7, *; q = 0.7
Keep-Alive: 300
Connection: keep-alive
...
will give approximately the following result:

The server does the same. Decryption gives us the following:
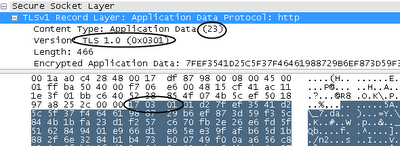
HTTP / 1.1 200 OK
Date: Wed, 10 Jun 2009 01:09:30 GMT
Server: Server
...
Conection: close
Transfer-Encoding: chunked
The connection remains open until either side sends a message warning of the termination and then closes the connection. If we reconnect shortly after closing the previous connection, we can use the old keys in order not to re-perform the handshake procedure.
It is important to understand that at the application level there can be absolutely anything. There are many other TCP / IP based protocols that can run on top of TLS. For example, FTPS. It is always better to use TLS instead of inventing your bike.
TLS RFC covers many details that we have not discussed. We only looked at a 220 millisecond dance between Firefox and Amazon. We learned that if someone decomposes the number n of Amazon into p and q, then he can decrypt all Amazon traffic until he changes the certificate.
In just 220 milliseconds, two points on the Internet connected, provided each other with enough data for trust, set up encryption algorithms, and began to exchange encrypted traffic.
And all so that Bob could buy milk.
Wow, what just happened?

In 220 milliseconds a lot of interesting things happened, because of which Firefox changed the color of the address bar and displayed the lock in the lower right corner. Using my favorite Wireshark tool and a slightly modified Firefox debug build, we’ll try to figure out exactly what happened.
By RFC 2818, Firefox knows that "https" means that you need to use port 443 to connect to Amazon.com:

')
Customer greeting
TLS wraps all traffic in a “record” of various types. We see that the first byte of the packet in HEX is 0x16 = 22, which means that the “record” is a “handshake”:

The next two bytes are 0x0301, meaning version 3.1, which means that TLS 1.0 is actually SSL 3.1.
A handshake entry is split into several messages. The first is “customer welcome” (0x01). Here are some important points:
- Accident:

These four bytes are the current Unix time, the number of seconds since January 1, 1970. In our case, this is 0x4a2f07ca. They are followed by 28 random bytes, which will be needed later. - Session ID:

In our case, this field is empty. If we connected to Amazon.com a few seconds earlier, we could continue the session and not hold a full handshake. - Cipher Suites:

A list of all browser-supported encryption algorithms. The default is a very strong TLS_ECDHE_ECDSA_WITH_AES_256_CBC_SHA, followed by another 33 options. Do not worry if you do not understand anything. Next, we learn that Amazon will not accept our default option. - Server_name extension:

The way to tell amazon.com is that the browser needs a page at www.amazon.com . This is quite convenient, because TLS handshake starts long before HTTP traffic. HTTP has a “Host” header that allows you to host hundreds of sites on the same IP. SSL has traditionally required different IPs for different sites, but this extension allows the server to respond with a specific site certificate.
Greeting server
Amazon.com responds with a rather large record with a two-packet handshake (2.551 bytes). It contains the same byte sequence 0x0301, which means Amazon’s consent to use TLS 1.0. There are three submissions with interesting data in the record:
- Server Welcome message:
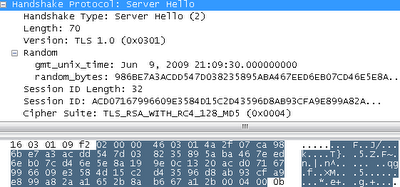
- Four bytes of Unix time and 28 random bytes.
- Session ID in 32 bytes to speed up the following requests.
- Of the 34 algorithms we proposed, Amazon chose TLS_RSA_WITH_RC4_128_MD5 (0x0004). This means that the RSA algorithm will be used to verify certificate signatures and key exchange, the RC4 algorithm to encrypt data, the MD5 hash function to verify the contents. We will discuss all of this in more detail later. It seems to me that Amazon has its own reasons for choosing these particular algorithms, for example, reducing the load on the CPU. A less likely option - thanks to Ron Rivest, the creator of all three of the above algorithms.
- Message with certificate:
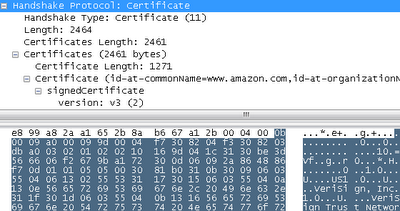
- A huge 2.464-byte message and its certificate that a client can use to validate an Amazon certificate. All this can also be viewed in the browser.
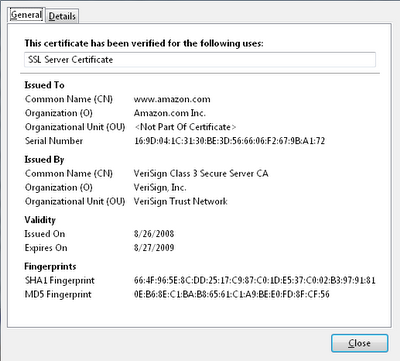
- A huge 2.464-byte message and its certificate that a client can use to validate an Amazon certificate. All this can also be viewed in the browser.
- The message "Server greeting is completed"

A blank message informs you that the greeting was successful and that the server will not request client certificates.
Certificate Verification
Certificates are needed so that the browser can make sure that it communicates with Amazon.com. It looks at the start and end dates of the certificate, and also checks whether the public key is authorized to exchange secret keys.
Why do we have to trust certificates?
Attached is a “signature”, a long number in big-endian format:

Anyone could send these bytes. Why should we trust this signature? To answer, let's take a little trip to the world of mathematics:
A little introduction to RSA
Some people wonder if mathematics has anything to do with programming? Certificates - a very visual case of applying mathematics. The Amazon certificate tells us to use RSA to verify the signature. RSA was created in 1970 by professors MIT Ron Rivest, Adu Shamir and Len Adleman, who found a beautiful way to combine ideas that emerged over the 2000 years of mathematics and create a simple algorithm:
You choose two prime numbers, p and q. Multiply them and get n. Next, you choose a simple public exponent e, which will be an encryption exponent, and a specially chosen reverse e, d, which will be decryption. Then you make n and e public and keep d secret. You can forget about p and q, or keep it together with d.
Now, if you have a message, you just need to represent its bytes as the number M. If you need to encrypt the message, we calculate:
C ≡ M e (mod n)
This means that you need to multiply M by itself e times. mod n means that we take only the remainder of dividing by n. For example, 11 AM + 3 hours = 2PM (mod 12 hours). The recipient knows d and can perform the reverse operation to decrypt:
C d ≡ (M e ) d ≡ M e * d ≡ M 1 ≡ M (mod n)
It is also interesting that a person with d can sign a document raising the message M to the power of d:
M d ≡ S (mod n)
This is possible due to the fact that the signatory makes S, M, e, and n public. Anyone can verify the signature S using simple calculations:
S e ≡ (M d ) e ≡ M d * e ≡ M e * d ≡ M 1 ≡ M (mod n)
Public-key cryptography is often called asymmetric, because the encryption key (in our case e) is not equal to the decryption key (d). RSA magic works because you can calculate C ≡ M e (mod n) fairly quickly, but it’s almost impossible to C d ≡ M (mod n) without knowing d. As we have seen before, d is obtained from factorization n back to p and q, which is rather difficult.
Signature verification
When working with RSA in real life, it is important to remember that all numbers must be __ very __ large. How much? Amazon's certificate is signed by VeriSign Class 3 Secure Server CA. This means that n must be 2048 bits long, which is in decimal form:
1890572922 9464742433 9498401781 6528521078 8629616064 3051642608 4317020197 7241822595 6075980039 8371048211 4887504542 4200635317 0422636532 2091550579 0341204005 1169453804 7325464426 0479594122 4167270607 6731441028 3698615569 9947933786 3789783838 5829991518 1037601365 0218058341 7944190228 0926880299 3425241541 4300090021 1055372661 2125414429 9349272172 5333752665 6605550620 5558450610 3253786958 8361121949 2417723618 5199653627 5260212221 0847786057 9342235500 9443918198 9038906234 1550747726 8041766919 1500918876 1961879460 3091993360 6376719337 6644159792 1249204891 7079005527 7689341573 9395596650 5484628101 0469658502 1566385762 0175231997 6268718746 7514321
(Good luck with the selection of p and q. If it works, you can generate a fake VeriSign certificate.)
If we raise the signature S to the public e VeriSign degree, and then take the remainder of the division by the module n, then we get the decoded signature in hex:
0001FFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFF00302130 0906052B0E03021A 05000414C19F8786 871775C60EFE0542 E4C2167C830539DB
According to the PKCS # 1 v1.5 standard, the first byte 00 in order for the encryption block converted to an integer to be smaller than the module (they still didn’t understand what kind of module - approx. Transl.). The second byte 01 indicates that this is a private key operation. Then a bunch of FF bytes to fill in the empty space. It ends with byte 00, then the sequence “30 21 30 09 06 05 2B 0E 03 02 1A 05 00 04 14”, which means the use of the SHA-1 function. The last 20 bytes are the result of SHA-1 from bytes at signedCertificate.
Since the decoded value is correctly formatted and the last bytes correspond to what we can calculate ourselves, we can assume that someone who knows the private key “VeriSign Class 3 Secure Server CA” has signed it.
You can repeat the process and verify that the VeriSign Class 3 Secure Server CA certification was signed by the VeriSign Class 3 Public Primary Certification Authority.
But why trust him? There are no more links in this chain of trust.

The root “VeriSign Class 3 Public Primary Certification Authority” was signed by itself. This certificate is embedded in Mozilla products as an unconditionally trusted certificate.
Pre-master Key
We checked Amazon.com and know its public encryption exponent e and module n. Anyone listening to us can do the same. Now we need to generate a random key that the attacker does not recognize. This is not as simple as it may seem, because of the vulnerability of the pseudo-generator of random numbers in Netscape Navigator 1.1 SSL could be hacked in 25 seconds on the machines of that time. If you don’t believe that real randomness is difficult, you can ask the OpenSSL maintainers in Debian.
On Windows, for example, the pseudo-random number generation function takes data from 125 sources. Firefox uses its result and adds a few bits of its own pseudo-random data.
It is very important to keep the 48-byte “pre-master key” secret, since many things are derived from it. No wonder Firefox is so hard to find. I had to build a debug version and set the SSLDEBUGFILE and SSLTRACE flags to see it.
4456: SSL [131491792]: Pre-Master Secret [Len: 48]
03 01 bb 7b 08 98 a7 49 de e8 e9 b8 91 52 ec 81 ... {... I ..... R ...
4c c2 39 7b f6 ba 1c 0a b1 95 50 29 be 02 ad e6 L.9 {...... P) ...
ad 6e 11 3f 20 c4 66 f0 64 22 57 7e e1 06 7a 3b .n.? .fd "W ~ ..z;
It is not completely random, the first two bytes of the TLS standard should be 03 01.
Key exchange
Now we need to transfer this secret number to Amazon.com. Since Amazon wanted to use „TLS_RSA_WITH_RC4_128_MD5“, we will encrypt it with RSA. You can use only 48 bytes of the pre-master key as a message, but according to the PKCS # 1 v1.5 standard, you need to fill in the empty space with random data and bring the packet size to 128 bytes. So it will be more difficult to decrypt the package to the attacker.
Finally, Firefox sends the last unencrypted message, the “Change Cipher Spec” entry:

This is the way Firefox tells Amazon that it is going to use the previously transmitted secret keys for the following messages.
Master Secret Calculation
If we did everything right, then both sides now know 48 bytes of the pre-master key. From the Amazon side, there is a slight distrust, since the pre-master contains only client data and does not contain server data. Fix this by calculating the master key.
master_secret = PRF (pre_master_secret, "master secret", ClientHello.random + ServerHello.random)
PRF is a pseudo-house function, which is defined in specifications and is quite tricky. It uses HMAC version MD5 and SHA-1. Half of the input is sent to each function, it turns out the result is very resistant to attacks.
As a result, we get 48 bytes of master secret.
4C AF 20 30 8F 4C AA C5 66 4A 02 90 F2 AC 10 00 39 DB 1D E0 1F CB E0 E0 9D D7 E6 BE 62 A4 6C 18 06 AD 79 21 DB 82 1D 53 84 DB 35 A7 1F C1 01 19
We generate other keys
Now that the two sides have a master secret, by specification we can calculate all the keys needed for the session using the PRF to create a “key block”, from which we take the necessary data:
key_block = PRF (SecurityParameters.master_secret, "key expansion", SecurityParameters.server_random + SecurityParameters.client_random);
Bytes from the "key block" are needed for:
client_write_MAC_secret [SecurityParameters.hash_size]
server_write_MAC_secret [SecurityParameters.hash_size]
client_write_key [SecurityParameters.key_material_length]
server_write_key [SecurityParameters.key_material_length]
client_write_IV [SecurityParameters.IV_size]
server_write_IV [SecurityParameters.IV_size]
Since we use streaming, not block encryption, we do not need initialization vectors. However, we need two Message Authentication Code (MAC) keys for each side, each 16 bytes, since the length of the MD5 result is also 16 bytes. In addition, RC4 uses a 16 byte key, which is also needed by both parties. In general, we need 2 * 16 + 2 * 16 = 64 bytes from the key block
Running PRF, we get:
client_write_MAC_secret = 80 B8 F6 09 51 74 EA DB 29 28 EF 6F 9A B8 81 B0
server_write_MAC_secret = 67 7C 96 7B 70 C5 BC 62 9D 1D 1F 4A A6 79 81 61
client_write_key = 32 13 2C DD 1B 39 36 40 84 4A DE E5 6C 52 46 72
server_write_key = 58 36 C4 0D 8C 7C 74 DA 6D B7 34 0A 91 B6 8F A7
Get ready to be encrypted!
The last message of the handshake sent by the client is the “Final Message”. This is a tricky message that proves that no one forged a handshake and proves that we know the key. The client takes all the bytes from the handshake messages and adds to the buffer. Then, 12 bytes of confirmation are calculated using the pseudo-random number generator, master key, “client finished” lines, and MD5 and SHA-1 from the buffer.
verify_data = PRF (master_secret, "client finished", MD5 (handshake_messages) + SHA-1 (handshake_messages))
We take the result and add bytes 0x14 to the header, indicating the completion, and bytes of length 00 00 0c to show that we are sending 12 bytes. Then, as in the future and for all encrypted messages, you need to make sure that no one forged the decrypted content. We use MD5, or rather its HMAC version.
HMAC_MD5 (Key, m) = MD5 ((Key ⊕ opad) ++ MD5 ((Key ⊕ ipad) ++ m)
(⊕ means XOR, ++ means concatenation, "opad" is bytes "5c 5c ... 5c", and "ipad" is bytes "36 36 ... 36").
In general, we calculate:
HMAC_MD5 (client_write_MAC_secret, seq_num + TLSCompressed.type + TLSCompressed.version + TLSCompressed.length + TLSCompressed.fragment));
As you can see, we mix the request number, which protects against a specific attack with a repetition of the packet.
It remains only to encrypt.
RC4 Encryption
The selected set of encryption algorithms tells us to use RC4. It is so simple that you can learn it in a couple of minutes.
RC4 begins by creating a 256-byte array S and filling it with values from 0 to 255. Then you need to go through the array “interfering” the key bytes. This is done to create the state machine used to generate random bytes. Then we shuffle the array S.
Graphically, this can be represented as:

To encrypt a byte, we XOR a pseudo-random byte with a byte that needs to be encrypted.
So, everything is pretty simple, and works fast. It seems to me that because of this, Amazon chose this algorithm.
Recall that we have „client_write_key“ and „server_write_key“. This means that we need two copies of RC4: one to decrypt the answers, the other to encrypt requests.
The first few random bytes from client_write are 7E 20 7A 4D FE FB 78 A7 33 .... If you look at these bytes with an unencrypted header and check the message bytes “14 00 00 0C 98 F0 AE CB C4 ...”, you will see what can be seen in the Wireshark screenshot below:

The server does almost the same thing. It sends a "Change Cipher Spec" and then a "final" message, which includes all the handshake messages and the unencrypted "final" message. This proves to the client that the server was able to decrypt its messages.
Welcome to the application layer!
Now, after 220 milliseconds (three hours later - approx. Transl.), We are finally ready to use the application layer. Now you can exchange regular HTTP traffic that will be encrypted with TLS using RC4 and checked for cases of spoofing.
Now the handshake is complete. The contents of the TLS entry are now 0x17. Encrypted traffic starts from 17 03 01, which indicates the type of recording and the TLS version.
Encryption package:
GET /gp/cart/view.html/ref=pd_luc_mri HTTP / 1.1
Host: www.amazon.com
User-Agent: Mozilla / 5.0 (Windows; U; Windows NT 6.0; en-US; rv: 1.9.0.10) Gecko / 2009060911 Minefield / 3.0.10 (.NET CLR 3.5.30729)
Accept: text / html, application / xhtml + xml, application / xml; q = 0.9, * / *; q = 0.8
Accept-Language: en-us, en; q = 0.5
Accept-Encoding: gzip, deflate
Accept-Charset: ISO-8859-1, utf-8; q = 0.7, *; q = 0.7
Keep-Alive: 300
Connection: keep-alive
...
will give approximately the following result:

The server does the same. Decryption gives us the following:

HTTP / 1.1 200 OK
Date: Wed, 10 Jun 2009 01:09:30 GMT
Server: Server
...
Conection: close
Transfer-Encoding: chunked
The connection remains open until either side sends a message warning of the termination and then closes the connection. If we reconnect shortly after closing the previous connection, we can use the old keys in order not to re-perform the handshake procedure.
It is important to understand that at the application level there can be absolutely anything. There are many other TCP / IP based protocols that can run on top of TLS. For example, FTPS. It is always better to use TLS instead of inventing your bike.
That's all!
TLS RFC covers many details that we have not discussed. We only looked at a 220 millisecond dance between Firefox and Amazon. We learned that if someone decomposes the number n of Amazon into p and q, then he can decrypt all Amazon traffic until he changes the certificate.
In just 220 milliseconds, two points on the Internet connected, provided each other with enough data for trust, set up encryption algorithms, and began to exchange encrypted traffic.
And all so that Bob could buy milk.
Source: https://habr.com/ru/post/191954/
All Articles