Solving the transport problem with a genetic algorithm as part of SOA

Solving the transport problem with a genetic algorithm as part of SOA

Greetings dear Habrasoobschestvo!

In this article I would like to talk about how I solved the transport problem using a genetic algorithm.
')

Task statement

Wikipedia formulates the task as follows - the problem of optimal transportation of a homogeneous product from homogeneous points of availability to homogeneous points of consumption on homogeneous vehicles (a predetermined quantity) with static data and a linear approach.

For example - it is necessary to plan the delivery of bottles of water in the city, the needs of each customer are known, the carrying capacity of vehicles and the distance between points.


Then you can add various restrictions - for example, delivery time windows, exclude certain machines from visiting certain points and so on. Add these and other restrictions in my immediate plans, but for now the service solves the problem formulated in the previous paragraph.

Genetic algorithm

Description

The solution is based on a parallel genetic algorithm. Each solution is represented by a chromosome, which can be crossed with another chromosome or mutated. As a result, the resulting child is added to the general population. The size of the population is limited and the least adapted chromosomes are removed.

A parallel algorithm is called because several isolated populations of chromosomes develop simultaneously. At certain points in time, randomly selected chromosomes move between populations.

Representation of chromosomes

Each chromosome is a solution to the problem and is presented in the form of an array of arrays, where each nested array represents one route (1 car’s trip). Each array element is a customer who needs to deliver cargo:


All routes obviously begin with a warehouse and implicitly end with them.

Crossbreeding

We have 2 types of crossings - random (Random Crossover) and homogeneous (Uniform Crossover)
Random crossing is an arbitrary part of an arbitrary route from parent 1 placed in the best insertion point for parent 2. The best insertion point is the one that gives the shortest length.


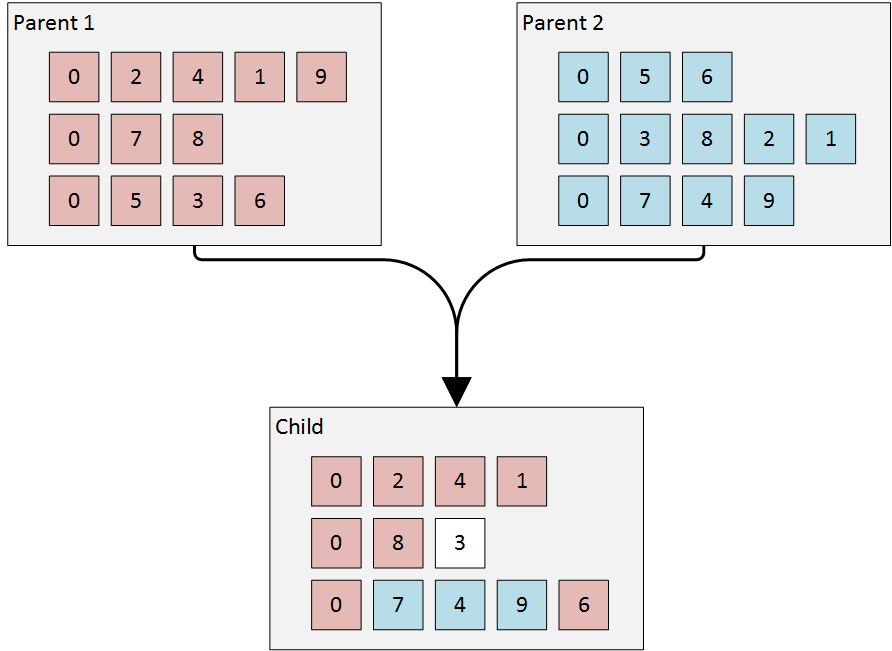
Homogeneous crossing computes density indices for all routes of parents and in turn adds routes with the lowest index from parents 1 and 2. The remaining points are distributed to the best insertion points.

Mutations

The algorithm uses 2 types of mutations - random and directed to the most distant parts of the route mutation.
Random mutations cut out part of the random part of the route and insert it into a place that gives the minimum total distance. The second type of mutation finds the most distant clients in random routes and moves it to the place of the best insert.

Local optimization

After crossing and mutation operations, the algorithm tries to move the points of each route in such a way that the length of the route is minimal.

Fitness function

The fitness (quality) of each chromosome is calculated by the formula:
Fitness = total distance + penalty for overloading * overloading + penalty for underloading * underloading

Maintain route uniqueness

For a faster solution, only unique chromosomes are contained within each group.

End of calculations

The algorithm completes the calculations to achieve the maximum number of epochs or, in the absence of improvements over a certain% of epochs.

The results of the algorithm

Below are the results of the algorithm on a subset of the standard set of tasks. The first digit in the title of the problem is the number of points, the second is the min number of cars. B-n31-k5 - 31 points with 5 machines.
The results of work on 8 core AMD (8350):


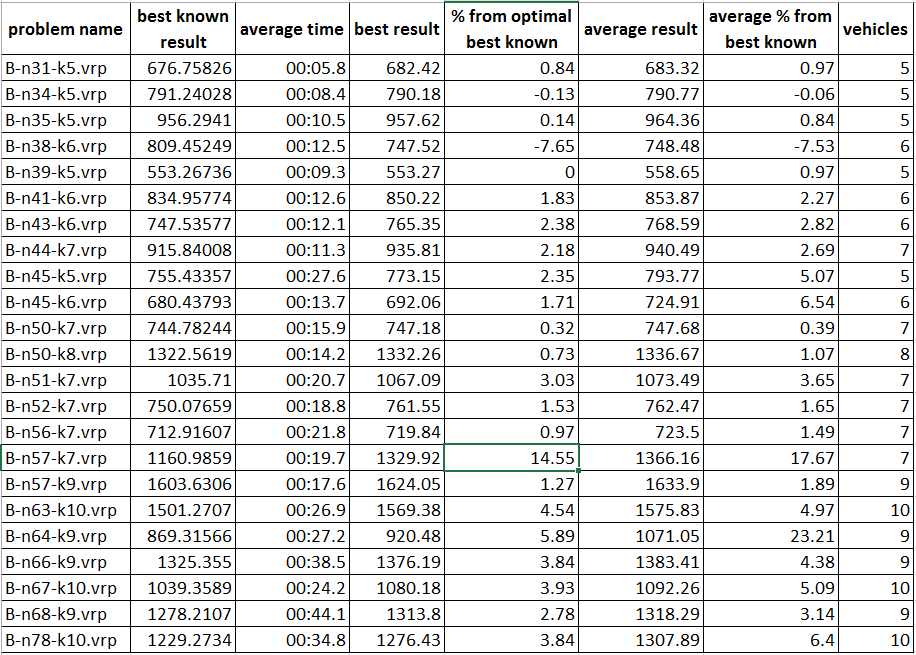
The results of work on all test data are on the project page.

Solution Architecture

The solution is written in C # and consists of a number of services, databases and queues:


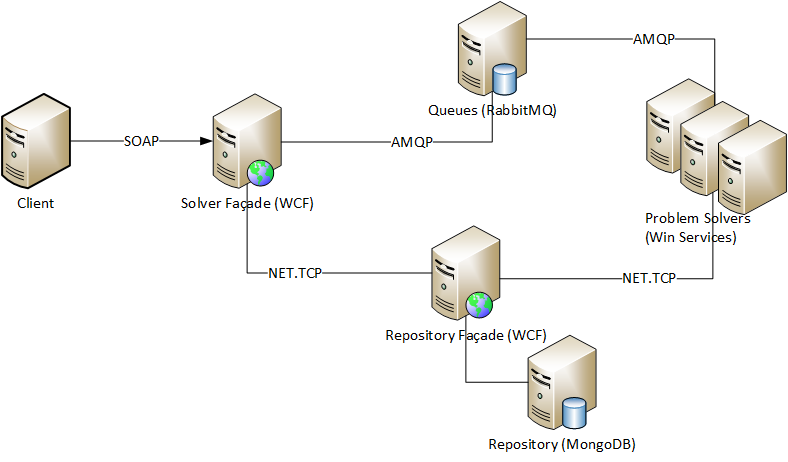
Technology stack:
1. .NET 4.5 / C # / WCF / WinService
2. Queue: RabbitMQ
3. DB: MongoDB
4. DI container: Autofac
5. Unit tests: MS Test / Rhino Mocks / Fluent assertions

.NET specific experience that I consider necessary to share:
1. In the frequently reversed code sections, do not use properties, but simply public variables.
2. Arrays are often faster than lists (List) and dictionaries (Dictionary) even when they are inserted into and deleted items

Next steps

The current solution is available for free.
The list of new functionality which is under development:
1. Getting distances by coordinates of points
2. Adding restrictions - by time windows, cars and points of delivery

Bibliography

Google contains a lot of publications about the solution of the problem by means of genetic (and not only) algorithms. Here are the names of some of them:
1. Solving the Vehicle Routing Problem with Genetic Algorithms
2. A hybrid algorithm for the Vehicle Routing Problem with Time Windows
3. A Route-Driving Hybrid Generic Approach for the Vehicle Routing Problem with Time Windows