How to generate random bracket sequences
Hi, Habr!
When testing algorithms, I often have a problem to generate a random binary tree. Moreover, Wishlist is not reduced to any random tree, but taken from a uniform distribution. Despite the seeming simplicity, to effectively build such a tree is not at all trivial.
The title of this article contains the words "bracket sequence". There is something more behind these words, because with the help of brackets one can describe very diverse objects, including binary trees. On Habré a separate post was devoted to this fact.
')
In this article, I will discuss several ways to generate a random bracket sequence, including in linear time, and then give an example of converting a sequence into a binary tree. Interesting?
Given a given n, generate the correct bracket sequence according to a uniform distribution over all correct sequences of length 2 n .
It is known that the number of regular bracket sequences of length 2 n is equal to the nth Catalan number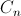 . To calculate the numbers Catalan exist explicit
. To calculate the numbers Catalan exist explicit

and recursive
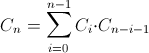
formulas.
We need a random number generator. For a given n , it will generate an equally probable random number from 0 to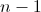 . We also need a random permutation generator above lists. In python, it is called random.shuffle. It will be enough for us that it works in linear time and on the sequence 1,2, ..., n generates a random permutation according to a uniform distribution.
. We also need a random permutation generator above lists. In python, it is called random.shuffle. It will be enough for us that it works in linear time and on the sequence 1,2, ..., n generates a random permutation according to a uniform distribution.
There is such an idea that all correct bracket sequences can be numbered. And, for example, there is a detailed description of how to do this. So, you can implement such a plan.
The plan is almost perfect. Those. the plan is quite good, if n is small, less than 30. But if n turns out to be about 1,000, you need long arithmetic, the algorithms by reference instead of the promised square will work cubic time, and in general, dynamic programming is not good for you. I think we will have to sweat a lot to meet this plan, at least in . Let's look for alternative ways.
. Let's look for alternative ways.
Take another look at the explicit formula for the Catalan numbers.
 .
.
In fact, it means that there are a lot of correct bracket sequences.
We will call a sequence balanced if the number of opening and closing brackets in it is the same. For example, the sequences . If you randomly select one of these sequences, then it will be correct with probability
. If you randomly select one of these sequences, then it will be correct with probability 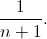
New plan.
Let's start with the first paragraph: how to generate such a random bracket sequence. Let's take an arbitrary balanced sequence and shuffle it through random.shuffle.
If you sit with a piece of paper and a pen, you can understand that for any balanced bracket sequence x exists exactly permutations that translate an arbitrary initial balanced sequence to x . This means that random.shuffle generates any balanced sequence with equal probability. We get the algorithm.
permutations that translate an arbitrary initial balanced sequence to x . This means that random.shuffle generates any balanced sequence with equal probability. We get the algorithm.
It remains to estimate the time of work. The correct and random.shuffle procedures work per line. How many iterations will be the main loop? We know that the correct bracket sequence is generated with probability . Then we can say that we have a coin, in which the eagle falls out with probability
. Then we can say that we have a coin, in which the eagle falls out with probability  . It is necessary to calculate the mathematical expectation of the number of throws until the eagle falls out.
. It is necessary to calculate the mathematical expectation of the number of throws until the eagle falls out.
Alternatively, you can paint the expectation of the formula and get something like this:

Or take advantage of well-known facts . One way or another, mat. the waiting time of the entire algorithm will be .
.
Well, but what if we need a really big sequence? Sequence per million characters.
The linear algorithm is no longer so trivial. Back in 1992, a separate article by Mike Atkinson and Georges Seck was devoted to him. I will state here my vision of what is written in the article.
We need a magic function f . The input function must take a balanced bracket sequence, and the output to return the correct same length. It is important to make the function scatter the sequences evenly, namely, for each correct sequence y there was exactly n +1 balanced sequence x , such that f (x) = y . If the function can be calculated for linear time, then the matter is in the hat.
We generate bracket bracket sequence x according to uniform distribution and return f (x).
All the trick in the function. If you want, you can stop and try to come up with one yourself. It does not work, nothing terrible. Now I will get a rabbit from the world of mathematics from the cylinder, and everyone will be fine.
Suppose we have a counter, and initially it is zero. Run through the sequence. For each opening bracket we will add a point, for each closing - to subtract.
The graph below shows how the
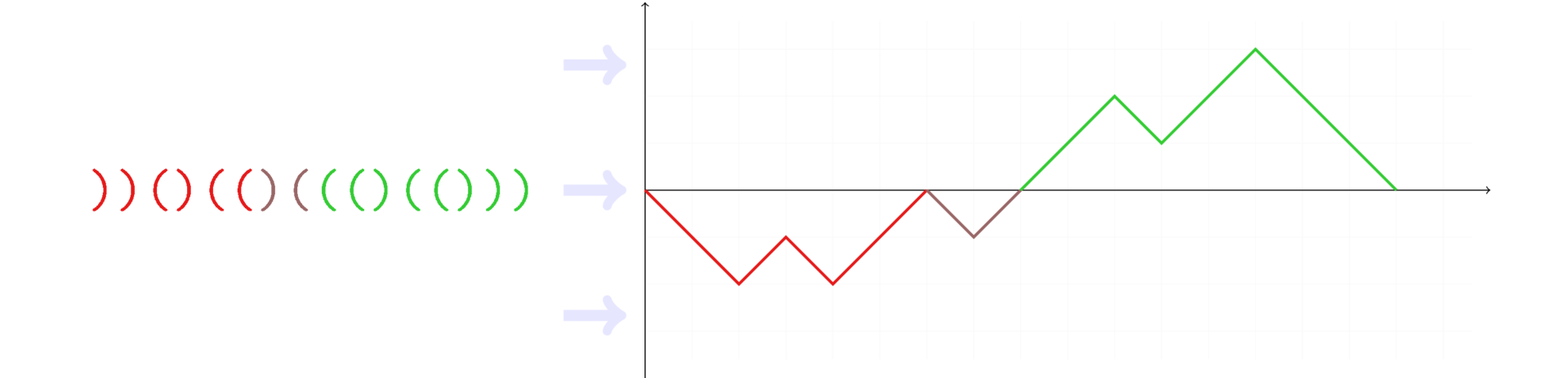
Sequences colored with individual colors are called indecomposable. Those. In general, a sequence is indecomposable if the counter on it takes a zero value only at the starting and ending point. You can see that indecomposable sequences fall into two categories: those that lie entirely above the zero level, and those that are lower. The first will be called positive sequences, the second - negative.
Calculate the total length of negative subsequences and divide it in half. The resulting value is called a sequence defect. The correct sequences have zero defect. If we replace all the brackets in the correct sequence of length 2 n with inverse, the defect will be n .
Attention, rabbit! Chang-Feller theorem. The number of bracket sequences of length 2 n with defect k is equal to the n- th Catalan number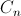 and does not depend on k .
and does not depend on k .
The theorem is interesting in that it breaks all balanced sequences of length 2 n into n + 1 classes of the same size, and among the classes there is a separate one containing all the correct bracket sequences. So, you can try to come up with a function that would encode each sequence x with defect k with the correct sequence y , and you could unambiguously reconstruct x using the sequence y and defect k .
If we manage to come up with such a function, then we get that for every correct sequence there are exactly n + 1 balanced with defects from 0 to n . It seems simple.
Let's take all negative subsequences and invert them, i.e. replace brackets with opposite ones.
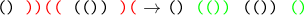
Plus such a function, it retains the positions of all indecomposable sequences. Minus - we lose all the information about which subsequence was negative and which is positive. Even knowing that the defect was 3, we cannot restore the initial sequence from the example.
Let's reverse all negative subsequences, and then move them to the end.

Now, knowing the defect, we can recover the negative subsequences. But we lost the position where they were.
Take an arbitrary indecomposable negative sequence and tear off the extreme brackets from it, and invert the result.
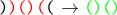
We call this operation tricky inversion and denote it by g . Because the sequence is indecomposable and negative, the result will always be the correct bracket sequence. The trick of g is that, on the one hand, it is reversible, and on the other, we have two extra brackets with which we can encode the position of a negative subsequence.
We finish Attempt 2, but now we take out the negative sequences in the reverse order and slyly invert them through the function g :
![\ texttt {() {\ color {red})) ((} (()) {\ color {red}) (}} \ rightarrow \ texttt {() {\ color {blue} \ bf [} (() ) {\ color {blue} \ bf [} {\ color {blue} \ bf]} {\ color {green} e}} _ {\ texttt {\ color {red}) (}} \ texttt {{\ color {blue} \ bf]} {\ color {green} ()}} _ \ texttt {\ color {red})) ((}](https://habrastorage.org/getpro/habr/post_images/e07/77b/0aa/e0777b0aa19cbdad72a0f21933700520.gif)
As can be seen from the example, the position of the negative subsequence can be noted in the released brackets. I have them highlighted in blue and made square. The letter e means an empty sequence.
Find out which brackets are green and which blue ones can be by defect, which means that you can restore the initial sequence itself. This is what you need!
Atkinson and Sack proposed a recursive formula for the function f:
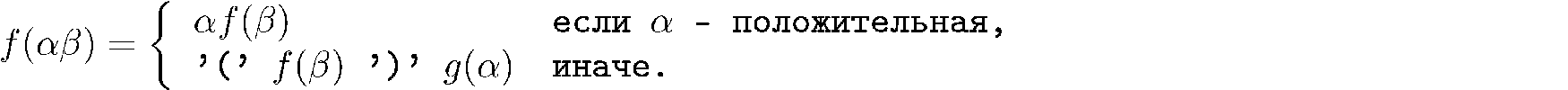
Here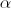 indecomposable subsequence, and
indecomposable subsequence, and 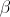 - the remainder.
- the remainder.
Below I enclose the implementation of the algorithm on Python with expanded recursion. It is easy to understand that the algorithm works linear time.
If you have read this far, I am very happy. All that's left is to convert the sequence to a tree.
The bracket sequences of length 2 n perfectly encode trees of arbitrary arity with n + 1 vertices. Indeed, run the search in depth. When entering a vertex, we write an opening bracket, at the exit - a closing one.
At the same time, trees of arbitrary arity from n + 1 can be put in one-to-one correspondence with binary trees from n vertices. All that is needed is to first write down trees of arbitrary arity in the form of “left child - right neighbor”, and then rename the right neighbor to right child.
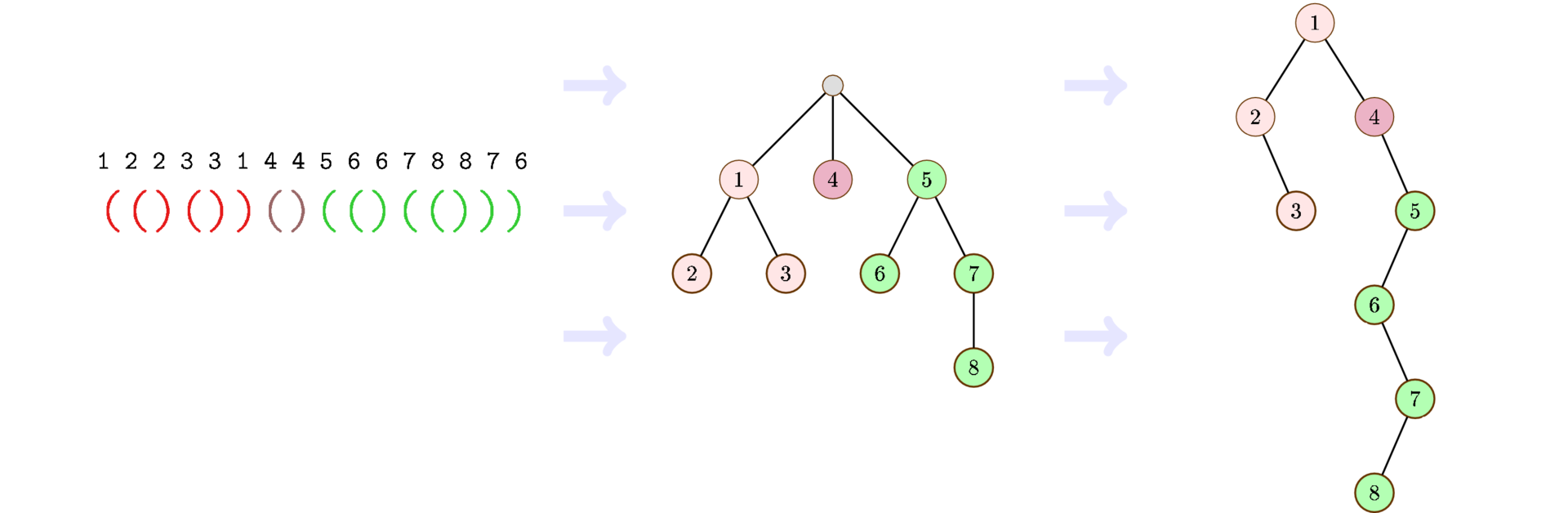
Thank you for being with us!
When testing algorithms, I often have a problem to generate a random binary tree. Moreover, Wishlist is not reduced to any random tree, but taken from a uniform distribution. Despite the seeming simplicity, to effectively build such a tree is not at all trivial.
The title of this article contains the words "bracket sequence". There is something more behind these words, because with the help of brackets one can describe very diverse objects, including binary trees. On Habré a separate post was devoted to this fact.
')
In this article, I will discuss several ways to generate a random bracket sequence, including in linear time, and then give an example of converting a sequence into a binary tree. Interesting?
Task
Given a given n, generate the correct bracket sequence according to a uniform distribution over all correct sequences of length 2 n .
Inventory
It is known that the number of regular bracket sequences of length 2 n is equal to the nth Catalan number
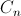 . To calculate the numbers Catalan exist explicit
. To calculate the numbers Catalan exist explicit
and recursive
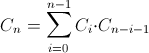
formulas.
We need a random number generator. For a given n , it will generate an equally probable random number from 0 to
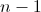 . We also need a random permutation generator above lists. In python, it is called random.shuffle. It will be enough for us that it works in linear time and on the sequence 1,2, ..., n generates a random permutation according to a uniform distribution.
. We also need a random permutation generator above lists. In python, it is called random.shuffle. It will be enough for us that it works in linear time and on the sequence 1,2, ..., n generates a random permutation according to a uniform distribution.Three ways to say "Avos"
Dynamic programming forces
There is such an idea that all correct bracket sequences can be numbered. And, for example, there is a detailed description of how to do this. So, you can implement such a plan.
- We consider the n-th number of Catalan.
- We generate a random number from 1 to
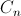 .
. - By the forces of dynamic programming and combinatorial counting, we restore the bracket sequence by its number.
The plan is almost perfect. Those. the plan is quite good, if n is small, less than 30. But if n turns out to be about 1,000, you need long arithmetic, the algorithms by reference instead of the promised square will work cubic time, and in general, dynamic programming is not good for you. I think we will have to sweat a lot to meet this plan, at least in
 . Let's look for alternative ways.
. Let's look for alternative ways.Try and check
Take another look at the explicit formula for the Catalan numbers.
 .
.In fact, it means that there are a lot of correct bracket sequences.
We will call a sequence balanced if the number of opening and closing brackets in it is the same. For example, the sequences
")(()" , "()()" are balanced, and the sequence "()))" is not. Obviously, any correct sequence is balanced. Total of all possible balanced sequences of length 2n exists  . If you randomly select one of these sequences, then it will be correct with probability
. If you randomly select one of these sequences, then it will be correct with probability 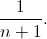
New plan.
- We generate a random balanced bracket sequence according to a uniform distribution.
- We check it for correctness.
- If the sequence is correct, then output. If not, then go back to step 1.
Let's start with the first paragraph: how to generate such a random bracket sequence. Let's take an arbitrary balanced sequence and shuffle it through random.shuffle.
seq = ['(', ')'] * n random.shuffle(seq) If you sit with a piece of paper and a pen, you can understand that for any balanced bracket sequence x exists exactly
 permutations that translate an arbitrary initial balanced sequence to x . This means that random.shuffle generates any balanced sequence with equal probability. We get the algorithm.
permutations that translate an arbitrary initial balanced sequence to x . This means that random.shuffle generates any balanced sequence with equal probability. We get the algorithm. def tryAndCheck(n): seq = [')', '('] * n while (not correct(seq)): random.shuffle(seq) return seq It remains to estimate the time of work. The correct and random.shuffle procedures work per line. How many iterations will be the main loop? We know that the correct bracket sequence is generated with probability
 . Then we can say that we have a coin, in which the eagle falls out with probability
. Then we can say that we have a coin, in which the eagle falls out with probability  . It is necessary to calculate the mathematical expectation of the number of throws until the eagle falls out.
. It is necessary to calculate the mathematical expectation of the number of throws until the eagle falls out.Alternatively, you can paint the expectation of the formula and get something like this:

Or take advantage of well-known facts . One way or another, mat. the waiting time of the entire algorithm will be
 .
.Try and correct
Well, but what if we need a really big sequence? Sequence per million characters.
The linear algorithm is no longer so trivial. Back in 1992, a separate article by Mike Atkinson and Georges Seck was devoted to him. I will state here my vision of what is written in the article.
We need a magic function f . The input function must take a balanced bracket sequence, and the output to return the correct same length. It is important to make the function scatter the sequences evenly, namely, for each correct sequence y there was exactly n +1 balanced sequence x , such that f (x) = y . If the function can be calculated for linear time, then the matter is in the hat.
We generate bracket bracket sequence x according to uniform distribution and return f (x).
All the trick in the function. If you want, you can stop and try to come up with one yourself. It does not work, nothing terrible. Now I will get a rabbit from the world of mathematics from the cylinder, and everyone will be fine.
Suppose we have a counter, and initially it is zero. Run through the sequence. For each opening bracket we will add a point, for each closing - to subtract.
balance = 0 for c in seq: balance += 1 if c == '(' else -1 The graph below shows how the
balance counter changes as you move along the sequence.
Sequences colored with individual colors are called indecomposable. Those. In general, a sequence is indecomposable if the counter on it takes a zero value only at the starting and ending point. You can see that indecomposable sequences fall into two categories: those that lie entirely above the zero level, and those that are lower. The first will be called positive sequences, the second - negative.
Calculate the total length of negative subsequences and divide it in half. The resulting value is called a sequence defect. The correct sequences have zero defect. If we replace all the brackets in the correct sequence of length 2 n with inverse, the defect will be n .
Attention, rabbit! Chang-Feller theorem. The number of bracket sequences of length 2 n with defect k is equal to the n- th Catalan number
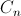 and does not depend on k .
and does not depend on k .The theorem is interesting in that it breaks all balanced sequences of length 2 n into n + 1 classes of the same size, and among the classes there is a separate one containing all the correct bracket sequences. So, you can try to come up with a function that would encode each sequence x with defect k with the correct sequence y , and you could unambiguously reconstruct x using the sequence y and defect k .
If we manage to come up with such a function, then we get that for every correct sequence there are exactly n + 1 balanced with defects from 0 to n . It seems simple.
Attempt 1.
Let's take all negative subsequences and invert them, i.e. replace brackets with opposite ones.
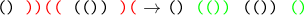
Plus such a function, it retains the positions of all indecomposable sequences. Minus - we lose all the information about which subsequence was negative and which is positive. Even knowing that the defect was 3, we cannot restore the initial sequence from the example.
Attempt 2.
Let's reverse all negative subsequences, and then move them to the end.

Now, knowing the defect, we can recover the negative subsequences. But we lost the position where they were.
Attempt 3.
Take an arbitrary indecomposable negative sequence and tear off the extreme brackets from it, and invert the result.
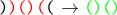
We call this operation tricky inversion and denote it by g . Because the sequence is indecomposable and negative, the result will always be the correct bracket sequence. The trick of g is that, on the one hand, it is reversible, and on the other, we have two extra brackets with which we can encode the position of a negative subsequence.
We finish Attempt 2, but now we take out the negative sequences in the reverse order and slyly invert them through the function g :
![\ texttt {() {\ color {red})) ((} (()) {\ color {red}) (}} \ rightarrow \ texttt {() {\ color {blue} \ bf [} (() ) {\ color {blue} \ bf [} {\ color {blue} \ bf]} {\ color {green} e}} _ {\ texttt {\ color {red}) (}} \ texttt {{\ color {blue} \ bf]} {\ color {green} ()}} _ \ texttt {\ color {red})) ((}](https://habrastorage.org/getpro/habr/post_images/e07/77b/0aa/e0777b0aa19cbdad72a0f21933700520.gif)
As can be seen from the example, the position of the negative subsequence can be noted in the released brackets. I have them highlighted in blue and made square. The letter e means an empty sequence.
Find out which brackets are green and which blue ones can be by defect, which means that you can restore the initial sequence itself. This is what you need!
Atkinson and Sack proposed a recursive formula for the function f:
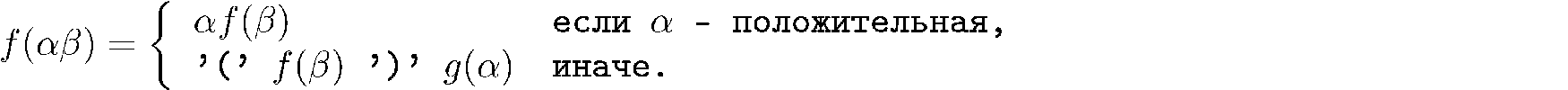
Here
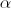 indecomposable subsequence, and
indecomposable subsequence, and 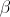 - the remainder.
- the remainder.Below I enclose the implementation of the algorithm on Python with expanded recursion. It is easy to understand that the algorithm works linear time.
def tryAndFix(n): seq = ['(', ')'] * n random.shuffle(seq) stack = [] result = [] balance = 0 prev = 0 for pos in range( len(seq) ): balance += 1 if seq[pos] == '(' else -1 if balance == 0: if seq[prev] == '(': result.extend( seq[ prev : pos + 1 ] ) else: result.append('(') stack.append( [ ')' if v == '(' else '(' for v in seq[ prev + 1 : pos ] ] ) prev = pos + 1 for lst in reversed(stack): result.append(')') result.extend(lst) return result Tree generation
If you have read this far, I am very happy. All that's left is to convert the sequence to a tree.
The bracket sequences of length 2 n perfectly encode trees of arbitrary arity with n + 1 vertices. Indeed, run the search in depth. When entering a vertex, we write an opening bracket, at the exit - a closing one.
At the same time, trees of arbitrary arity from n + 1 can be put in one-to-one correspondence with binary trees from n vertices. All that is needed is to first write down trees of arbitrary arity in the form of “left child - right neighbor”, and then rename the right neighbor to right child.

Thank you for being with us!
Links
- "Uniform Random Generation of Balanced Parenthesis Strings" DB Arnold, MR Sleep, 1980 - the first article on the generation of random bracket sequences.
- "Generating binary trees at random" MD Atkinson, J.-R. Sack, 1992
- Script on Pastin
Source: https://habr.com/ru/post/191298/
All Articles