Meet-in-the-middle: brute force optimization and more
In the last article I wrote about heuristic brute force optimization. In this article I will tell you about another, but already asymptotic optimization - meet-in-the-middle.
Typical for this method of reducing the asymptotics:
and 
.
The method is to divide the task in half, get some data and compare it with each other.
')
It makes sense to use meet-in-the-middle if two conditions are met for a specific task:
1) The processing time for half the data is asymptotically less than the time for obtaining the final answer.
2) There is an asymptotically faster way to get an answer for the whole task using information about processing its halves.
In order for understanding to emerge, it is best to look at examples (given in order of increasing perceived complexity):
Given N numbers. It is necessary to choose k numbers so that their sum is equal to 0 (the same elements can be used several times).
Naive solution:
Go through all
choices k numbers, recalculating the amount in the course of recursion. Asymptotics: 
.
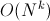Meet-in-the-middle solution for even k :
1) Mentally divide the k numbers to be found into two piles of k / 2.
2.1) write out all
amounts
2.2) Sort the array of sums.
2.3) For each sum s, we try to find a binary search - s .
2.4) If found, then here it is, our answer. If not, then such a combination does not exist.
3) Profit: .
To change this algorithm for odd k , I think, is not difficult for you.
If N = 30 and k = 12, then the meet-in-the-middle will work for about a minute, and the naive algorithm will last 17 years.
The magician has a deck of 36 playing cards. Initially, they are in the order of 1, 2, 3 ..., and he wants to get some kind of specific permutation, and not more than k steps. At each step, the magician shifts m cards in succession to the beginning of the deck.
The task is to find out whether he can get the desired permutation.
We define the state graph S as a graph in which the vertices are given by the current permutation of the maps, and the edges by the ability to go from one permutation to another in 1 step. It is worth noting that in this column 36!
vertices, but from each vertex there is a 36- m +1 edge, which is relatively few.
Naive solution:
Run a wide search on the state graph S. If you have reached the desired state or to the vertex remote by k +1, then complete the search. Asymptotics:
.
Meet-in-the-middle solution:
1) Run two searches in width from the initial and final vertices with a maximum depth of k / 2. We write two sets: all the states that have been searched in width.
2) If these sets intersect, then there is a path, if not, then there is no path.
3) Profit: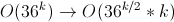
.
I hope I was able to lucidly explain the concept of meet-in-the-middle. If you have any questions - ask in the comments, I will try to answer. Thanks for attention.
Typical for this method of reducing the asymptotics:
and .Introduction
The method is to divide the task in half, get some data and compare it with each other.
')
It makes sense to use meet-in-the-middle if two conditions are met for a specific task:
1) The processing time for half the data is asymptotically less than the time for obtaining the final answer.
2) There is an asymptotically faster way to get an answer for the whole task using information about processing its halves.
In order for understanding to emerge, it is best to look at examples (given in order of increasing perceived complexity):
Example # 1: Optimization of brute force
Given N numbers. It is necessary to choose k numbers so that their sum is equal to 0 (the same elements can be used several times).
Naive solution:
Go through all
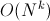choices k numbers, recalculating the amount in the course of recursion. Asymptotics: .Meet-in-the-middle solution for even k :
1) Mentally divide the k numbers to be found into two piles of k / 2.
2.1) write out all
amounts2.2) Sort the array of sums.
2.3) For each sum s, we try to find a binary search - s .
2.4) If found, then here it is, our answer. If not, then such a combination does not exist.
3) Profit:
.To change this algorithm for odd k , I think, is not difficult for you.
If N = 30 and k = 12, then the meet-in-the-middle will work for about a minute, and the naive algorithm will last 17 years.
Example # 2: Optimizing the shortest path search in a huge state graph
The magician has a deck of 36 playing cards. Initially, they are in the order of 1, 2, 3 ..., and he wants to get some kind of specific permutation, and not more than k steps. At each step, the magician shifts m cards in succession to the beginning of the deck.
Picture for explanation
The task is to find out whether he can get the desired permutation.
We define the state graph S as a graph in which the vertices are given by the current permutation of the maps, and the edges by the ability to go from one permutation to another in 1 step. It is worth noting that in this column 36!
vertices, but from each vertex there is a 36- m +1 edge, which is relatively few.Naive solution:
Run a wide search on the state graph S. If you have reached the desired state or to the vertex remote by k +1, then complete the search. Asymptotics:
.Meet-in-the-middle solution:
1) Run two searches in width from the initial and final vertices with a maximum depth of k / 2. We write two sets: all the states that have been searched in width.
2) If these sets intersect, then there is a path, if not, then there is no path.
3) Profit:
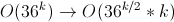.Example # 3: Counting the number of “good” subsets
For students and those who want to break the brain
Given a graph G ( N vertices). It is required to count the number of complete subgraphs of the graph G (click).
Naive solution:
Go through all
subgraphs and check for the square that it is a click. Asymptotics: 
.
This algorithm can be improved to
. To do this, you need to store a mask of vertices in the recursive search function, which we can still add. By supporting this mask, you can add only the "necessary" vertices, and then, at the end, you will not need to check the subgraph for what it is - a click. You can add a vertex for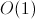 
, using the bitwise "and" of the current mask and the rows of the adjacency matrix of the added vertex.
The solution to meet-in-the-middle.
1.1) We divide the graph G into 2 graphs G1 and G2 by N / 2 vertices. Find for
all clicks in each of them. Asymptotics: .
Now it is necessary to find out for each click of the G1 graph the number of clicks of the G2 graph, such that their union is a click. Their sum is the final answer.
Since for a single clique K of the graph G1 there may be several suitable clicks in G2 , then using the same method as in the previous two examples will not work. But the only object for the clique K is the mask of the vertices of the graph G2 , which can still be added. We have a lot of time for pre-counting and this needs to be used: for each such mask in G2, you need to pre-calculate the answer, namely:
1.2) Using the dynamic programming method, for each mask of the vertices of the G2 graph, the number of clicks whose vertices are a subset of the selected mask is assumed. Number of states: . Number of transitions: 
. Asymptotics: 
.
Here is the Python translation:
2) For each click of K (including an empty one) of the G1 graph, we add to the global answer the calculated number of clicks that can be added to K (including empty ones). Asymptotics: .
3) Profit:
.
Naive solution:
Go through all
subgraphs and check for the square that it is a click. Asymptotics: .This algorithm can be improved to
. To do this, you need to store a mask of vertices in the recursive search function, which we can still add. By supporting this mask, you can add only the "necessary" vertices, and then, at the end, you will not need to check the subgraph for what it is - a click. You can add a vertex for 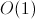, using the bitwise "and" of the current mask and the rows of the adjacency matrix of the added vertex.The solution to meet-in-the-middle.
1.1) We divide the graph G into 2 graphs G1 and G2 by N / 2 vertices. Find for
all clicks in each of them. Asymptotics: .Now it is necessary to find out for each click of the G1 graph the number of clicks of the G2 graph, such that their union is a click. Their sum is the final answer.
Since for a single clique K of the graph G1 there may be several suitable clicks in G2 , then using the same method as in the previous two examples will not work. But the only object for the clique K is the mask of the vertices of the graph G2 , which can still be added. We have a lot of time for pre-counting and this needs to be used: for each such mask in G2, you need to pre-calculate the answer, namely:
1.2) Using the dynamic programming method, for each mask of the vertices of the G2 graph, the number of clicks whose vertices are a subset of the selected mask is assumed. Number of states:
. Number of transitions: . Asymptotics: .Here is the Python translation:
for mask in range(1 << N): dp[mask] = 1 + sum([dp[mask & matrix[i]] for i in range(N) if ((mask & (1 << i)) > 0)]) 2) For each click of K (including an empty one) of the G1 graph, we add to the global answer the calculated number of clicks that can be added to K (including empty ones). Asymptotics:
.3) Profit:
.Conclusion
I hope I was able to lucidly explain the concept of meet-in-the-middle. If you have any questions - ask in the comments, I will try to answer. Thanks for attention.
Source: https://habr.com/ru/post/191266/
All Articles