Elliptical cryptography: practice

Hi% username%!

A couple of weeks ago I published the post Elliptic Cryptography: a theory in which I tried to describe the main aspects of using elliptic curves in cryptography. That my post carried exclusively fact-finding character, and did not provide any other work with the compiler, except contemplative. But what kind of theory without practice? In order to correct this omission, I, gathering my courage, rushed into battle with GOST, 10/34/2012, an EDS scheme on elliptic curves. If it is interesting to you to look that from all this it turned out, then welcome under kat.


')

Elliptic Curve Selection

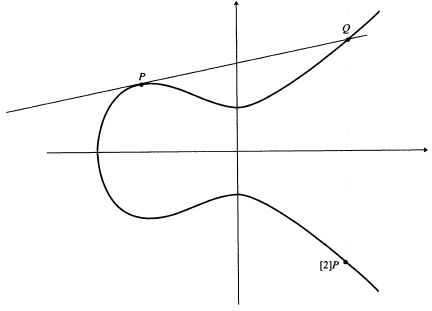
Let me remind you that in elliptical cryptography are used so-called. "Curves over a finite field". This means that the curves have a finite number of points. The number of points of such a curve is called the order of the curve . To use an elliptic curve in cryptography, you need to know its order. This is due at least to the fact that the crypto-resistance of the system depends on the order of the curve, which I wrote about in my previous opus.
This is where the complexity lies. The process of choosing a curve can be written as follows:

1. The choice of the parameters a and b, describing the equation of a straight line
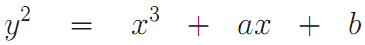
2. Counting the points of the selected curve;
3. Check whether the selected curve with a given number of points corresponds to a set of conditions.

So, the problem is that the calculation of the order of an elliptic curve is a very nontrivial task.

The most common method of calculating the number of points Shuf algorithm has a fairly large computational complexity . In addition, the algorithm uses very serious mathematical methods and is very difficult to understand.

There is another way, the so-called. complex multiplication method . The kind Habrachelovek grechnik has kindly shared information about this method in his post. Representation of numbers by the sum of two squares and elliptic curves . In short, this method makes it much more efficient to find curves with a given number of points. However, unlike the Shuf algorithm, which is universal, the complex multiplication method works only when certain conditions are met. This method is also not as simple as it may seem at first. More details about this can be for example here (thanks again for the link, grechnik ).

Fortunately, NIST, apparently in order to create backdoors to make life easier for developers, has compiled a list of elliptic curves with an already known number of points that are recommended for use in EDS schemes. Actually, I chose one of these curves for my experiments.

To describe the curve in the NIST standard, a set of 6 parameters D = (p, a, b, G, n, h) is used, where

p is a prime number, modulus of an elliptic curve;
a, b - set the equation of an elliptic curve ;
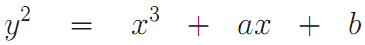G is a point of an elliptic curve of large order. This means that if you multiply a point by numbers smaller than the order of a point, each time you get completely different points;
n is the order of the point G;
h is a parameter called a cofactor. It is determined by the ratio of the total number of points on an elliptic curve to the order of the point G. This number should be as small as possible.

A couple of words about the parameters

Not really bothering with the choice, I decided to use the first NIST recommended curve, in which the value of the parameters described above is equal to:
p = 6277101735386680763835789423207666416083908700390324961279;
a = -3;
b = 2455155546008943817740293915197451784769108058161191238065;
x _G = 602046282375688656758213480587526111916698976636884684818 (the x-coordinate of the point G);
y _G = 174050332293622031404857552280219410364023488927386650641 (the y-coordinate of the point G);
n = 6277101735386680763835789423176059013767194773182842284081;
h = 1.

About the parameter p , I tell you in more detail. This number refers to the generalized Mersenne numbers , which means that it can be represented as the sum of the various powers of two. Specifically in our case, the number p can be written as
p = 2 ¹⁹² -2 ⁶⁴ -1.
All elliptic curves over a prime field recommended by NIST can be written in a similar way. Using such numbers allows you to speed up the multiplication operation modulo a large number. The essence of the method is reduced to the representation of the result of multiplication in the form of 32-bit machine words, the combination of which results in the desired product modulo a large number. You can read more about this, for example, here (thanks to datacompboy for the tip).

Another interesting point is related to the coordinates of the points. Often, in various kinds of specifications, the generator point G of an elliptic curve is specified in a compressed form. For example, in our case the point G can be set as follows:

G = 0x 03 188da80eb03090f67cbf20eb43a18800f4ff0afd82ff1012

The first byte stores the parity data of the y-coordinate. It can be equal to 2 (this means that the y-coordinate is even) or 3 (respectively, odd). The remaining bytes store the x-coordinate.
With this data we can restore the y-coordinate as follows.

We know that the point G belongs to an elliptic curve. Accordingly, for it is equal:



and we can calculate y like:

.

Since the result of calculating the square root modulo p is two numbers y and py , we choose the number whose parity coincides with the parity of the first byte of the compressed coordinate record G.

Signature generation

Before embarking on the implementation of the EDS algorithm itself, it is necessary to write a class for working with points of an elliptic curve. I wrote a little about mathematical laws and operations on elliptic curves in the last post, so I will not focus on this now.
Let me just say that to implement GOST 34.10, we need only three operations:

• Addition of two different points;
• Double point;
• Multiplication of a point by a number.

A little more details can be found, for example, on Wikipedia .

The implementation of the ECPoint class, which allows you to perform these actions, look under the spoiler.



To generate a digital signature, a large number d is used , which is the permanent secret key of the scheme, and should be known only to the signer.
To calculate the message signature M using the GOST algorithm, the following steps must be performed:

1. Calculate the message hash M: H = h (M). At this step, the Stribog hash function is used, which I already wrote about in Habré;
2. Calculate the integer α , the binary representation of which is H;
3. Define e = α mod n, if e = 0, set e = 1;
4. Generate a random number k satisfying the condition 0 <k <n;
5. Calculate the point of an elliptic curve C = k * G;
6. Determine r = x _C mod n, where x _C is the x-coordinate of point C. If r = 0, then return to step 4;
7. Calculate the value s = (rd + ke) mod n. If s = 0, then go back to step 4;
8. Return the value of r || s as a digital signature.

Let's write the SignGen function that implements all these actions:

  public string SignGen(byte[] h, BigInteger d) { BigInteger alpha = new BigInteger(h); BigInteger e = alpha % n; if (e == 0) e = 1; BigInteger k = new BigInteger(); ECPoint C=new ECPoint(); BigInteger r=new BigInteger(); BigInteger s = new BigInteger(); do { do { k.genRandomBits(n.bitCount(), new Random()); } while ((k < 0) || (k > n)); C = ECPoint.multiply(k, G); r = Cx % n; s = ((r * d) + (k * e)) % n; } while ((r == 0)||(s==0)); string Rvector = padding(r.ToHexString(),n.bitCount()/4); string Svector = padding(s.ToHexString(), n.bitCount() / 4); return Rvector + Svector; } 

In the given part of the code, the padding function complements the hexadecimal representations of the numbers r and s to the length of the module p, so that when checking the signature they can be parsed.

Signature verification

To verify the signature, a point Q is used that satisfies the equality Q = d * G. Point Q is the public key of the scheme and can be known to any verifier.
Signature verification process occurs according to the following algorithm:

1. According to the received signature, restore the numbers r and s. If the inequalities 0 <r <n and 0 <s <n are not met, then return “the signature is not true”;
2. Calculate the message hash M: H = h (M);
3. Calculate the integer α , the binary representation of which is H;
4. Define e = α mod n, if e = 0, set e = 1;
5. Calculate v = e ^-1 mod n;
6. Calculate the values ​​of z ₁ = s * v mod n and z ₂ = -r * v mod n;
7. Calculate the point of an elliptic curve C = z ₁ * G + z ₂ * Q;
8. Determine R = x _c mod n, where x _c is the x-coordinate of point C;
9. If R = r, then the signature is correct. Otherwise, the signature is not accepted.

To understand why this works, we write the signature verification process in the form of formulas:

As you can see, at the verification stage we get that same point C = k * G, as in the formation of the signature.

The SignVer function that performs the check:

  public bool SignVer(byte[] H, string sign, ECPoint Q) { string Rvector = sign.Substring(0, n.bitCount() / 4); string Svector = sign.Substring(n.bitCount() / 4, n.bitCount() / 4); BigInteger r = new BigInteger(Rvector, 16); BigInteger s = new BigInteger(Svector, 16); if ((r < 1) || (r > (n - 1)) || (s < 1) || (s > (n - 1))) return false; BigInteger alpha = new BigInteger(H); BigInteger e = alpha % n; if (e == 0) e = 1; BigInteger v = e.modInverse(n); BigInteger z1 = (s * v) % n; BigInteger z2 = n + ((-(r * v)) % n); this.G = GDecompression(); ECPoint A = ECPoint.multiply(z1, G); ECPoint B = ECPoint.multiply(z2, Q); ECPoint C = A + B; BigInteger R = Cx % n; if (R == r) return true; else return false; } 

The GDecompression () function unpacks points.

Fully DSGost class, which implements the signature and verification of messages using the GOST 34.10-2012 algorithm, you can look under the spoiler.


Example of working with the class:

  private void ECTest() { BigInteger p = new BigInteger("6277101735386680763835789423207666416083908700390324961279", 10); BigInteger a = new BigInteger("-3", 10); BigInteger b = new BigInteger("64210519e59c80e70fa7e9ab72243049feb8deecc146b9b1", 16); byte[] xG = FromHexStringToByte("03188da80eb03090f67cbf20eb43a18800f4ff0afd82ff1012"); BigInteger n = new BigInteger("ffffffffffffffffffffffff99def836146bc9b1b4d22831", 16); DSGost DS = new DSGost(p, a, b, n, xG); BigInteger d=DS.GenPrivateKey(192); ECPoint Q = DS.GenPublicKey(d); GOST hash = new GOST(256); byte[] H = hash.GetHash(Encoding.Default.GetBytes("Message")); string sign = DS.SignGen(H, d); bool result = DS.SignVer(H, sign, Q); } 

Conclusion

We considered the case when a cryptosystem is built on an elliptic curve over a residue field modulo a large prime number. However, one should not forget that the concept of elliptic cryptography includes much more than this single case. And when implementing cryptosystems on elliptic curves over fields of other types, it is necessary to take into account that the mathematical operations on these curves can differ significantly from those given in this post.

PS project sources are here .

Links

1. Reference to the standard GOST 34.10-2012;
2. Reference to the ECDSA standard with a list of recommended curves.
3. Standards for Efficient Cryptography, an extended list of recommended curves.