Analysis of all tasks and results of Yandex. Algorithm
Just a couple of hours ago, the open programming championship Yandex . Algorithm 2013 ended in St. Petersburg. The competitions consisted of several online rounds of 100 minutes each; over 3,000 programmers from 84 countries fought for the victory. According to the results of the three qualifying rounds, the top 25 reached the final.
The finalists had to solve six algorithmic problems in 100 minutes. First place was taken by the recent winner of ACM ICPC 2013 in the team of NRU ITMO Gennady Korotkevich (tourist), who scored the least of the penalty time. Second place went to a graduate of NRU ITMO Eugene Kapun (eatmore). Third place was taken by the representative of Taiwan, Shi Bisyun.
')
The preparation of tasks for the championship was attended by experts from several countries: Russia, Belarus, Poland and Japan. The main compilers of the tasks were the developers of the Minsk office of Yandex (they, like all employees of the company, were not allowed to participate in the competitions). We asked all authors to parse the tasks that they prepared for the participants of Yandex.Algorithm. By the way, all the tasks could not be solved by anyone, the best result - three solved problems - showed only three participants.
Author of the task and analysis: Jakub Pachocki, Warsaw U
Input file name : stdin
Output file name : stdout
Time limit : 8 seconds
Memory limit : 512 megabytes
Usually at team programming competitions, in addition to the full name of the university, the abbreviated is given. At one very prestigious competition, teams plan to spread out so that, of the two teams, the team with the lexicographically smallest shortened name sits closer to the sideboard. With this in mind, the coaches of each university strive to shorten the name of the university so that the result is lexicographically minimal.
Denote as a word a non-empty substring of the name of the university, which consists of letters, and neither the symbol immediately before this substring, nor the symbol immediately after it are letters. In the abbreviation of the name of the university, it is allowed to replace any suffix of a word with a dot (“.”).
Wherein:
It is allowed not to shorten the name of the university at all, leaving it unchanged.
When comparing names, all characters that are not Latin letters are deleted, all upper-case Latin letters are replaced with corresponding lower-case letters and the resulting strings are compared with each other.
The input file format. The first line of the input file contains the name of the university. The name may contain uppercase and lowercase Latin letters, spaces, commas (",") and hyphens ("-").
It is guaranteed that the line does not begin or end with a space and does not contain two consecutive spaces. The number of characters (including spaces) in the input file does not exceed 10 6 .
The format of the output file. Print the lexicographically smallest abbreviated university name. It is forbidden to change the capitalization of letters and the position of non-letter characters in comparison with the original name. If the lexicographically smallest
few cuts, output any.
Note. “Uni. Of W. ”is the lexicographically smallest abbreviation for“ University of Warsaw ”, since the string“ uniofw ”is lexicographically smaller than the lines corresponding to other options, for example,“ uow ”,“ uniofwa ”,“ universityofwarsaw ”.
Solutions to Problem A.
After parsing the input, the task is as follows:
Suppose that we have already found p k + 1 , ..., p n such that the string p k + 1 p k + 2 ... p n is lexicographically smallest. Note that this choice of p k + 1 , ..., p n is optimal for any choice of p 1 , ..., p k . This follows from the fact that if for two strings t and t ' t < t' is true, then wt < wt ' for any row w .
How to effectively find the optimal prefix p k for given p k + 1 , ...., p n ?
Let t : = p k + 1 p k + 2 ... p n . We need to find a non-empty prefix p of the string s k such that the string pt is lexicographically minimal.
There is an algorithm that allows you to effectively compare the pt and p't lines using a hash:
When using a randomized hash, the algorithm works in (log N ) with a very high probability.
In order to find p k , you need to hold | s k | - 1 such comparisons, which gives time(| s k | log N ) to calculate p k . Summing up all s k , we get the running time of the algorithm ( N log N ).
The authors of the task and analysis are Alexey Tolstikov and Roman Udovichenko.
Input file name : stdin
Output file name : stdout
Time limit : 2 seconds
Memory limit : 512 megabytes
Little Annie decided to study bit operations on numbers. Today she studied the operation “bitwise AND”. Bitwise AND is a binary operation, the action of which is equivalent to applying a logical AND to each pair of bits that are at the same positions in binary representations of operands (leading zeroes are valid in binary representation). In other words, if both corresponding bits of the operands are 1, the resulting binary bit is 1; if at least one bit of the pair is 0, the resulting binary bit is 0.
By a surprising coincidence, just today Anyuta’s parents brought two sets of numbers from work. Dad brought from work a set of A , consisting of P numbers, and a mother - a set of B , consisting of M numbers. All numbers in the sets were integer, non-negative, and not exceeding 65535. In addition, the numbers in the sets were numbered starting from 1.
Joyful Anyuta immediately began to apply the operation under study to the numbers from these sets. In order not to offend any of the parents, she applied bitwise AND to those pairs of numbers, one of which was from my father's set, and the other from my mother's.
While Annie was fascinated with calculations, it became interesting for parents how many ways their daughter could get a certain number X ? The number of different methods can be calculated as the number of different pairs (i, j) such that1 ≤ i ≤ P , 1 ≤ j ≤ M , A i AND B j = X. Since Anyuta's parents are no less inquisitive than their daughter, they want to find the desired number of ways not only for one number X , but immediately for K numbers X i . Help your parents!
The input file format. The first line contains three integers P , M and K (1 ≤ P , M , K ≤ 10 5 ), separated by spaces - the number of numbers in the set of dad, the number of numbers in the set of mom, and the number of numbers of interest to parents, respectively. The second line contains P numbers A i separated by spaces — the set of numbers that dad brought. The third line contains M numbers B i , separated by spaces — the set of numbers that mom brought. The fourth line contains K numbers X i separated by spaces - a set of numbers for which you need to count the required number of pairs. All numbers in sets A , B, and X are integers, non-negative, and do not exceed 65535.
The format of the output file. Output K lines containing one number each. The number in the i- th line should be equal to the number of ways to get the number X i by applying the bitwise AND operation to the numbers in sets A and B according to the rules described in the condition.
Examples
Solution of Problem B
Given two arrays A and B, consisting of non-negative integers up to 2 16 . An array of Q queries is also given, also containing numbers up to 2 16 . For each query k , it is necessary to say how many pairs ( i , j ) there are such that Ai AND Bj = Qk .
The number of elements in each array is up to 100k (although it is immediately clear that there are no more than 2 16 different ones, but all the same, the same must be processed, so let there be arrays up to 100k).
We will consider the answer immediately for all requests.
We introduce the following notation f ( x , S ) - the set of elements from the sequence S , which contain all the bits from x and possibly some more (that is, numbers such that x & y = x ).
Note that ifa ∈ f ( x , A ) and b ∈ f ( x , B ) , then ( a & b ) & x = x , i.e. a & b contains all the same bits as x , again, perhaps some more.
Let g ( x ) be the number of pairs of indices ( i , j ) such that A i & B j = x , it is easy to see that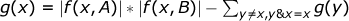
. Thus, from all possible pairs of indices we subtract those for which A i & B j > x .
Let B be the maximum number of bits in the numbers in the input. Then | f ( x , S ) | can be calculated in time O (| S | + 3 B ) for all x (using the method of enumerating all subsets of bits x ). The values of g ( x ) can be calculated in O (3 B ) time; however, in this case one should use enumeration of not all subsets of bits x , but all supersets.
The total time of the described solution is O ( P + M + K + 3 B ) ( B = 16).
Problem by jakubr (Jakub Radoszewski)
Input file name : stdin
Output file name : stdout
Time limit : 5 seconds
Memory limit : 512 megabytes
The hobby of the beekeeper Baytazar is the study of figures, which are formed in honeycombs with honey brought by bees. Each such figure is a connected set of hexagonal cells with side 1, inside of which there are no “holes”.
More formally, we call a figure without “holes” a subset of unit hexagons of a regular hexagonal grid such that any two unit hexagons belonging to it are connected by a path, all hexagons of which also belong to this set and any two neighboring hexagons (in the sense of this path) have a common side , and any two unit hexagons that do not belong to this subset are connected by a path, none of the cells of which belong to this set and any two adjacent (in the sense of this path) hexagonal Nicknames have a common side.
Baytazar wants to make a complete list of possible values of the perimeter and the number of cells in such patterns. He asked you to write a program that, using two given numbers n and p, ascertains whether there is a figure without “holes” consisting of n cells, the perimeter of which is equal to p .
For example, in the picture below, n = 4, and p = 18.
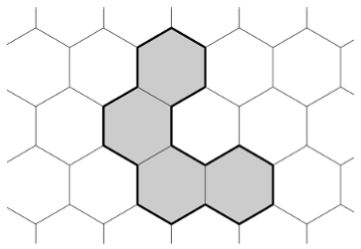
The input file format. The first line of input contains the number of test cases T (1 ≤ T ≤ 1000). Each of the following T lines defines a test case and contains two integers n and p (1 ≤ n , p ≤ 1000) - the required area and the perimeter of the figure.
The format of the output file . For each test case, in the order in which they appear in the input file, print the answer on a separate line. If there are no figures with the given parameters, output "NO". Otherwise, output a string of p characters composed of the letters “L” and “R”, specifying a detour along the perimeter of the figure (clockwise or against it), while “L” denotes a left turn, and “R” denotes a right turn.
If there are several correct answers, output any of them.
Solution of Problem C
The challenge is to build a polygon on a hexagonal grid,
consisting of n single cells and p sides, or make sure that a polygon with these parameters does not exist.
We fix the number of cells n and study the possible values of p such that a polygon with p sides exists. Obviously, p must be even.
It is also easy to see that p cannot be greater than 4 n + 2 (the perimeter of a polygon consisting of n cells running in a row and bordering on a side; let's call such a polygon a chain ).
On the other hand, from general considerations it is clear that the polygon of the minimum perimeter is a kind of large hexagon. Formally, its perimeter is given by the formula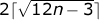
.
It turns out that these restrictions are not only necessary, but also sufficient.
The construction algorithm is as follows: we start with a chain consisting of n cells and having a maximum perimeter. Further, while the perimeter of our polygon is larger than p , we remove one cell from the “tail” of the polygon and add this cell to the “head”, completing the large hexagon layer by layer (see arrow 1 in the illustration).
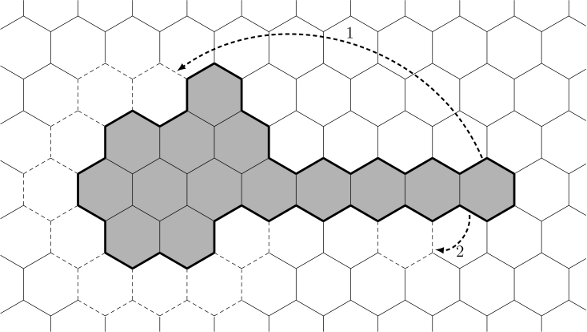
This move reduces the perimeter by 2, 4, or 6, so ultimately we will have to increase the perimeter by 2 or 4 by moving some cells (for example, moving the cell from the “tail” according to arrow 2 in the figure).
In some implementations, it will be necessary to separately analyze cases for small values of n , as well as cases when the perimeter is close to the minimum value for a given n .
The author of the task and analysis is Roman Udovichenko.
Input file name : stdin
Output file name : stdout
Time limit : 2 seconds
Memory limit : 512 megabytes
Little Anya loves to play with cubes. She has N positions, arranged in a row and numbered from 1 to N , in which she likes to build towers of cubes.
The tower is a few cubes lying one on another. Tower height is the number of cubes in it. The tower number corresponds to the position in which this tower is built.
Initially, all positions are empty. Every minute the following happens.
An example . Let the number of positions N = 6, and the heights of the towers be5 0 1 3 4 1 (numbering the positions from 1 to N from left to right). Then the next minute will happen next.
Change of tower heights within a minute in the example described above.
Once, Anyuta got tired of playing, and she decided to calculate how many cubes she would have in certain positions after a certain number of minutes. Since Annie is still small and there are so many cubes, she turned to you for help.
More formally, you need to answer Q requests of the form "how many will be in the sum of cubes in the towers with numbers from S i to F i inclusively after B i minutes". Requests are independent: in each request, it is assumed that initially all positions are empty, and after that i> B i minutes passes.
The input file format . The first line of the input contains two integers N and Q (2 ≤ N ≤ 10 18 , 1 ≤ Q ≤ 100 000) - the number of positions for the towers and the number of queries, respectively. Each of the following Q lines contains three integers S i , F i and B i (1 ≤ S i ≤ F i ≤ N , 1 ≤ B i ≤ 10 18 ) - the starting and ending positions for the request and the number of minutes elapsed after start pansing action.
The format of the output file . Print Q lines, one for each query. On each line print a single number - the answer to the query. Answer the queries in the order they appear in the input.
Examples
Solution of Problem D
First you need to understand how the cubes move in positions. Consider, for example, the case when N = 5.
In the first five minutes, the cubes will “crawl” one by one from position number 1 to position N , until one die appears in each position and the heights of the towers are equal to [1, 1, 1, 1, 1].
In the sixth minute, the die from the fourth position will move to the fifth, the cubes will move to the left one position to the right, and a new die will appear in position number 1: [1, 1, 1, 1, 2].
In the seventh minute, the cubes will only move from positions (3,2,1) to positions (4,3,2), respectively, and the heights will become [1, 1, 2, 2].
In the eighth minute, the cubes will move from positions 1-4: [1, 1, 1, 2, 3].
Continuing the simulation, we get:
After another 4 minutes the heights of the towers will become equal [1, 2, 3, 4, 5]. After another 5 minutes, the heights will be [2, 3, 4, 5, 6], after another 5 ~ - [3, 4, 5, 6, 7].
Thus, it is easy to notice the following pattern:
Considering the above, to answer each query, you must first calculate what kind of towers heights have now, and then apply some simple mathematical formulas related to arithmetic progressions.
The author of the task and work is Oleg Khristenko
Input file name : stdin
Output file name : stdout
Time limit : 2 seconds
Memory limit : 512 megabytes
Once Vasya was preparing for a maths Olympiad and fell asleep. Vasya dreamed of David Blaine saying the following:
“Now I will demonstrate mathematical magic. Look here: I write on the blackboard in a row N positive integers, greater than one and less than 2 63 . Some of these numbers are repeated: at least one of them is equal to some other number in the row. Below them, I write on the board a series of K < N positive integers, greater than one and less than 2 63 , some of which also repeat. Multiply the numbers in both sets ... the product of the numbers from the second set is exactly one more than the product of the numbers from the first set.
And now I remove some repetitions in the top row of numbers: the set of numbers present in the top row remains the same, but at least one element of the row I erase. I do the same with the bottom row ... again, not a single number of the series has disappeared at all, just some of the numbers have become smaller. Again, multiply the sets ... and see that the product of numbers from the second set is again exactly one more than the product of numbers from the first set. Magic!"
Vasya woke up, but could only remember N. Help him regain focus.
The input file format . The first line of the input file contains a single integer N (2 ≤ N ≤ 100) - the number of numbers in the set originally written by David Blaine.
The format of the output file . In the first line print the set originally written by David Blaine, in the second - the one that was written from the bottom, in the third and fourth - variants of these sets after David made the deletions. The numbers within each set must be sorted in non-decreasing order, must be greater than one and must not exceed 2 63 - 1.
If there are no sets satisfying the condition and constraints, output one word “Impossible” instead. If there are several such sets, output any of them.
Parsing task E
For N = 2, there is no solution (since K < N , one number is written out in the lower part, and it is impossible to cross out multiples). For N = 3, the solution is 8, 9, 2, 3 ({222}, {33}, {2}, {3}). It can be shown that this solution is unique. For N = 4, there is no solution. The proof is given at the end of the analysis.
We construct a solution for N ≥ 5.
For any N > 4, we take the numbers 2 (2 N -3 -1) and 2 N -1 (2 N -3 -1) as b and a .
Obviously, they are representable as the product of a certain number of twos and the number 2 N –3 –1, a is represented as a product of N factors, and a is divided by b . Check the conditions ona +1 and b +1 . a + 1 = (2 N -2 -2 ) + 1 = 2 N - 2 - 1 , and b + 1 = 2 N -2 (2 N -2 - 2) + 1 = (2 N -2 ) 2 - 2 * 2 N -2 + 1 = (2 N -2 - 1) 2 , that is, we obtain that a + 1 = ( b +1) 2 , and thus
we obtain sets of two and one numbers, respectively, satisfying the condition of the problem.
For 5 ≤ N ≤ 65, the answer thus generated is automatically suitable.
Further, we note that if the set q 1 , ..., q k is a solution to the problem for N = k, andq k = r 1 · r 2 , then the set q 1 , ..., q k-1 , r 1 , r 2 is the solution of the problem for N = k + 1 (we simply represent in the expansion of the number b the number { q k } as the product of the numbers r 1 and r 2 ). Similarly, the decomposition of one of the factors into the product of two smaller ones translates the pair ( a +1) , ( b +1) into the correct pair.
Therefore, we will try to decompose2 N -3 - 1 into factors not exceeding 2 63 - 1 , thereby obtaining from the same formula a solution for numbers from N + 1 to N + D - 1 , where D is the number of prime divisors of 2 N -3 - 1 . In the case of N > 65, it is required to decompose 2 N -2 - 1 into factors not exceeding 2 63 - 1 .
If N has a residue of 0 modulo 6, then N - 2 is divided by 2, N - 3 is divided by 3, and thus2 N -2 - 1 is represented as (2 ( N -2) / 2 - 1) (2 ( N -2) / 2 + 1) , and 2 N -3 - 1 - as (2 ( N -3) / 3 - 1) (2 (2 N -6) / 3 + 2 ( N -3) / 3 + 1) . It is easy to see that when N ≤ 95, both factors do not exceed 2 63 - 1 . And if so, then all their subsequent expansions also satisfy the requirements of the problem.
If N has a remainder of 5 modulo 6, thenN - 2 is divided by 3, and N - 3 - by 2, respectively, we use the same decomposition.
Thus, we start with N = 63 (2 60 -1 should be decomposed into a large number of factors, and2 61 -1 satisfies the requirement of the task), and then we iterate over all N not exceeding 96 and giving 0 or 5 when divided by 6, making the first decomposition of 2 N -3 - 1 into factors in the manner described in the previous paragraph (then expanding each of the factors “up to the stop”) and, also in accordance with this method, decomposing 2 N -2 - 1 into two factors. At the same time, the number of factors K in the set a + 1 will be four (the square of the number goes into the square of the product of two numbers), thus the condition K < N is satisfied. As a result of the search, we get that:
Thus, the algorithm finds solutions for all N ≤ 100.
Since N = 4, then, by the condition of the problem, a + 1 is decomposed into three factors or less. To be that cross out, at least two of them must be repeated. Also, by the condition of the problem, a is divided by b , that is,a = x b , x > 1 .
First, let us analyze all the variants of the set fora + 1 (and the corresponding set for b + 1 ):
In the case of 3a + 1 = uv 2 . Then b + 1 = uv ; x b + 1 = uv 2 , subtract, uv ( v - 1) = b ( x - 1) . Since uv and b are mutually simple, v - 1 is divisible by b , since v > 1 , v - 1 = y b ≥ b nobr>, v ≥ b + 1 . Since u > 1, then uv > v ≥ b + . Contradiction.
Since this argument does not use the fact thatu ≠ v , the case a + 1 = u 3 and b + 1 = u 2 is considered automatically.
Cases 1 ( u 2 , ~ u ) and 2 ( u 3 , ~ u ) remain . For them, consider the options for a set of four factors for a and a corresponding set for b .
I. a = x 2 y z , b = x y z ;
Ii. a = x 2 y 2 , b = x y 2 ;
Iii. a = x 3 y , b = x 2 y ;
Iv. a = x 4 , b = x 3 ;
V. a = x 2 y 2 , b = x y ;
Vi. a = x 4 , b = x 2 ;
VII. a = x 3 y , b = x y ;
Viii. a = x 4 , b = x .
Variants II – IV are obtained from variant I by substituting z = y , z = x andz = y = x, respectively. Similarly, option VI is a special case of option V.
In option I, replace y z with t .
1. x 2 t + 1 = v 2 , x t + 1 = v , whence x 2 t + 1 = x 2 t 2 + 2 x t + 1. Since all terms are positive and x 2 t 2 > x 2 t (since t > 1), then the right side is larger than the left.
2. x 2 t + 1 = v 3 , x t + 1 = v . By a similar substitution and opening of the brackets, we getx 2 t = x ^ 3 t 3 + 3 x 2 t 2 + 3 x t , all the terms are positive, x 2 t < x 3 t 3 .
Option V
1. x 2 y 2 + 1 = v 2 . Immediately does not happen for integers x , y , v > 1.
2. x 2 y 2 + 1 = v 3 , x y + 1 = v . When substituting and casting similar ones, we get that the sum( x y ) 3 + 2 ( x y ) 2 + 3 x y is 0, which is impossible for x , y > 1.
Option VII
1. x 3 y + 1 = v 2 , x y + 1 = v, rewrite asx 3 y + 1 = x 2 y 2 + 2 x y + 1 and then as x y ( x 2 - x y ) = 2 . It turns out that 2 is divided by x y , which for x > 1 and y > 1 cannot be.
2. x 3 y + 1 = v 3 , x y + 1 = v . We substitute, we get thatx 3 y = x 3 y 3 + ... (obviously positive numbers are indicated by ellipses), which is impossible for y > 1.
Option VIII
Let x 4 + 1 be divided by x + 1. Butx 4 + 1 = ( x + 1) ( x - 1) ( x 2 + 1) + 2 , that is, we obtain that 2 is divided by x + 1. Contradiction with the fact that x > 1.
We analyzed all cases and everywhere came to a contradiction, that is, with N = 4, there is no solution.
The author of the task and work is rng58 (Makoto Soejima)
Input file name : stdin
Output file name : stdout
Time limit : 2 seconds
Memory limit : 512 megabytes
The Hippo zebra has 10 18 stripes, numbered with consecutive integers from 0 to 10 18 - 1. At time 0, only the strip with the number5⋅ 10 17 is black, the rest are white. At time t ( t > 0), the color of the stripes satisfies the following rules:
10 9 + 7 t . , .
. t D (1 ≤ t ≤ 10 9 , 1 ≤ D ≤ 50), .
. — t 10 9 + 7
F
, . . :500 000 000 000 000 000+ x - x -.
: , t , . :
0, A .
Cycle:
The end of the cycle.
, t A .
f ( a 1 , a 2 ,..., a k ) — ,
A ={ a 1 , a 2 ,..., a k }.
{ a 1 , a 2 ,..., a k } , :
f ( a 1 , a 2 ,..., a k ) = 2 a 1 -1 + a 1 + a 2 -D-1 + a 2 + a 3 - D -1 +... .
,f ( a 1 , a 2 ,..., a k ) ( k ≤ T ).
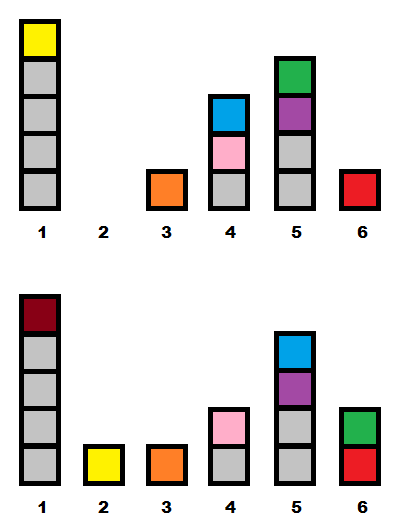
dp [ t ][ a ] ( t ≤ T, a ≤ D ) — f ( a 1 , a 2 ,..., a t-1 , a).
:
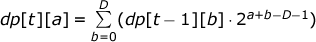
1 + dp [1][ D ] +… + dp [ T ][ D ], O(TD) .
, . v t —( dp [ t ][0],…, dp [ t ][ D ]) . , v t+1 = v t · A t ( A —
( D +1) × ( D +1)).
v 0 ⋅ ( A + A 2 +… + A T ) , .
— O( D 3 ⋅ log T ).
. ACM ICPC 2013 (Niyaz Nigmatullin) (mikhailOK), Facebook Hacker Cup, Google Code Jam . 2011, (Petr), - VK Cup 2012 (s-quark) .
, , , , , , . — Google, «» Facebook.
The finalists had to solve six algorithmic problems in 100 minutes. First place was taken by the recent winner of ACM ICPC 2013 in the team of NRU ITMO Gennady Korotkevich (tourist), who scored the least of the penalty time. Second place went to a graduate of NRU ITMO Eugene Kapun (eatmore). Third place was taken by the representative of Taiwan, Shi Bisyun.
')
The preparation of tasks for the championship was attended by experts from several countries: Russia, Belarus, Poland and Japan. The main compilers of the tasks were the developers of the Minsk office of Yandex (they, like all employees of the company, were not allowed to participate in the competitions). We asked all authors to parse the tasks that they prepared for the participants of Yandex.Algorithm. By the way, all the tasks could not be solved by anyone, the best result - three solved problems - showed only three participants.
Problem A. Reduce!
Author of the task and analysis: Jakub Pachocki, Warsaw U
Input file name : stdin
Output file name : stdout
Time limit : 8 seconds
Memory limit : 512 megabytes
Usually at team programming competitions, in addition to the full name of the university, the abbreviated is given. At one very prestigious competition, teams plan to spread out so that, of the two teams, the team with the lexicographically smallest shortened name sits closer to the sideboard. With this in mind, the coaches of each university strive to shorten the name of the university so that the result is lexicographically minimal.
Denote as a word a non-empty substring of the name of the university, which consists of letters, and neither the symbol immediately before this substring, nor the symbol immediately after it are letters. In the abbreviation of the name of the university, it is allowed to replace any suffix of a word with a dot (“.”).
Wherein:
- It is not allowed to replace the whole word with a dot.
- If the word remains unchanged (that is, an empty suffix is selected), the dot is not put.
It is allowed not to shorten the name of the university at all, leaving it unchanged.
When comparing names, all characters that are not Latin letters are deleted, all upper-case Latin letters are replaced with corresponding lower-case letters and the resulting strings are compared with each other.
The input file format. The first line of the input file contains the name of the university. The name may contain uppercase and lowercase Latin letters, spaces, commas (",") and hyphens ("-").
It is guaranteed that the line does not begin or end with a space and does not contain two consecutive spaces. The number of characters (including spaces) in the input file does not exceed 10 6 .
The format of the output file. Print the lexicographically smallest abbreviated university name. It is forbidden to change the capitalization of letters and the position of non-letter characters in comparison with the original name. If the lexicographically smallest
few cuts, output any.
| stdin | stdout |
| University of warsaw | Uni. of W |
| Saint Petersburg National Research University of Mechanics and Optics | Sain. Pe Na. Research Uni. of I., M. and O. |
| University of Illinois at Urbana-Champaign | Uni. of I. at U.-C |
| , Carnegie -, - MelloN -, -, - University- | , Ca .--, - MelloN -, -, - U.- |
| Udmurtian university | Udm. U. |
Note. “Uni. Of W. ”is the lexicographically smallest abbreviation for“ University of Warsaw ”, since the string“ uniofw ”is lexicographically smaller than the lines corresponding to other options, for example,“ uow ”,“ uniofwa ”,“ universityofwarsaw ”.
Solutions to Problem A.
After parsing the input, the task is as follows:
For n lines s 1 , ... s n of total length N, find their non-empty prefixes p 1 , ..., p n such that
p 1 p 2 ... p n
is lexicographically smallest.
Suppose that we have already found p k + 1 , ..., p n such that the string p k + 1 p k + 2 ... p n is lexicographically smallest. Note that this choice of p k + 1 , ..., p n is optimal for any choice of p 1 , ..., p k . This follows from the fact that if for two strings t and t ' t < t' is true, then wt < wt ' for any row w .
How to effectively find the optimal prefix p k for given p k + 1 , ...., p n ?
Let t : = p k + 1 p k + 2 ... p n . We need to find a non-empty prefix p of the string s k such that the string pt is lexicographically minimal.
There is an algorithm that allows you to effectively compare the pt and p't lines using a hash:
- using binary search we find the largest common prefix of the pt and p't strings ;
- compare the characters immediately following this prefix.
When using a randomized hash, the algorithm works in (log N ) with a very high probability.
In order to find p k , you need to hold | s k | - 1 such comparisons, which gives time
Problem B. Anyuta and “bitwise AND”
The authors of the task and analysis are Alexey Tolstikov and Roman Udovichenko.
Input file name : stdin
Output file name : stdout
Time limit : 2 seconds
Memory limit : 512 megabytes
Little Annie decided to study bit operations on numbers. Today she studied the operation “bitwise AND”. Bitwise AND is a binary operation, the action of which is equivalent to applying a logical AND to each pair of bits that are at the same positions in binary representations of operands (leading zeroes are valid in binary representation). In other words, if both corresponding bits of the operands are 1, the resulting binary bit is 1; if at least one bit of the pair is 0, the resulting binary bit is 0.
By a surprising coincidence, just today Anyuta’s parents brought two sets of numbers from work. Dad brought from work a set of A , consisting of P numbers, and a mother - a set of B , consisting of M numbers. All numbers in the sets were integer, non-negative, and not exceeding 65535. In addition, the numbers in the sets were numbered starting from 1.
Joyful Anyuta immediately began to apply the operation under study to the numbers from these sets. In order not to offend any of the parents, she applied bitwise AND to those pairs of numbers, one of which was from my father's set, and the other from my mother's.
While Annie was fascinated with calculations, it became interesting for parents how many ways their daughter could get a certain number X ? The number of different methods can be calculated as the number of different pairs (i, j) such that
The input file format. The first line contains three integers P , M and K (1 ≤ P , M , K ≤ 10 5 ), separated by spaces - the number of numbers in the set of dad, the number of numbers in the set of mom, and the number of numbers of interest to parents, respectively. The second line contains P numbers A i separated by spaces — the set of numbers that dad brought. The third line contains M numbers B i , separated by spaces — the set of numbers that mom brought. The fourth line contains K numbers X i separated by spaces - a set of numbers for which you need to count the required number of pairs. All numbers in sets A , B, and X are integers, non-negative, and do not exceed 65535.
The format of the output file. Output K lines containing one number each. The number in the i- th line should be equal to the number of ways to get the number X i by applying the bitwise AND operation to the numbers in sets A and B according to the rules described in the condition.
Examples
| stdin | stdout |
| 4 4 4 1 2 3 4 1 2 3 4 1 2 3 4 | 3 3 one one |
| 1 2 3 0 12 0 1 2 | 2 0 0 |
Solution of Problem B
Given two arrays A and B, consisting of non-negative integers up to 2 16 . An array of Q queries is also given, also containing numbers up to 2 16 . For each query k , it is necessary to say how many pairs ( i , j ) there are such that Ai AND Bj = Qk .
The number of elements in each array is up to 100k (although it is immediately clear that there are no more than 2 16 different ones, but all the same, the same must be processed, so let there be arrays up to 100k).
We will consider the answer immediately for all requests.
We introduce the following notation f ( x , S ) - the set of elements from the sequence S , which contain all the bits from x and possibly some more (that is, numbers such that x & y = x ).
Note that if
Let g ( x ) be the number of pairs of indices ( i , j ) such that A i & B j = x , it is easy to see that
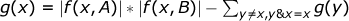. Thus, from all possible pairs of indices we subtract those for which A i & B j > x .Let B be the maximum number of bits in the numbers in the input. Then | f ( x , S ) | can be calculated in time O (| S | + 3 B ) for all x (using the method of enumerating all subsets of bits x ). The values of g ( x ) can be calculated in O (3 B ) time; however, in this case one should use enumeration of not all subsets of bits x , but all supersets.
The total time of the described solution is O ( P + M + K + 3 B ) ( B = 16).
Problem C. Bees
Problem by jakubr (Jakub Radoszewski)
Input file name : stdin
Output file name : stdout
Time limit : 5 seconds
Memory limit : 512 megabytes
The hobby of the beekeeper Baytazar is the study of figures, which are formed in honeycombs with honey brought by bees. Each such figure is a connected set of hexagonal cells with side 1, inside of which there are no “holes”.
More formally, we call a figure without “holes” a subset of unit hexagons of a regular hexagonal grid such that any two unit hexagons belonging to it are connected by a path, all hexagons of which also belong to this set and any two neighboring hexagons (in the sense of this path) have a common side , and any two unit hexagons that do not belong to this subset are connected by a path, none of the cells of which belong to this set and any two adjacent (in the sense of this path) hexagonal Nicknames have a common side.
Baytazar wants to make a complete list of possible values of the perimeter and the number of cells in such patterns. He asked you to write a program that, using two given numbers n and p, ascertains whether there is a figure without “holes” consisting of n cells, the perimeter of which is equal to p .
For example, in the picture below, n = 4, and p = 18.
The input file format. The first line of input contains the number of test cases T (1 ≤ T ≤ 1000). Each of the following T lines defines a test case and contains two integers n and p (1 ≤ n , p ≤ 1000) - the required area and the perimeter of the figure.
The format of the output file . For each test case, in the order in which they appear in the input file, print the answer on a separate line. If there are no figures with the given parameters, output "NO". Otherwise, output a string of p characters composed of the letters “L” and “R”, specifying a detour along the perimeter of the figure (clockwise or against it), while “L” denotes a left turn, and “R” denotes a right turn.
If there are several correct answers, output any of them.
| stdin | stdout |
| 3 4 18 3 18 3 12 | RLRRRRLRLRLRRRRLRL NO LRRRLRRRLRRR |
Solution of Problem C
The challenge is to build a polygon on a hexagonal grid,
consisting of n single cells and p sides, or make sure that a polygon with these parameters does not exist.
We fix the number of cells n and study the possible values of p such that a polygon with p sides exists. Obviously, p must be even.
It is also easy to see that p cannot be greater than 4 n + 2 (the perimeter of a polygon consisting of n cells running in a row and bordering on a side; let's call such a polygon a chain ).
On the other hand, from general considerations it is clear that the polygon of the minimum perimeter is a kind of large hexagon. Formally, its perimeter is given by the formula
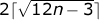.It turns out that these restrictions are not only necessary, but also sufficient.
The construction algorithm is as follows: we start with a chain consisting of n cells and having a maximum perimeter. Further, while the perimeter of our polygon is larger than p , we remove one cell from the “tail” of the polygon and add this cell to the “head”, completing the large hexagon layer by layer (see arrow 1 in the illustration).
This move reduces the perimeter by 2, 4, or 6, so ultimately we will have to increase the perimeter by 2 or 4 by moving some cells (for example, moving the cell from the “tail” according to arrow 2 in the figure).
In some implementations, it will be necessary to separately analyze cases for small values of n , as well as cases when the perimeter is close to the minimum value for a given n .
Problem D. Anyuta and cubes
The author of the task and analysis is Roman Udovichenko.
Input file name : stdin
Output file name : stdout
Time limit : 2 seconds
Memory limit : 512 megabytes
Little Anya loves to play with cubes. She has N positions, arranged in a row and numbered from 1 to N , in which she likes to build towers of cubes.
The tower is a few cubes lying one on another. Tower height is the number of cubes in it. The tower number corresponds to the position in which this tower is built.
Initially, all positions are empty. Every minute the following happens.
- Annie looks consistently at positions with numbers from N - 1 to 1.
- If at some position i there are cubes, and the height of the tower is greater than or equal to the height of the tower at position i + 1, Anyuta transfers one cube from the i -th position to ( i + 1) -th.
- After Annie has looked through all the positions, she adds one die to the tower in position number 1.
An example . Let the number of positions N = 6, and the heights of the towers be
- Anuta will look at position 5: the height of the tower in her is 4, while the height of the tower in the next position is 1. Anyuta will move one cube from position 5 to position 6. The heights of the towers will be
5 0 1 3 3 2 . - Anuta will look at position 4: the height of the tower in it is 3, and the height of the tower in the next position is 3. Annuta will transfer one cube from position 4 to position 5. The heights of the towers will be
5 0 1 2 4 2 . - From position 3 to position 4, Annie will not carry the cube, because the height of the tower at position 4 is greater than the height of the tower at position 3.
- From position 2 to position 3, Anjuta will not roll over the cube, because in position 2 there are no cubes.
- Finally, from position 1 to position 2, Annie will transfer one die. The heights of the towers will be equal to
4 1 1 2 4 2 . - After these actions, Annie will add one die to position number 1, and the heights of the towers will become equal to
5 1 1 2 4 2 .
Change of tower heights within a minute in the example described above.
Once, Anyuta got tired of playing, and she decided to calculate how many cubes she would have in certain positions after a certain number of minutes. Since Annie is still small and there are so many cubes, she turned to you for help.
More formally, you need to answer Q requests of the form "how many will be in the sum of cubes in the towers with numbers from S i to F i inclusively after B i minutes". Requests are independent: in each request, it is assumed that initially all positions are empty, and after that i> B i minutes passes.
The input file format . The first line of the input contains two integers N and Q (2 ≤ N ≤ 10 18 , 1 ≤ Q ≤ 100 000) - the number of positions for the towers and the number of queries, respectively. Each of the following Q lines contains three integers S i , F i and B i (1 ≤ S i ≤ F i ≤ N , 1 ≤ B i ≤ 10 18 ) - the starting and ending positions for the request and the number of minutes elapsed after start pansing action.
The format of the output file . Print Q lines, one for each query. On each line print a single number - the answer to the query. Answer the queries in the order they appear in the input.
Examples
| stdin | stdout |
| 10 3 1 1 1 1 10 100 10 10 11 | one 100 2 |
| 1 billion 2 1 1234 412412314 100000000000 999999999999 1000000000010 | 1234 900000000006 |
Solution of Problem D
First you need to understand how the cubes move in positions. Consider, for example, the case when N = 5.
In the first five minutes, the cubes will “crawl” one by one from position number 1 to position N , until one die appears in each position and the heights of the towers are equal to [1, 1, 1, 1, 1].
In the sixth minute, the die from the fourth position will move to the fifth, the cubes will move to the left one position to the right, and a new die will appear in position number 1: [1, 1, 1, 1, 2].
In the seventh minute, the cubes will only move from positions (3,2,1) to positions (4,3,2), respectively, and the heights will become [1, 1, 2, 2].
In the eighth minute, the cubes will move from positions 1-4: [1, 1, 1, 2, 3].
Continuing the simulation, we get:
- 9th minute: [1, 1, 2, 2, 3]
- 10th minute: [1, 1, 2, 3, 3]
- 11th minute: [1, 1, 2, 3, 4]
After another 4 minutes the heights of the towers will become equal [1, 2, 3, 4, 5]. After another 5 minutes, the heights will be [2, 3, 4, 5, 6], after another 5 ~ - [3, 4, 5, 6, 7].
Thus, it is easy to notice the following pattern:
- In the first N minutes, the heights of the towers are [1, ..., 1, 0, ..., 0];
- Further, the heights of the towers are either [1, ..., 1, 2, 3, ..., x ], or
[1, ..., 1, 2, 3, ..., k - 1, k , k , k + 1, ..., x ]; - Later
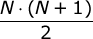minutes after the beginning of the height of the towers have the form [1, 2, 3, ..., N - 1, N ]; - After that, one cube is added to all towers in a circle.
Considering the above, to answer each query, you must first calculate what kind of towers heights have now, and then apply some simple mathematical formulas related to arithmetic progressions.
Problem E. Mathematical magic
The author of the task and work is Oleg Khristenko
Input file name : stdin
Output file name : stdout
Time limit : 2 seconds
Memory limit : 512 megabytes
Once Vasya was preparing for a maths Olympiad and fell asleep. Vasya dreamed of David Blaine saying the following:
“Now I will demonstrate mathematical magic. Look here: I write on the blackboard in a row N positive integers, greater than one and less than 2 63 . Some of these numbers are repeated: at least one of them is equal to some other number in the row. Below them, I write on the board a series of K < N positive integers, greater than one and less than 2 63 , some of which also repeat. Multiply the numbers in both sets ... the product of the numbers from the second set is exactly one more than the product of the numbers from the first set.
And now I remove some repetitions in the top row of numbers: the set of numbers present in the top row remains the same, but at least one element of the row I erase. I do the same with the bottom row ... again, not a single number of the series has disappeared at all, just some of the numbers have become smaller. Again, multiply the sets ... and see that the product of numbers from the second set is again exactly one more than the product of numbers from the first set. Magic!"
Vasya woke up, but could only remember N. Help him regain focus.
The input file format . The first line of the input file contains a single integer N (2 ≤ N ≤ 100) - the number of numbers in the set originally written by David Blaine.
The format of the output file . In the first line print the set originally written by David Blaine, in the second - the one that was written from the bottom, in the third and fourth - variants of these sets after David made the deletions. The numbers within each set must be sorted in non-decreasing order, must be greater than one and must not exceed 2 63 - 1.
If there are no sets satisfying the condition and constraints, output one word “Impossible” instead. If there are several such sets, output any of them.
| stdin | stdout |
| 2 | Impossible |
| 3 | 2 2 2 3 3 2 3 |
Parsing task E
For N = 2, there is no solution (since K < N , one number is written out in the lower part, and it is impossible to cross out multiples). For N = 3, the solution is 8, 9, 2, 3 ({222}, {33}, {2}, {3}). It can be shown that this solution is unique. For N = 4, there is no solution. The proof is given at the end of the analysis.
We construct a solution for N ≥ 5.
For any N > 4, we take the numbers 2 (2 N -3 -1) and 2 N -1 (2 N -3 -1) as b and a .
Obviously, they are representable as the product of a certain number of twos and the number 2 N –3 –1, a is represented as a product of N factors, and a is divided by b . Check the conditions on
we obtain sets of two and one numbers, respectively, satisfying the condition of the problem.
For 5 ≤ N ≤ 65, the answer thus generated is automatically suitable.
Further, we note that if the set q 1 , ..., q k is a solution to the problem for N = k, and
Therefore, we will try to decompose
If N has a residue of 0 modulo 6, then N - 2 is divided by 2, N - 3 is divided by 3, and thus
If N has a remainder of 5 modulo 6, then
Thus, we start with N = 63 (2 60 -1 should be decomposed into a large number of factors, and
- With N = 63, we get D = 13 factors, that is, we generate answers for
64 ≤ N ≤ 75. - For N = 71, we get D = 7 multipliers; we generate answers for N from 72 to 77 inclusive.
- When N = 77, we get D = 4 multipliers; we generate answers for N from 78 to 81 inclusive.
- When N = 78, we get D = 7 factors, we generate answers for N from 79 to 84 inclusive.
- When N = 83, we get D = 11 multipliers; we generate answers for N from 84 to 93 inclusive.
- When N = 90, we get D = 6 multipliers; we generate answers for N from 91 to 95 inclusive.
- When N = 95, we get D = 9 multipliers; we generate answers for N from 96 to 100 (even up to 104) inclusive.
Thus, the algorithm finds solutions for all N ≤ 100.
Proof of the impossibility of solving with N = 4
Since N = 4, then, by the condition of the problem, a + 1 is decomposed into three factors or less. To be that cross out, at least two of them must be repeated. Also, by the condition of the problem, a is divided by b , that is,
First, let us analyze all the variants of the set for
- u 2 , ~ u ;
- u 3 , ~ u ;
- uv 2 , uv ;
- u 3 , u 2 .
In the case of 3
Since this argument does not use the fact that
Cases 1 ( u 2 , ~ u ) and 2 ( u 3 , ~ u ) remain . For them, consider the options for a set of four factors for a and a corresponding set for b .
I. a = x 2 y z , b = x y z ;
Ii. a = x 2 y 2 , b = x y 2 ;
Iii. a = x 3 y , b = x 2 y ;
Iv. a = x 4 , b = x 3 ;
V. a = x 2 y 2 , b = x y ;
Vi. a = x 4 , b = x 2 ;
VII. a = x 3 y , b = x y ;
Viii. a = x 4 , b = x .
Variants II – IV are obtained from variant I by substituting z = y , z = x and
In option I, replace y z with t .
1. x 2 t + 1 = v 2 , x t + 1 = v , whence x 2 t + 1 = x 2 t 2 + 2 x t + 1. Since all terms are positive and x 2 t 2 > x 2 t (since t > 1), then the right side is larger than the left.
2. x 2 t + 1 = v 3 , x t + 1 = v . By a similar substitution and opening of the brackets, we get
Option V
1. x 2 y 2 + 1 = v 2 . Immediately does not happen for integers x , y , v > 1.
2. x 2 y 2 + 1 = v 3 , x y + 1 = v . When substituting and casting similar ones, we get that the sum
Option VII
1. x 3 y + 1 = v 2 , x y + 1 = v, rewrite as
2. x 3 y + 1 = v 3 , x y + 1 = v . We substitute, we get that
Option VIII
Let x 4 + 1 be divided by x + 1. But
We analyzed all cases and everywhere came to a contradiction, that is, with N = 4, there is no solution.
Problem F. Zebra Hippo and stripes
The author of the task and work is rng58 (Makoto Soejima)
Input file name : stdin
Output file name : stdout
Time limit : 2 seconds
Memory limit : 512 megabytes
The Hippo zebra has 10 18 stripes, numbered with consecutive integers from 0 to 10 18 - 1. At time 0, only the strip with the number
- x - t — 1 , t .
- t — 1 , , D x - , ( , y , 10 18 | x — y| ≤ D , y - t -1 ), t x -
. - x - t .
10 9 + 7 t . , .
. t D (1 ≤ t ≤ 10 9 , 1 ≤ D ≤ 50), .
. — t 10 9 + 7
| stdin | stdout |
| 5 1 | 36 |
| 2 3 | 1849 |
F
, . . :
: , t , . :
0, A .
Cycle:
- , .
- x — .
- d (0 < d ≤ D ) , ( x + d )- . d , .
- d A ( x + d )- .
The end of the cycle.
, t A .
f ( a 1 , a 2 ,..., a k ) — ,
A ={ a 1 , a 2 ,..., a k }.
{ a 1 , a 2 ,..., a k } , :
- 0-, a 1 -, ( a 1 + a 2 )- — .
- i ( a 1 +...+a i +1)- ( a 1 +...+a i -1 + D )- .
f ( a 1 , a 2 ,..., a k ) = 2 a 1 -1 + a 1 + a 2 -D-1 + a 2 + a 3 - D -1 +... .
,
dp [ t ][ a ] ( t ≤ T, a ≤ D ) — f ( a 1 , a 2 ,..., a t-1 , a).
:
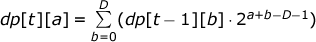
1 + dp [1][ D ] +… + dp [ T ][ D ], O(TD) .
, . v t —
— O( D 3 ⋅ log T ).
. ACM ICPC 2013 (Niyaz Nigmatullin) (mikhailOK), Facebook Hacker Cup, Google Code Jam . 2011, (Petr), - VK Cup 2012 (s-quark) .
, , , , , , . — Google, «» Facebook.
Source: https://habr.com/ru/post/191030/
All Articles