Greetings, friends.

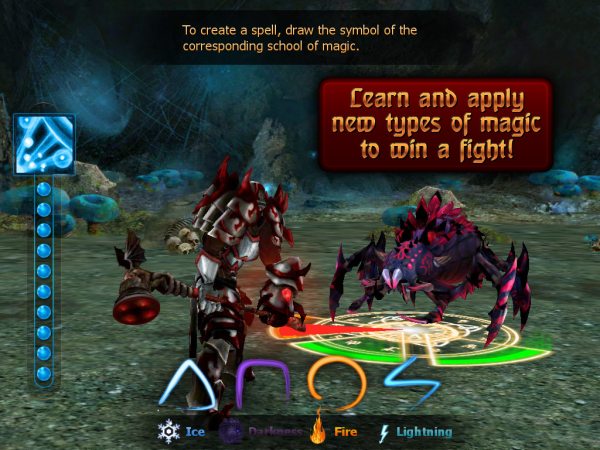
As you know, recently the technology of developing games for mobile platforms has been developing very rapidly. Games are written in a variety of engines and languages, we will not discuss in this article why a particular language / engine is better or worse (really?). Developers are trying to come up with new interesting and convenient game controls. As a player, I really like to use geometric elements in the game. For example, such as in the game Juggernaut for mobile devices.


')
I will try to tell you about the algorithm for determining drawn 2d shapes. I wrote my version of the engine in ActionScript 3.0. If desired (and the availability of basic knowledge of geometry) it can be implemented on any other.

So, we need to determine the percentage of similarity with the existing one using a hand-drawn figure:

Basic geometry

To implement the algorithm, we need the basic formulas of geometry on the plane.

[F1] Cut Length:

len = sqrt((x2-x1)^2 + (y2-y1)^2); 

[F2] Line direction and normal vectors:

 //     directX = x2-x1; directY = y2-y1; //      normaleX = -directY; normaleY = directX; 

[F3] Equation of a line on the plane Ax + By + C = 0

To get the coefficients A, B and C from the equation of a straight line, knowing the two points of this straight line, you can do this:

 A = -normaleX; B = -normaleY; C = -A*x1 - B*y1; 

[F4] The position of the point relative to the line.

We assume that a point lies above the line in the case that the formula Ax + By + C, when substituting the values, gives a value greater than zero. If the value is zero, then the point belongs to this line. Imagine that the first point of the line lies in the left part of the screen, and the second in the right, and so, all the points that lie above this line (at the top of the screen) will give a positive value when you substitute a straight line into the equation. It is very important to understand where the first (initial) point is, and where the second (final) is: if you have points p = {x, y} and q = {x, y} , and you calculate the direction (and normal vector) using the formula :

 directX = qx-px; directY = qy-py; 

, then the first (initial) point will be p , and the second (final) point will be q .

[F5] Belonging of a point to a segment

The point o belongs to the segment pq if it lies on a straight line passing through these points, and if it lies between two given points of the segment. The ownership algorithm is as follows:

- determine whether the point lies on the line ( [F4] )
- we find the lengths of the segments ( [F4] ) op and oq , if at least one of these values ​​is greater than the length of the segment pq , then the point o does not lie inside the segment pq

[F6] The intersection point of infinitely long straight lines

 // ,     l1 = {p1,p2}; l2 = {p1,p2}; // d = (l2.p2.y-l2.p1.y)*(l1.p2.x-l1.p1._x) - (l2.p2.x-l2.p1.x)*(l1.p2.y-l1.p1.y); a = (l2.p2.x-l2.p1.x)*(l1.p1.y-l2.p1._y) - (l2.p2.y-l2.p1.y)*(l1.p1.x-l2.p1.x) //   x0 = l1.p1.x + a*(l1.p2.x-l1.p1.x)/d y0 = l1.p1.y + a*(l1.p2.y-l1.p1.y)/d 

Note that if d = 0 , then the straight lines are parallel.

[F7] The intersection point of two segments. The point of intersection of the infinite line and the segment.

If the intersection of two finite segments or an infinite line and a final segment is checked, it is necessary to first determine the intersection point of two infinite lines ( [F6] ) and check whether this point belongs to all participating segments ( [F5] ).

Triangle - elementary polygon as the basis of everything

As you know the triangle is the easiest polygon. Many calculations of polygons are connected with triangles, therefore I will give several formulas for working with them.

[F8] Triangle Geometry Center

The center of a triangle (or Centroid ) is the arithmetic average of the coordinates of the points of the triangle. Determined by the formula:

 x0 = (a.x+b.x+cx)/3; y0 = (a.y+b.y+cy)/3; 

[F9] Triangle area

Knowing only the coordinates of the points of the triangle, its area can be determined by multiplying the lengths of the two sides by the sine of the angle between these sides.

[F10] Polygon on the plane

The polygon P on the plane is given by a set of vertices: v1, v2, ..., vn , where n is the number of vertices. The polygon has edges that are formed by connecting adjacent vertices: e1 = {v1, v2}, e2 = {v2, v3}, ..., en = {vn, v1} .

[F11] Polygon bounding box

The bounding box is given by the bounds = {x, y, width, height} object, where x and y are the minimum coordinates of the vertices of the polygon, and width and height are the difference between the maximum and minimum coordinates of the vertices.

[F12] Polygon Center

The center is usually understood as different entities, for example, the center of a system of points or the center of mass by area ... We will use the center of mass, which is calculated according to the following algorithm. It is necessary to split the polygon into triangles, no matter what, you can simply use the vertices in order. We find the sum of the products of the centers of triangles and their areas and divide this amount by the total area of ​​the polygon. The area of ​​the polygon is calculated as the sum of the areas of its triangles.

 //    var triangles:Array = ... ; //   var centerX:Number = 0; var centerY:Number = 0; //   var polygonSquare:Number = 0; // for (i=0; i<triangles.length; i++) { var triangle = triangles[i]; centerX += triangle.center.x*triangle.square; centerY += triangle.center.y*triangle.square; polygonSquare += triangle.square; } centerX /= polygonSquare; centerY /= polygonSquare; 

[F13] The position of the point relative to the polygon

The point is located inside the polygon in the event that this point is “below” with respect to all the edges when going around clockwise. The position of the point relative to the line can be determined by the formula F4 . If a point lies “above” with respect to all edges, then it lies outside the polygon.

[F14] The intersection of the infinite line and polygon

To determine the points of intersection of line l with polygon P, it is necessary to find all points of intersection of line l with all segments e1, e2 ... using the formula [F7] .

Determination of the similarity of figures

So what do we have at the entrance? We have a source drawing - a template polygon, defined by a set of vertices v1, v2, ..., vn, and there is a draw polygon consisting of a set of points that we got in the process of drawing. Before starting to compare them, the draw polygon must be “brought” to the polygon template. Those. It is necessary to apply a compression transformation (scale) and an offset (translate) so that the centers of the polygons coincide and the draw polygon has the most similar sizes of the bounding box with the template (bounds.width and bounds.height):



Algorithm for reducing polygons:

 //   var template = ... ; //   var draw = ... ; //    var scaleW:Number = template.bounds.width/draw.bounds.width; //    var scaleH:Number = template.bounds.height/draw.bounds.height; //    var scale:Number = (scaleW+scaleH)/2; //    draw.matrixScale(scale); // //   X var dx:Number = draw.centerWeight.x-template.centerWeight.x; //   Y var dy:Number = draw.centerWeight.y-template.centerWeight.y; //    draw.matrixTranslate(dx, dy); 

Note that centerWeight is the center of mass of the polygon.

To determine the similarity of the figures can be two algorithms, let's call them Radial and Dimensional . Let's break them down.

Radial algorithm

After you fit the drawn polygon to the template, we can start to compare them. The essence of the radial method is as follows. We let the ray out from the center and find the intersection points of this ray with the polygons. Find the distance between the intersection points and memorize it. Next, draw a new beam with a certain angle pitch, and also find the distance between the intersection points. If we add the distances between the intersection points at the end, we will get some value. The smaller this value, the closer the drawn figure to the pattern. An example can be seen in the image:



The more rays are released, the more accurate the check will be. You can also set the error, for example, how much the average length between the points of intersection of the beam with the polygons differs from the width / height (or the average arithmetic width and height) of the bounding rectangle of the polygon pattern. You can check the algorithm in the flash drive

Overall algorithm

The overall algorithm is to specify two bounding polygons within which all points of the drawn polygon must be located. Those. It is necessary to create two clones of the template and apply a transformation of compression to them: to one to the smaller side, to the other - to the big one. Next, we check all points that are inside a large polygon and outside a small one, after which we can determine the percentage of points that do not fall into this area. The percentage threshold value can be the level of accuracy of the drawn figure.



UPD: An example of a dimensional algorithm here .

Links

Libraries used for implementation in the ActionScript language: FPGeometry2d.swc and FPGeomControl.swc .