Brute force optimization
Disclaimer: for understanding this article, basic knowledge of graph theory is required, in particular, knowledge of depth -first search, breadth-first search, and the Bellman-Ford algorithm .
Surely you are faced with tasks that had to be solved by brute force. And if you were involved in Olympiad programming, then you definitely saw NP-complete tasks that no one can solve in polynomial time. Such tasks, for example, is finding the path of maximum length without self-intersections in the graph and many well-known game - sudoku , generalized by the size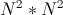 . Brute force is extremely long, because its operation time grows exponentially relative to the size of the input data. For example, the search time for the maximum path in a graph of 15 vertices is naively brute force, and at 20 it becomes very long.
. Brute force is extremely long, because its operation time grows exponentially relative to the size of the input data. For example, the search time for the maximum path in a graph of 15 vertices is naively brute force, and at 20 it becomes very long.
In this post I will tell you how to optimize the majority of searches, so that they begin to work orders of magnitude faster.
Consider a naive solution to the problem of finding a path of maximum length without self-intersections in the graph G.
')
Run a slightly modified deeper in depth . Namely, instead of checking whether we have visited a vertex, we are doing a verification that the vertex belongs to the current path. And now, if at each iteration we update the current global result, then as a result, this variable will contain the answer to the problem.
If you look into this solution a little deeper, you can see that the classic depth search was really launched, but on another graph, the state graph S. In this graph, the vertices are set as the mask of the vertices of the graph G belonging to the current path and the number of the last vertex. The edges are given by the presence of an edge in the graph G between the last vertices of the paths and the equality of the rest of the mask.
Most of the searches can be represented as a search in the state graph.
There are three types of searches:
1) Check existence.
2) Maximize / Minimize on a non-weighted graph.
3) Maximize / Minimize on a weighted graph.
To solve the first two problems using the naive method, we use depth search or width search, and for the third, the Bellman – Ford algorithm according to the state graph S.
And now the optimization itself.
No need to do the same thing several times. You can just remember the result, and when next time you need to do the same work, just take its result. This works on existence test tasks, and on the other two it sometimes partially works. There are two options: either the result of the state is encoded by him, or not. If yes, then memoization works fine. If not, memoization can help not to do work when the current response of the state is worse than it was once up to this point in the same state.
If the state graph S is small, then we are lucky - we can make a boolean array, otherwise, it is best to implement the memoization with a hash table.
This is usually not difficult to implement. We need to add 2 lines: at the beginning to check that we were not here yet, and at the end to write down what we were here.
The optimization is that we compare the estimate of the best answer achievable from this state with the current global result. This optimization works if we need to maximize or minimize something. In the case of an existence check, an assessment of the reachability of the result can be made. For example, in checking whether a graph is Hamiltonian, you can add a check on the reachability of all the vertices of the graph G , without passing through the vertices lying on the current path.
A good example for this optimization is finding the path of maximum length without self-intersections in the graph G. This task is NP-complete.
Suppose we are in some state s of the graph S. If we, anyway, do not succeed in improving the result, then we should return. Now we need to learn how to check it. For example, you can calculate the number of reachable vertices of the graph G from the last vertex of the state path s and add the length of the path already obtained, then the resulting number will be the upper limit of the maximum answer achievable from s . So, if it is less than the current result, then you can not run a search from this state.
If we abstract from a specific task, then we need to choose such a function.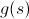 so that
so that 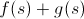 was an estimate of the answer achievable from s , where
was an estimate of the answer achievable from s , where 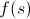 Is the current response of the state s .
Is the current response of the state s .
If the function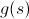 will reflect the reality well enough, this optimization can speed up the work of the algorithm by orders of magnitude.
will reflect the reality well enough, this optimization can speed up the work of the algorithm by orders of magnitude.
Clipping by answer is perhaps the most important optimization, because it is used by many other optimizations and methods.
Greed - is when we grab all the very, at first glance, good. That is, we go along the edge, which seemed to us more promising than the rest. The problem is that the answer that greed finds is not necessarily the best, but the better our estimate, the better the result. For the evaluation function you can take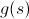 from the cut-off response.
from the cut-off response.
And now in order.
The cut-off response is triggered more often if there is a good answer. Then you can start the greedy algorithm first and get some answer. This will be a good start to cut off completely bad brute force branches.
Let's look at the job depth search. In the state s, we iterate over the edges in some random order and run from them further. So let's go through the edges in descending order of evaluation.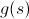 . To do this, simply sort them in the search in depth before going to the next state. Then the cut-off response will first receive higher-quality states. It is worth noting that in this form, the depth search at the very beginning will act as a greedy algorithm, which means it can not be run separately.
. To do this, simply sort them in the search in depth before going to the next state. Then the cut-off response will first receive higher-quality states. It is worth noting that in this form, the depth search at the very beginning will act as a greedy algorithm, which means it can not be run separately.
The Bellman-Ford algorithm is usually written like this:
And you can write it a little differently: how to search in width, but when checking whether we visited this state before, compare the current and memoized, and, if it is better, then cut off this branch of search.
Some pictures:


Red highlights the set of visited states of the graph S after some time of the search operation in depth and in width, respectively.
Both of these areas are very localized in one place. We need some kind of mechanism that will distribute the red area over the entire column S in order to quickly improve the answer, which will help to cut off the bad branches of the search.
If we solve the minimization problem, then the search actions in width look logical, but, unfortunately, it is unlikely to receive any answer for clipping.
And again greed came to us, but now in a slightly different way. Last time we sorted the edges and went over them all consistently, but this will weakly help us to search more globally than in the pictures above.
Everyone remembers that there is a number 1 and there is a number N , but many forget that there are also numbers between them. Greed is the choice of one edge, and the search in depth is the choice of N edges. Let's write a greedy depth search that will go through the first k edges.
If you use this method, then the search will bypass the much larger subtrees of the graph S.
The problem is that if you take too small k , the answer may be wrong, and if it is too large, then there may not be enough time. The solution is quite simple: you must select all possible k . That is, write an external cycle, sorting k from 1 to infinity, until time runs out, and in the body of the cycle, start searching for a solution.
It is worthwhile to understand here that since the number of scanned states of the graph S grows exponentially with respect to the growth of k , enumerating this variable from 1 to k -1 will not increase the asymptotic complexity. In the worst case, the operation time will increase by no more than a constant times, but in practice it will significantly decrease due to the cut-off for a good answer.
This method as if forces the search in depth to perform the wrong tasks that it usually performs.
The essence of the method is to create a global variable - the maximum depth to which the search in depth should go down. Just like with k, we start the outer loop at this depth.
Now the search in depth is more like a search in width, but with the difference that it immediately gets some answer for clipping.
This is also greed, but now for a wide search. From the name it is clear that we will limit the queue. To do this, we will again create a global variable - the size of the queue and iterate it from 2 to infinity. But we will not go through +1, but multiply by a constant, for example, by 2.
At some point, the queue size will exceed the selected maximum size and you have to throw someone overboard. To select, you must sort by some attribute. We will use, as always, the function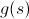 to compare states.
to compare states.
For best results, you need to write almost everything and almost immediately.
First, we start a depth search for some time with memoization, clipping by answer, sorting edges, and enumeration k , but without iterative deepening.
Next, we run a wide search with clipping by answer and limiting the queue size.
Search in depth is needed to find a good answer for clipping in the search in width, and search in width is needed to find the best answer already. This hodgepodge shows itself well in many brute-force tasks.
Search for a maximum path without self-intersections in the graph
Random graph: 18 vertices, 54 edges.
Working hours:
No optimizations ~ 4 sec.
Memoization, response cut-off ~ 0.2 ms.
Random graph: 30 vertices, 90 edges.
No optimizations> 1 hour (did not wait).
Memoization, response cut-off ~ 0.5 s.
Memoization, cut-off response, greed ~ 10 ms.
Introduction
Surely you are faced with tasks that had to be solved by brute force. And if you were involved in Olympiad programming, then you definitely saw NP-complete tasks that no one can solve in polynomial time. Such tasks, for example, is finding the path of maximum length without self-intersections in the graph and many well-known game - sudoku , generalized by the size
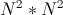 . Brute force is extremely long, because its operation time grows exponentially relative to the size of the input data. For example, the search time for the maximum path in a graph of 15 vertices is naively brute force, and at 20 it becomes very long.
. Brute force is extremely long, because its operation time grows exponentially relative to the size of the input data. For example, the search time for the maximum path in a graph of 15 vertices is naively brute force, and at 20 it becomes very long.In this post I will tell you how to optimize the majority of searches, so that they begin to work orders of magnitude faster.
More detail about brute force
Example
Consider a naive solution to the problem of finding a path of maximum length without self-intersections in the graph G.
')
Run a slightly modified deeper in depth . Namely, instead of checking whether we have visited a vertex, we are doing a verification that the vertex belongs to the current path. And now, if at each iteration we update the current global result, then as a result, this variable will contain the answer to the problem.
If you look into this solution a little deeper, you can see that the classic depth search was really launched, but on another graph, the state graph S. In this graph, the vertices are set as the mask of the vertices of the graph G belonging to the current path and the number of the last vertex. The edges are given by the presence of an edge in the graph G between the last vertices of the paths and the equality of the rest of the mask.
Most of the searches can be represented as a search in the state graph.
And what are we actually looking for?
There are three types of searches:
1) Check existence.
2) Maximize / Minimize on a non-weighted graph.
3) Maximize / Minimize on a weighted graph.
To solve the first two problems using the naive method, we use depth search or width search, and for the third, the Bellman – Ford algorithm according to the state graph S.
And now the optimization itself.
Optimization # 1: memoization , or laziness
No need to do the same thing several times. You can just remember the result, and when next time you need to do the same work, just take its result. This works on existence test tasks, and on the other two it sometimes partially works. There are two options: either the result of the state is encoded by him, or not. If yes, then memoization works fine. If not, memoization can help not to do work when the current response of the state is worse than it was once up to this point in the same state.
If the state graph S is small, then we are lucky - we can make a boolean array, otherwise, it is best to implement the memoization with a hash table.
This is usually not difficult to implement. We need to add 2 lines: at the beginning to check that we were not here yet, and at the end to write down what we were here.
Optimization # 2: cut-off response
The optimization is that we compare the estimate of the best answer achievable from this state with the current global result. This optimization works if we need to maximize or minimize something. In the case of an existence check, an assessment of the reachability of the result can be made. For example, in checking whether a graph is Hamiltonian, you can add a check on the reachability of all the vertices of the graph G , without passing through the vertices lying on the current path.
A good example for this optimization is finding the path of maximum length without self-intersections in the graph G. This task is NP-complete.
Suppose we are in some state s of the graph S. If we, anyway, do not succeed in improving the result, then we should return. Now we need to learn how to check it. For example, you can calculate the number of reachable vertices of the graph G from the last vertex of the state path s and add the length of the path already obtained, then the resulting number will be the upper limit of the maximum answer achievable from s . So, if it is less than the current result, then you can not run a search from this state.
If we abstract from a specific task, then we need to choose such a function.
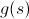 so that
so that 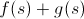 was an estimate of the answer achievable from s , where
was an estimate of the answer achievable from s , where 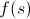 Is the current response of the state s .
Is the current response of the state s .If the function
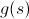 will reflect the reality well enough, this optimization can speed up the work of the algorithm by orders of magnitude.
will reflect the reality well enough, this optimization can speed up the work of the algorithm by orders of magnitude.Clipping by answer is perhaps the most important optimization, because it is used by many other optimizations and methods.
Optimization number 3: greed
Greed - is when we grab all the very, at first glance, good. That is, we go along the edge, which seemed to us more promising than the rest. The problem is that the answer that greed finds is not necessarily the best, but the better our estimate, the better the result. For the evaluation function you can take
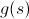 from the cut-off response.
from the cut-off response.And now in order.
The cut-off response is triggered more often if there is a good answer. Then you can start the greedy algorithm first and get some answer. This will be a good start to cut off completely bad brute force branches.
Let's look at the job depth search. In the state s, we iterate over the edges in some random order and run from them further. So let's go through the edges in descending order of evaluation.
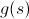 . To do this, simply sort them in the search in depth before going to the next state. Then the cut-off response will first receive higher-quality states. It is worth noting that in this form, the depth search at the very beginning will act as a greedy algorithm, which means it can not be run separately.
. To do this, simply sort them in the search in depth before going to the next state. Then the cut-off response will first receive higher-quality states. It is worth noting that in this form, the depth search at the very beginning will act as a greedy algorithm, which means it can not be run separately.A couple of words about weighted graphs
The Bellman-Ford algorithm is usually written like this:
for v in vertices: for e in edges: relaxation(e) And you can write it a little differently: how to search in width, but when checking whether we visited this state before, compare the current and memoized, and, if it is better, then cut off this branch of search.
What is “bad” search in depth and search in width
Some pictures:


Red highlights the set of visited states of the graph S after some time of the search operation in depth and in width, respectively.
Both of these areas are very localized in one place. We need some kind of mechanism that will distribute the red area over the entire column S in order to quickly improve the answer, which will help to cut off the bad branches of the search.
If we solve the minimization problem, then the search actions in width look logical, but, unfortunately, it is unlikely to receive any answer for clipping.
Mechanisms to select a search area
Greed
And again greed came to us, but now in a slightly different way. Last time we sorted the edges and went over them all consistently, but this will weakly help us to search more globally than in the pictures above.
Everyone remembers that there is a number 1 and there is a number N , but many forget that there are also numbers between them. Greed is the choice of one edge, and the search in depth is the choice of N edges. Let's write a greedy depth search that will go through the first k edges.
If you use this method, then the search will bypass the much larger subtrees of the graph S.
The problem is that if you take too small k , the answer may be wrong, and if it is too large, then there may not be enough time. The solution is quite simple: you must select all possible k . That is, write an external cycle, sorting k from 1 to infinity, until time runs out, and in the body of the cycle, start searching for a solution.
It is worthwhile to understand here that since the number of scanned states of the graph S grows exponentially with respect to the growth of k , enumerating this variable from 1 to k -1 will not increase the asymptotic complexity. In the worst case, the operation time will increase by no more than a constant times, but in practice it will significantly decrease due to the cut-off for a good answer.
Iterative deepening
This method as if forces the search in depth to perform the wrong tasks that it usually performs.
The essence of the method is to create a global variable - the maximum depth to which the search in depth should go down. Just like with k, we start the outer loop at this depth.
Now the search in depth is more like a search in width, but with the difference that it immediately gets some answer for clipping.
Limit the size of the search queue to the width
This is also greed, but now for a wide search. From the name it is clear that we will limit the queue. To do this, we will again create a global variable - the size of the queue and iterate it from 2 to infinity. But we will not go through +1, but multiply by a constant, for example, by 2.
At some point, the queue size will exceed the selected maximum size and you have to throw someone overboard. To select, you must sort by some attribute. We will use, as always, the function
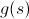 to compare states.
to compare states.What of all this to write now
For best results, you need to write almost everything and almost immediately.
First, we start a depth search for some time with memoization, clipping by answer, sorting edges, and enumeration k , but without iterative deepening.
Next, we run a wide search with clipping by answer and limiting the queue size.
Search in depth is needed to find a good answer for clipping in the search in width, and search in width is needed to find the best answer already. This hodgepodge shows itself well in many brute-force tasks.
Now a little practice
Search for a maximum path without self-intersections in the graph
Random graph: 18 vertices, 54 edges.
Working hours:
No optimizations ~ 4 sec.
Memoization, response cut-off ~ 0.2 ms.
Random graph: 30 vertices, 90 edges.
No optimizations> 1 hour (did not wait).
Memoization, response cut-off ~ 0.5 s.
Memoization, cut-off response, greed ~ 10 ms.
Source: https://habr.com/ru/post/190850/
All Articles