Ways to present dictionaries for automatic text processing
Automatic text analysis is almost always associated with work with dictionaries. They are used for morphological analysis, highlighting persons (dictionaries of personal names and surnames are needed) and organizations, as well as other objects.
In general, a dictionary is a set of records of the form {string, data associated with this string}.
For example, for morphological analysis, the dictionary consists of triples {word form, normal form, morphological characteristics}. When analyzing the word “soap” from the sentence “mom soap frame” one should be able to get the following analysis options:
')
At first glance, everything is simple. It is necessary to use a hash table and deal with the end. When the dictionary is small this solution is very simple and effective.
However, for example, the morphological dictionary of the Russian language contains about 5 million word forms. Turns out that:
This way of organizing data is uneconomical, because, firstly, words tend mostly regularly, and, secondly, in the case of the Russian language, within a single dictionary entry, subgroups of word forms can be distinguished, in which the form itself changes slightly or does not change at all .
For example, the word "wall":
It can be seen that only the ending changes, but the entire word must be stored in the hash table.
It is possible to separately store the bases (unchangeable parts) and endings, but in this case word verification becomes more complicated.
For clarity of examples, we will consider a simpler task, when for each word form in the analysis it is necessary to obtain only its morphological features. How to store the normal form will be described at the end.
Compared to hash tables, a more compact representation is the prefix tree (trie):
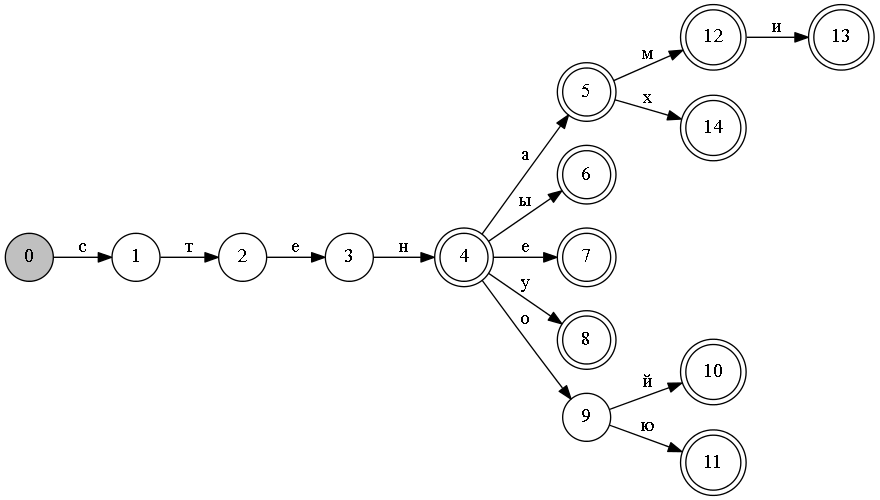
Important note - the figures will not show the sets of signs associated with each end node of the tree (or the state of the finite state machine). For example, in the figure, node 6, where we will get on the “wall” line, there will actually be 3 parses:
A prefix tree can be considered as a finite state machine.
In the machine there are three types of states:
In the following, the notation will be used:
I will give the basic algorithms for the prefix tree / finite automaton .:
The representation of a prefix tree as a finite state machine has important properties:
Such a special automaton is called a DAFSA (deterministic acyclic finite state automaton).
It is necessary to make one more important remark. For convenience of presentation and for practical use, we will assume that the state is described not only by the transition table, but also by the data on the final state. And we will assume that the state is final, if there is such data in it, and not - if they are absent.
Using prefix trees eliminates redundancy of prefixes. In fact, this means that the storage volume of the unchangeable part of the word is reduced. However, for example, in Russian, the end of a word changes mostly regularly.
For example, the words "arrow" and "wall" change in the same way:
WALL: units h: “wall” [im], “wall” [gender], “wall” [dates], “wall” [wine], “wall” [creator], “wall” [creator], “wall” [suggestion] ; mn h: "walls" [im], "walls" [genus], "walls" [dates], "walls" [wines], "walls" [creation], "walls" [pred].
BOOM: units h: “arrow” [them], “arrows” [gender], “arrow” [dates], “arrow” [wines], “arrow” [creative], “arrow” [creative], “arrow” [suggestion] ; mn h: “arrows” [them], “arrows” [gender], “arrows” [dates], “arrows” [wines], “arrows” [creation], “arrows” [pred].

It is seen that states 4 and 17, from which the endings begin, are equivalent for both words. Obviously, there will be many words with the same inflection rules in the dictionary. So you can significantly reduce the number of states.
Actually, in the theory of automata there is the concept of a minimal automaton — such an automaton that contains the minimum possible number of states but would be equivalent to this.
For example, for the above automaton, the minimum looks like this:

There are also algorithms for minimization of finite automata, but they all have a significant drawback - for their work, it is necessary to first build a non-minimized automaton.
Another less obvious drawback is that the constructed minimal automaton is not so easy to change. The simple procedure for adding a new word that is used for a prefix tree does not fit it.
For example, we built an automaton for the words "fox" and "box", and then minimized it.

If you add the word “foxes” to this machine without complete rebuilding, you get the following picture:

It turns out that in the place with “foxes” added “boxes”, which we did not add.
As a result, the scheme of using classical minimization algorithms is as follows: for any change in the dictionary, it is necessary:
If the dictionary is large, then these procedures can take considerable time and memory.
The solution to the difficulties with minimizing automata is presented in the work: Jan Daciuk; Bruce W. Watson; Stoyan Mihov; Richard E. Watson. "Incremental Construction of Minimal Acyclic Finite-State Automata" . It presents an algorithm for incremental minimization of deterministic acyclic finite automata. It allows changing the already constructed minimum automaton. As a result, it is not necessary to build a full automaton, and then minimize it.
Again, consider our machine WALL + BOOM:

An important concept of the algorithm is “row states” - this is a sequence of states, which is obtained by traversing an automaton on a given row.
For example, when crawling a string with an arrow, we get the following sequence of states [0, 1, 2, 14, 15, 4, 9, 10].
Another important concept of this algorithm is the number of transitions to a given state (confluence). If the number of transitions is more than one, then it is not safe to change this state. In the figure, this is state 4: it has 2 incoming arrows.
In addition, the algorithm assumes that there is a state registry that allows you to quickly get a state equal to this.
As a result, the algorithm for adding the word w looks like this:
Consider the simple case when the final state is a binary sign. Condition or final or not.
Machine for the string "fox".

It is seen that the machine is minimal, in the registry are all the states [0,1,2,3]
Add to it the word "box". Since they do not have a common prefix, we add the entire line as a suffix. As a result, we get:

You may notice that states 3 and 6 are equal. Replace 6 with 3:

Now you can see that they are equal to 2 and 5. Replace 5 with 2:

And now it is clear that they are equal to 1 and 4. Replace 4 with 1:

Add the line "foxes". When calculating the prefix, we found that the states [0, 1, 2, 3] are the prefix path.
In addition, they found that state 1 includes more than one transition. As a result, it is necessary to clone states 1, 2 and 3 along the path of bypassing the word “fox”, because if we simply add “foxes” to the previous automaton, the string “boxes” will be recognized, which we did not specify.

Now add the “boxes”:

When adding “boxes” the machine became smaller. This is, at first glance, an unexpected behavior, when, as new lines are added, the automaton actually decreases. There is also a reverse behavior - when the machine increases when a line is deleted.
For the correct operation of the algorithm, it is important to correctly implement the work with the registry. The state is deleted from the registry when any change occurs in the state transition table and the sign of finality.
In addition, in contrast to the usual set or table, in addition / deletion from the registry operates exactly this state, and the request is made for equal.
The presented algorithm is used in the AOT project and in the ETAP-3 system for organizing a quick morphological analysis. When using finite automata, an analysis speed of about 1-1.5 million words per second is achieved. In this case, the size of the machine without special tricks fits into 8 MB.
Previously described storing data strings as a sign of finality. Consider this approach in more detail.
The approach assumes that these strings are treated as some kind of atomic object. This in turn imposes restrictions on the efficiency of minimization of the automaton.
For example, the procedure for constructing a minimum automaton is meaningless for perfect hashing, when a unique number is associated with a string. Because in this case, each suffix will be unique, and accordingly, there will be no minimization, since each final state is unique.
For morphological analysis, sets of morphological characteristics can be used as associated data. This works well since there are few such sets relative to the total number of word forms. For example, in Russian, depending on the model adopted, the number of such sets is 500-900. A word forms 4-5 million
However, the efficiency of minimization comes to naught if, in addition to the characteristics, to maintain the full normal form. This is because the pair {normal form, morphological characteristics} is almost unique.
In the ETAP-3 system, this approach is used to store morphological information. The machine itself stores only sets of morphological signs. And to store the normal form, use the following trick. At the construction stage of the automaton, not one character, but two is used as an input symbol. For example, adding the word form “wall” (WALL in the instrumental case) will add the following sequence of pairs of characters: “c: C”, “t: T”, “e: E”, “n: H”, “o: A” , "Th: _".
All word forms of the words “wall” and “arrow” in such a machine will look like this:

This approach to writing normal forms has an important advantage. It allows you to work with morphology in two directions. It is possible to get its analysis by word form - analysis. And you can get all its word forms in normal form - synthesis.
The disadvantage of this approach is that, despite the fact that for a couple of signs the automaton is deterministic, it is no longer as such for the input and it is necessary to iterate through all transitions from this state. For example, the state m, in the figure above. It has several transitions on the sign of the word form "a".
Another way to store additional data was described in the original work. It involves changing the lines themselves, which are stored in the machine.
Proposed transaction scheme. Instead of the target line, an expanded line is written to the machine, which consists of the target line, the character of the beginning of the data (annotation symbol) and the data itself.
For example, in this case, the morphological characteristics can be written as follows: “wall | + ex + women + them, ...”, where '|' - an annotation symbol, and "+ cus", "+ wives", "+ them" - special data characters.
This approach is used in the AOT system. It actually stores two references as data: to the morphological characteristics and to the number of the inflection rule. As a result, the analysis can be obtained by the word form as its morphological features, and the initial form.
A feature of this approach is that the model of the automaton is somewhat complicated. The transition symbol is interpreted differently depending on whether it was before or after the annotation symbol.
Another feature is that for a line break is somewhat more complicated. First, the line is present in the automaton, if after its traversal we are in the state from which there is a transition by the annotation symbol. Secondly, the procedure for collecting all annotations after the annotation symbol is necessary. Third, an annotation decoding procedure is required.
To optimize the amount of memory, two representations of finite automata are used: one for constructing a minimum automaton, and the other for analysis. The difference between them is that the automaton for analysis does not imply changes and therefore can be more efficiently placed in memory.
The machine for analysis consists of three structures:
Machines are quite compact. For example, the AOT dictionary without any special tricks takes about 8Mb. The complete data of the system of morphological analysis, which include not only dictionary analysis, but also predictive analysis, the words fit into 16Mb.
The minimization algorithms themselves are implemented in my project on Github: github.com/kzn/fsa
In general, a dictionary is a set of records of the form {string, data associated with this string}.
For example, for morphological analysis, the dictionary consists of triples {word form, normal form, morphological characteristics}. When analyzing the word “soap” from the sentence “mom soap frame” one should be able to get the following analysis options:
| Normal form | Specifications |
|---|---|
| SOAP | S (noun), genus (genitive), ED (singular), MEDIUM (neuter gender), NEOD (inanimateness) |
| SOAP | S (noun), IM (nominative case), MN (plural), MEDIUM (neuter gender), NEOD (inanimateness) |
| SOAP | S (noun), VIN (accusative), MN (plural), MEDIUM (neuter gender), NEOD (inanimateness) |
| WASH | V (verb), PROSH (past tense), ED (singular), CONVERSION (indicative mood), WIFE (feminine), NESOV (imperfect form) |
')
Hash tables
At first glance, everything is simple. It is necessary to use a hash table and deal with the end. When the dictionary is small this solution is very simple and effective.
However, for example, the morphological dictionary of the Russian language contains about 5 million word forms. Turns out that:
- We must keep these 5 million word forms.
- For each word form there should be a link to a set of morphological characteristics.
- For each word form store its initial form
This way of organizing data is uneconomical, because, firstly, words tend mostly regularly, and, secondly, in the case of the Russian language, within a single dictionary entry, subgroups of word forms can be distinguished, in which the form itself changes slightly or does not change at all .
For example, the word "wall":
- units h: “walls a ” [them], “walls s ” [genus], “walls e ” [dates], “walls y ” [wines], “walls oh ” [creat], “walls oy ” [pieces], “Wall e ” [pred];
- mn h: “walls s ” [them], “walls” [genus], “walls am ” [dates], “walls s ” [wines], “walls am ” [creation], “walls ah ” [pred].
It can be seen that only the ending changes, but the entire word must be stored in the hash table.
It is possible to separately store the bases (unchangeable parts) and endings, but in this case word verification becomes more complicated.
From prefix tree to finite automata
For clarity of examples, we will consider a simpler task, when for each word form in the analysis it is necessary to obtain only its morphological features. How to store the normal form will be described at the end.
Compared to hash tables, a more compact representation is the prefix tree (trie):

Important note - the figures will not show the sets of signs associated with each end node of the tree (or the state of the finite state machine). For example, in the figure, node 6, where we will get on the “wall” line, there will actually be 3 parses:
- singular, genitive;
- plural, nominative .;
- plural, accusative.
A prefix tree can be considered as a finite state machine.
In the machine there are three types of states:
- The initial ones are those with which the work with an automatic machine begins. In a deterministic automaton, this state is one, but in a non-deterministic one there can be several. In the figures, this is the leftmost state with the number 0.
- Final - such states, the achievement of which means that there is such a word in the dictionary. They are denoted by a double circle.
- Simple states that are neither initial nor final
In the following, the notation will be used:
- line is denoted by w
- w [i] - i-th character of the given word (starting from 0).
- s [i] is the i-th node of the tree (or the state of the automaton), states are numbered with non-negative integers, we also assume that s [0] is the initial state.
- s [i] [j] - the transition from the state s [i] on the symbol j. We assume that if there is a transition, then such an expression will return a state number, if not, then it will return -1.
I will give the basic algorithms for the prefix tree / finite automaton .:
// // () int[] prefix(w) { int[] stateList; // stateList[0] = 0; int current = 0; for(int i = 0; i < length(w); i++) { int next = s[current][w[i]] // , if(next == -1) break; stateList[i+1] = next; } return stateList; } // // stateList void addSuffix(w, int[] stateList) { // int current = stateList[length(stateList) - 1]; for(int i = length(stateList) - 1; i < length(w); i++) { // int newState = addState(); // s[current][w[i]] = newState; current = newState; // stateList[i + 1] = current; } // s[current] setFinal(current); } // trie void add(w) { // int[] prefixStates = prefix(w); // addSuffix(w, prefixStates) } The representation of a prefix tree as a finite state machine has important properties:
- such an automaton is determined - from each state there can be no more than one transition on a certain symbol
- there are no cycles in it - with any method of bypassing the automaton, no state is visited more than once.
Such a special automaton is called a DAFSA (deterministic acyclic finite state automaton).
It is necessary to make one more important remark. For convenience of presentation and for practical use, we will assume that the state is described not only by the transition table, but also by the data on the final state. And we will assume that the state is final, if there is such data in it, and not - if they are absent.
Minimum state machines
Using prefix trees eliminates redundancy of prefixes. In fact, this means that the storage volume of the unchangeable part of the word is reduced. However, for example, in Russian, the end of a word changes mostly regularly.
For example, the words "arrow" and "wall" change in the same way:
WALL: units h: “wall” [im], “wall” [gender], “wall” [dates], “wall” [wine], “wall” [creator], “wall” [creator], “wall” [suggestion] ; mn h: "walls" [im], "walls" [genus], "walls" [dates], "walls" [wines], "walls" [creation], "walls" [pred].
BOOM: units h: “arrow” [them], “arrows” [gender], “arrow” [dates], “arrow” [wines], “arrow” [creative], “arrow” [creative], “arrow” [suggestion] ; mn h: “arrows” [them], “arrows” [gender], “arrows” [dates], “arrows” [wines], “arrows” [creation], “arrows” [pred].

It is seen that states 4 and 17, from which the endings begin, are equivalent for both words. Obviously, there will be many words with the same inflection rules in the dictionary. So you can significantly reduce the number of states.
Actually, in the theory of automata there is the concept of a minimal automaton — such an automaton that contains the minimum possible number of states but would be equivalent to this.
For example, for the above automaton, the minimum looks like this:
There are also algorithms for minimization of finite automata, but they all have a significant drawback - for their work, it is necessary to first build a non-minimized automaton.
Another less obvious drawback is that the constructed minimal automaton is not so easy to change. The simple procedure for adding a new word that is used for a prefix tree does not fit it.
For example, we built an automaton for the words "fox" and "box", and then minimized it.

If you add the word “foxes” to this machine without complete rebuilding, you get the following picture:

It turns out that in the place with “foxes” added “boxes”, which we did not add.
As a result, the scheme of using classical minimization algorithms is as follows: for any change in the dictionary, it is necessary:
- Build a prefix tree (or store)
- Minimize machine
If the dictionary is large, then these procedures can take considerable time and memory.
Incremental minimization of deterministic acyclic finite automata
The solution to the difficulties with minimizing automata is presented in the work: Jan Daciuk; Bruce W. Watson; Stoyan Mihov; Richard E. Watson. "Incremental Construction of Minimal Acyclic Finite-State Automata" . It presents an algorithm for incremental minimization of deterministic acyclic finite automata. It allows changing the already constructed minimum automaton. As a result, it is not necessary to build a full automaton, and then minimize it.
Again, consider our machine WALL + BOOM:
An important concept of the algorithm is “row states” - this is a sequence of states, which is obtained by traversing an automaton on a given row.
For example, when crawling a string with an arrow, we get the following sequence of states [0, 1, 2, 14, 15, 4, 9, 10].
Another important concept of this algorithm is the number of transitions to a given state (confluence). If the number of transitions is more than one, then it is not safe to change this state. In the figure, this is state 4: it has 2 incoming arrows.
In addition, the algorithm assumes that there is a state registry that allows you to quickly get a state equal to this.
As a result, the algorithm for adding the word w looks like this:
void addMinWord(w) { // w int[] stateList = commonPrefix(w); // int confIdx = findConfluence(stateList); // if(confIdx > -1) { int idx = confIdx; while(idx < length(stateList)) { int prev = stateList[idx - 1]; int cloned = cloneState(stateList[idx]); stateList[idx] = cloned; // // s[prev][w[idx - 1]] = cloned; idx++; confIdx++; } } // addSuffix(w, stateList); // , . // , replaceOrRegister(w, nodeList); } void replaceOrRegister(w, int[] stateList) { int stateIdx = length(stateList) - 1; int wordIdx = length(w) - 1; // while(stateIdx > 0) { int state = stateList[stateIdx]; // , state int regState = registerGet(state); if(regState == state) { // state , continue; } else if(regState == -1) { // , registerAdd(state); } else { // , , state int in = w[wordIdx]; // s[stateList[stateIdx - 1]][in] = regState; // stateList[stateIdx] = regState; // removeState(state); } wordIdx--; stateIdx--; } } Illustration of the algorithm
Consider the simple case when the final state is a binary sign. Condition or final or not.
Machine for the string "fox".

It is seen that the machine is minimal, in the registry are all the states [0,1,2,3]
Add to it the word "box". Since they do not have a common prefix, we add the entire line as a suffix. As a result, we get:

You may notice that states 3 and 6 are equal. Replace 6 with 3:

Now you can see that they are equal to 2 and 5. Replace 5 with 2:

And now it is clear that they are equal to 1 and 4. Replace 4 with 1:

Add the line "foxes". When calculating the prefix, we found that the states [0, 1, 2, 3] are the prefix path.
In addition, they found that state 1 includes more than one transition. As a result, it is necessary to clone states 1, 2 and 3 along the path of bypassing the word “fox”, because if we simply add “foxes” to the previous automaton, the string “boxes” will be recognized, which we did not specify.

Now add the “boxes”:

When adding “boxes” the machine became smaller. This is, at first glance, an unexpected behavior, when, as new lines are added, the automaton actually decreases. There is also a reverse behavior - when the machine increases when a line is deleted.
For the correct operation of the algorithm, it is important to correctly implement the work with the registry. The state is deleted from the registry when any change occurs in the state transition table and the sign of finality.
In addition, in contrast to the usual set or table, in addition / deletion from the registry operates exactly this state, and the request is made for equal.
Practical use
The presented algorithm is used in the AOT project and in the ETAP-3 system for organizing a quick morphological analysis. When using finite automata, an analysis speed of about 1-1.5 million words per second is achieved. In this case, the size of the machine without special tricks fits into 8 MB.
Previously described storing data strings as a sign of finality. Consider this approach in more detail.
Data storage in the state of the machine
The approach assumes that these strings are treated as some kind of atomic object. This in turn imposes restrictions on the efficiency of minimization of the automaton.
For example, the procedure for constructing a minimum automaton is meaningless for perfect hashing, when a unique number is associated with a string. Because in this case, each suffix will be unique, and accordingly, there will be no minimization, since each final state is unique.
For morphological analysis, sets of morphological characteristics can be used as associated data. This works well since there are few such sets relative to the total number of word forms. For example, in Russian, depending on the model adopted, the number of such sets is 500-900. A word forms 4-5 million
However, the efficiency of minimization comes to naught if, in addition to the characteristics, to maintain the full normal form. This is because the pair {normal form, morphological characteristics} is almost unique.
In the ETAP-3 system, this approach is used to store morphological information. The machine itself stores only sets of morphological signs. And to store the normal form, use the following trick. At the construction stage of the automaton, not one character, but two is used as an input symbol. For example, adding the word form “wall” (WALL in the instrumental case) will add the following sequence of pairs of characters: “c: C”, “t: T”, “e: E”, “n: H”, “o: A” , "Th: _".
All word forms of the words “wall” and “arrow” in such a machine will look like this:

This approach to writing normal forms has an important advantage. It allows you to work with morphology in two directions. It is possible to get its analysis by word form - analysis. And you can get all its word forms in normal form - synthesis.
The disadvantage of this approach is that, despite the fact that for a couple of signs the automaton is deterministic, it is no longer as such for the input and it is necessary to iterate through all transitions from this state. For example, the state m, in the figure above. It has several transitions on the sign of the word form "a".
Data storage in transitions. Using annotations
Another way to store additional data was described in the original work. It involves changing the lines themselves, which are stored in the machine.
Proposed transaction scheme. Instead of the target line, an expanded line is written to the machine, which consists of the target line, the character of the beginning of the data (annotation symbol) and the data itself.
For example, in this case, the morphological characteristics can be written as follows: “wall | + ex + women + them, ...”, where '|' - an annotation symbol, and "+ cus", "+ wives", "+ them" - special data characters.
This approach is used in the AOT system. It actually stores two references as data: to the morphological characteristics and to the number of the inflection rule. As a result, the analysis can be obtained by the word form as its morphological features, and the initial form.
A feature of this approach is that the model of the automaton is somewhat complicated. The transition symbol is interpreted differently depending on whether it was before or after the annotation symbol.
Another feature is that for a line break is somewhat more complicated. First, the line is present in the automaton, if after its traversal we are in the state from which there is a transition by the annotation symbol. Secondly, the procedure for collecting all annotations after the annotation symbol is necessary. Third, an annotation decoding procedure is required.
Memory optimization
To optimize the amount of memory, two representations of finite automata are used: one for constructing a minimum automaton, and the other for analysis. The difference between them is that the automaton for analysis does not imply changes and therefore can be more efficiently placed in memory.
The machine for analysis consists of three structures:
- transition table - pairs of integers {transition symbol, target state}
- indexes of the beginning and end of the state transition range
- final state data table
Machines are quite compact. For example, the AOT dictionary without any special tricks takes about 8Mb. The complete data of the system of morphological analysis, which include not only dictionary analysis, but also predictive analysis, the words fit into 16Mb.
The minimization algorithms themselves are implemented in my project on Github: github.com/kzn/fsa
Source: https://habr.com/ru/post/190694/
All Articles