Data structures, PHP. Part two
I continue to combine business with pleasure and translate. Today we’ll talk about heaps and graphs. As usual, the material is more suitable for beginners - most of the information, if not all, has already been covered in some way or another.
At the end of the last article, trees were touched upon, so let's start with a heap, since there are common roots between the heap and the trees. Then we go to the graphs and implement the Dijkstra algorithm.
UPD : Added performance comparison
A heap is a special, tree-like structure that has one property — any parent node is always greater or equal to its descendants. Thus, if this condition is met, the root element of the heap will always be maximal. This option is called the maximum (full) heap or maxheap. The heap where the root element is minimal and each parent node is less than or equal to its descendants is the minimal heap or minheap.
')
Binary heap (maxheap) can be represented as follows:
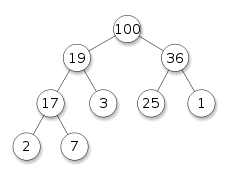
It is binary because each parent has two children.
It should be noted that heaps, though implemented as binary trees, but they do not have such a thing as ordering and there is no specific order for traversing. A heap is a variant of a table structure, therefore the following basic operations are applicable to it:
Since the operations of receiving and deleting elements are combined in one extraction operation, we will consider it for the beginning.
The rule for removing an element from a heap is that only the root element can be deleted. Suppose we have removed the root element from the example above (100). After deletion, we will be left with two separate heaps and we need to somehow rebuild it all into one separate heap. It is easiest to do this by moving the last node to the root, but in this case such a heap will not be suitable for the main condition. Such a pile is called semiheap:
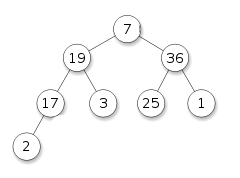
Now it is necessary to make a normal pile out of half a heap. One of the possible solutions to this problem is to lower the new root downwards, simultaneously comparing the root element with its descendants and changing its places with the maximum descendant. Thus, we will return the maximum element to the root, while lowering the minimum to the maximum.
We can implement maxheap as an array. A node in a binary tree cannot have more than two children, so for any number of nodes n a binary heap will have 2n + 1 nodes.
We implement a bunch as follows:
Insertion is the opposite, the exact opposite of extraction: we insert an element down the heap and raise it until it is possible and the main condition is met. Since we know that a full binary tree contains an n / 2 + 1 node, we can bypass the heap using a simple binary search.
Let's see what we did and try to insert several values into the heap:
If we try to derive all this, we get the following:
As you can see, the order is not observed, and in general this is somewhat different than what we expected. However, if we in turn take elements from the heap, then everything will be fine:
Fortunately, we already have ready-made implementations of SplHeap, SplMaxHeap and SplMinHeap. All we need to do is just to inherit them and override the comparison method, like this:
This method will perform any comparison of two nodes, and in the case of SplMaxHeap, it returns a positive number if $ item1 is greater than $ item2, 0 if they are equal to each other, and negative if $ item2 is greater than $ item1. If we inherit SplMinHeap, then it will return a positive number if $ item1 is less than $ item2.
It is not recommended to put several identical elements in a heap, since their position will be difficult to determine
A priority queue is a special abstract data type that behaves like a queue, but is implemented as a heap. Regarding the SplPriorityQueue this will be maxheap The priority queue has quite a few real-world applications, for example, a ticket system or help desk.
As in the case of SplHeap, you only need to inherit the SplPriorityQueue and override the comparison method:
The main difference in SplPriorityQueue is that when inserting, in addition to the element value, the priority of this element is also expected. The insert operation uses priority to sift through the heap based on the result that your comparator returns.
Let's check the work of the priority queue, set the numbers as numbers:
What ultimately will give us the following:
In this case, our elements go in descending order of priority - from the highest to the lowest (lower value means higher priority). You can change the order in which items are returned by simply changing the comparison method so that it returns a positive number if $ p1 is greater than $ p2.
By default, only the value of the element is retrieved. If you want to get only the values of the priority, or the values and their priority, you need to set the appropriate flag to extract:
Behind the graphs there are quite a few real-world applications — network optimization, routing, or analysis of social networks. Google PageRank, recommendations from Amazon are some examples of their use. In this part of the article I will try to explain two tasks in which they are used - problems finding a short cut and the least number of stops.
A graph is a mathematical construct used to represent relationships between key-value pairs. A graph consists of a set of vertices (nodes) and an arbitrary number of connections between nodes connecting them to each other. These links can be directional (oriented) and non-directional. A directional link is a link between two nodes and the link A → B is not the same as B → A. The non-directional link has no direction, so the AB and BA links are identical. Based on these rules, we can say that trees are one of the undirected graphs, where each vertex is connected to one of the nodes by a simple link.
Counts can also have weight. A weighted graph, or a network, is a graph whose weight is indicated for each connection (the “price” of the transition from node A to node B). Such constructions are widely used to determine the most optimal path, or the most “cheap” path between two points. Laying the way in GoogleMap is carried out with the help of a weighted graph.
The general application of graph theory is used when searching for the minimum number of stops between two nodes. As for trees, here the graphs help in traversing the tree in one of two directions - in depth or in width. Since last time we considered the search in depth, now let's take a look at another method.
Imagine the following graph:

For simplicity, we agree that this graph is undirected. The task is to find the minimum number of stops between any two nodes. When searching in width, we start from the root (well, or from another node, which we denote as root) and go down the tree level by level. To implement this, we need a queue to organize a list of nodes that we have not yet walked around in order to return to it and process it at each level. The general algorithm is as follows:
But how do we know which nodes are adjacent or unvisited without resorting to traversing the graph? This brings us to the question of how graphs can be modeled.
Usually, graphs are represented in two ways - a table or a matrix, where neighboring nodes are described.
Here is how it looks for the first example:


In the matrix, at the intersection of nodes is put "1", if the nodes are neighbors.
The list is useful if most of the vertices do not have connections between themselves, the matrix provides a faster search. In the end, the type of representation of the graph depends on what operations with the graph will be performed. We will use the list.
And write our search in width:
By running this example we get the following:
If we used the stack instead of the queue, then the round would be in depth.
Another common problem is finding the optimal path between any two nodes. Earlier, I already spoke about building a route in GoogleMaps as an example of solving this problem. Alternatively, this task can be applied to routing, traffic management, and so on.
One of the famous algorithms aimed at solving this problem was invented in 1959 by a 29-year-old scientist named Edsger Wibe Dijkstra . You can learn more about the algorithm in Wikipedia or look at it at the splitface . In general, Dijkstra’s solution comes down to checking each connection between all possible pairs of nodes, starting from the starting node, and maintaining an updated set of nodes with the shortest distance until the target node is reached, if possible.
There are several ways to implement this solution, as well as their additions. Some of them improved performance, while others only pointed out the weaknesses of Dijkstra’s solution, since it only works with positively weighted graphs — such where there are no negative weights for relationships.
For example, take the following positive graph and present it through the list, where we indicate the connection between the nodes:

We implement the algorithm using the priority queue to create a list of all "non-optimized" nodes:
You may notice that Dijkstra's solution is a simple search option in width. Let's go back to the example and try it out:
Everything. On it, apparently, articles from Ignatius Teo on structures have ended. I thank everyone who read, I didn’t expect that the first part will be placed by so many people into favorites, although we all know that favorites are rarely read and all posts remain there forever :)
Performance benchmarks for implementations of these scopipastil structures from here
Unlike the previous article, here the choice in favor of SPL implementations over ordinary arrays is obvious - using them gives more operations that can be performed in a second + less memory is used.
As usual, in lichku my mistakes are accepted in the text, translation, conflicting information, as well as impudent lies.
Comments welcome discussion and subsequent additions to the article.
At the end of the last article, trees were touched upon, so let's start with a heap, since there are common roots between the heap and the trees. Then we go to the graphs and implement the Dijkstra algorithm.
UPD : Added performance comparison
A heap is a special, tree-like structure that has one property — any parent node is always greater or equal to its descendants. Thus, if this condition is met, the root element of the heap will always be maximal. This option is called the maximum (full) heap or maxheap. The heap where the root element is minimal and each parent node is less than or equal to its descendants is the minimal heap or minheap.
')
Binary heap (maxheap) can be represented as follows:

It is binary because each parent has two children.
It should be noted that heaps, though implemented as binary trees, but they do not have such a thing as ordering and there is no specific order for traversing. A heap is a variant of a table structure, therefore the following basic operations are applicable to it:
- create - create an empty heap.
- isEmpty - determine if the heap is empty or not.
- insert - add an item to the heap.
- extract - extract and remove an element (root, vertex) from the heap.
Since the operations of receiving and deleting elements are combined in one extraction operation, we will consider it for the beginning.
The rule for removing an element from a heap is that only the root element can be deleted. Suppose we have removed the root element from the example above (100). After deletion, we will be left with two separate heaps and we need to somehow rebuild it all into one separate heap. It is easiest to do this by moving the last node to the root, but in this case such a heap will not be suitable for the main condition. Such a pile is called semiheap:

Now it is necessary to make a normal pile out of half a heap. One of the possible solutions to this problem is to lower the new root downwards, simultaneously comparing the root element with its descendants and changing its places with the maximum descendant. Thus, we will return the maximum element to the root, while lowering the minimum to the maximum.
We can implement maxheap as an array. A node in a binary tree cannot have more than two children, so for any number of nodes n a binary heap will have 2n + 1 nodes.
We implement a bunch as follows:
<?php class BinaryHeap { protected $heap; public function __construct() { $this->heap = array(); } public function isEmpty() { return empty($this->heap); } public function count() { // return count($this->heap) - 1; } public function extract() { if ($this->isEmpty()) { throw new RunTimeException(' !'); } // $root = array_shift($this->heap); if (!$this->isEmpty()) { // // $last = array_pop($this->heap); array_unshift($this->heap, $last); // $this->adjust(0); } return $root; } public function compare($item1, $item2) { if ($item1 === $item2) { return 0; } // minheap return ($item1 > $item2 ? 1 : -1); } protected function isLeaf($node) { // 2n + 1 "" return ((2 * $node) + 1) > $this->count(); } protected function adjust($root) { // if (!$this->isLeaf($root)) { $left = (2 * $root) + 1; // $right = (2 * $root) + 2; // $h = $this->heap; // if ( (isset($h[$left]) && $this->compare($h[$root], $h[$left]) < 0) || (isset($h[$right]) && $this->compare($h[$root], $h[$right]) < 0) ) { // if (isset($h[$left]) && isset($h[$right])) { $j = ($this->compare($h[$left], $h[$right]) >= 0) ? $left : $right; } else if (isset($h[$left])) { $j = $left; // } else { $j = $right; // } // list($this->heap[$root], $this->heap[$j]) = array($this->heap[$j], $this->heap[$root]); // // $j $this->adjust($j); } } } } Insertion is the opposite, the exact opposite of extraction: we insert an element down the heap and raise it until it is possible and the main condition is met. Since we know that a full binary tree contains an n / 2 + 1 node, we can bypass the heap using a simple binary search.
public function insert($item) { // $this->heap[] = $item; // $place = $this->count(); $parent = floor($place / 2); // while ( $place > 0 && $this->compare( $this->heap[$place], $this->heap[$parent]) >= 0 ) { // list($this->heap[$place], $this->heap[$parent]) = array($this->heap[$parent], $this->heap[$place]); $place = $parent; $parent = floor($place / 2); } } Let's see what we did and try to insert several values into the heap:
<?php $heap = new BinaryHeap(); $heap->insert(19); $heap->insert(36); $heap->insert(54); $heap->insert(100); $heap->insert(17); $heap->insert(3); $heap->insert(25); $heap->insert(1); $heap->insert(67); $heap->insert(2); $heap->insert(7); If we try to derive all this, we get the following:
Array ( [0] => 100 [1] => 67 [2] => 54 [3] => 36 [4] => 19 [5] => 7 [6] => 25 [7] => 1 [8] => 17 [9] => 2 [10] => 3 ) As you can see, the order is not observed, and in general this is somewhat different than what we expected. However, if we in turn take elements from the heap, then everything will be fine:
<?php while (!$heap->isEmpty()) { echo $heap->extract() . "n"; } 100 67 54 36 25 19 17 7 3 2 1 SplMaxHeap and SplMinHeap
Fortunately, we already have ready-made implementations of SplHeap, SplMaxHeap and SplMinHeap. All we need to do is just to inherit them and override the comparison method, like this:
<?php class MyHeap extends SplMaxHeap { public function compare($item1, $item2) { return (int) $item1 - $item2; } } This method will perform any comparison of two nodes, and in the case of SplMaxHeap, it returns a positive number if $ item1 is greater than $ item2, 0 if they are equal to each other, and negative if $ item2 is greater than $ item1. If we inherit SplMinHeap, then it will return a positive number if $ item1 is less than $ item2.
It is not recommended to put several identical elements in a heap, since their position will be difficult to determine
SplPriorityQueue - priority queue
A priority queue is a special abstract data type that behaves like a queue, but is implemented as a heap. Regarding the SplPriorityQueue this will be maxheap The priority queue has quite a few real-world applications, for example, a ticket system or help desk.
As in the case of SplHeap, you only need to inherit the SplPriorityQueue and override the comparison method:
<?php class PriQueue extends SplPriorityQueue { public function compare($p1, $p2) { if ($p1 === $p2) return 0; // , // return ($p1 < $p2) ? 1 : -1; } } The main difference in SplPriorityQueue is that when inserting, in addition to the element value, the priority of this element is also expected. The insert operation uses priority to sift through the heap based on the result that your comparator returns.
Let's check the work of the priority queue, set the numbers as numbers:
<?php $pq = new PriQueue(); $pq->insert('A', 4); $pq->insert('B', 3); $pq->insert('C', 5); $pq->insert('D', 8); $pq->insert('E', 2); $pq->insert('F', 7); $pq->insert('G', 1); $pq->insert('H', 6); $pq->insert('I', 0); while ($pq->valid()) { print_r($pq->current()); echo "n"; $pq->next(); } What ultimately will give us the following:
I G E B A C H F D In this case, our elements go in descending order of priority - from the highest to the lowest (lower value means higher priority). You can change the order in which items are returned by simply changing the comparison method so that it returns a positive number if $ p1 is greater than $ p2.
By default, only the value of the element is retrieved. If you want to get only the values of the priority, or the values and their priority, you need to set the appropriate flag to extract:
<?php // $pq->setExtractFlags(SplPriorityQueue::EXTR_PRIORITY); // ( // ) $pq->setExtractFlags(SplPriorityQueue::EXTR_BOTH); Counts
Behind the graphs there are quite a few real-world applications — network optimization, routing, or analysis of social networks. Google PageRank, recommendations from Amazon are some examples of their use. In this part of the article I will try to explain two tasks in which they are used - problems finding a short cut and the least number of stops.
A graph is a mathematical construct used to represent relationships between key-value pairs. A graph consists of a set of vertices (nodes) and an arbitrary number of connections between nodes connecting them to each other. These links can be directional (oriented) and non-directional. A directional link is a link between two nodes and the link A → B is not the same as B → A. The non-directional link has no direction, so the AB and BA links are identical. Based on these rules, we can say that trees are one of the undirected graphs, where each vertex is connected to one of the nodes by a simple link.
Counts can also have weight. A weighted graph, or a network, is a graph whose weight is indicated for each connection (the “price” of the transition from node A to node B). Such constructions are widely used to determine the most optimal path, or the most “cheap” path between two points. Laying the way in GoogleMap is carried out with the help of a weighted graph.
Minimum number of stops (jumps)
The general application of graph theory is used when searching for the minimum number of stops between two nodes. As for trees, here the graphs help in traversing the tree in one of two directions - in depth or in width. Since last time we considered the search in depth, now let's take a look at another method.
Imagine the following graph:
For simplicity, we agree that this graph is undirected. The task is to find the minimum number of stops between any two nodes. When searching in width, we start from the root (well, or from another node, which we denote as root) and go down the tree level by level. To implement this, we need a queue to organize a list of nodes that we have not yet walked around in order to return to it and process it at each level. The general algorithm is as follows:
- 1. Create a queue
- 2. Add the root element there and mark it as visited
- 3. Until the queue is empty:
- 3a. extract current node
- 3b. if the current node is the desired one, we stop
- 3c. otherwise, add each unvisited neighbor node to the queue and mark it as visited
But how do we know which nodes are adjacent or unvisited without resorting to traversing the graph? This brings us to the question of how graphs can be modeled.
Graph representation
Usually, graphs are represented in two ways - a table or a matrix, where neighboring nodes are described.
Here is how it looks for the first example:


In the matrix, at the intersection of nodes is put "1", if the nodes are neighbors.
The list is useful if most of the vertices do not have connections between themselves, the matrix provides a faster search. In the end, the type of representation of the graph depends on what operations with the graph will be performed. We will use the list.
<?php $graph = array( 'A' => array('B', 'F'), 'B' => array('A', 'D', 'E'), 'C' => array('F'), 'D' => array('B', 'E'), 'E' => array('B', 'D', 'F'), 'F' => array('A', 'E', 'C'), ); And write our search in width:
<?php class Graph { protected $graph; protected $visited = array(); public function __construct($graph) { $this->graph = $graph; } // () 2 public function breadthFirstSearch($origin, $destination) { // foreach ($this->graph as $vertex => $adj) { $this->visited[$vertex] = false; } // $q = new SplQueue(); // $q->enqueue($origin); $this->visited[$origin] = true; // $path = array(); $path[$origin] = new SplDoublyLinkedList(); $path[$origin]->setIteratorMode( SplDoublyLinkedList::IT_MODE_FIFO|SplDoublyLinkedList::IT_MODE_KEEP ); $path[$origin]->push($origin); $found = false; // while (!$q->isEmpty() && $q->bottom() != $destination) { $t = $q->dequeue(); if (!empty($this->graph[$t])) { // foreach ($this->graph[$t] as $vertex) { if (!$this->visited[$vertex]) { // , $q->enqueue($vertex); $this->visited[$vertex] = true; // $path[$vertex] = clone $path[$t]; $path[$vertex]->push($vertex); } } } } if (isset($path[$destination])) { echo " $origin $destination ", count($path[$destination]) - 1, " "; $sep = ''; foreach ($path[$destination] as $vertex) { echo $sep, $vertex; $sep = '->'; } echo "n"; } else { echo " $origin $destinationn"; } } } By running this example we get the following:
Look at the graph again
<?php $g = new Graph($graph); // D C $g->breadthFirstSearch('D', 'C'); // : // D C 3 // D->E->F->C // B F $g->breadthFirstSearch('B', 'F'); // : // B F 2 // B->A->F // A C $g->breadthFirstSearch('A', 'C'); // : // A C 2 // A->F->C // A G $g->breadthFirstSearch('A', 'G'); // : // A G If we used the stack instead of the queue, then the round would be in depth.
Search for the best path
Another common problem is finding the optimal path between any two nodes. Earlier, I already spoke about building a route in GoogleMaps as an example of solving this problem. Alternatively, this task can be applied to routing, traffic management, and so on.
One of the famous algorithms aimed at solving this problem was invented in 1959 by a 29-year-old scientist named Edsger Wibe Dijkstra . You can learn more about the algorithm in Wikipedia or look at it at the splitface . In general, Dijkstra’s solution comes down to checking each connection between all possible pairs of nodes, starting from the starting node, and maintaining an updated set of nodes with the shortest distance until the target node is reached, if possible.
There are several ways to implement this solution, as well as their additions. Some of them improved performance, while others only pointed out the weaknesses of Dijkstra’s solution, since it only works with positively weighted graphs — such where there are no negative weights for relationships.
For example, take the following positive graph and present it through the list, where we indicate the connection between the nodes:

<?php $graph = array( 'A' => array('B' => 3, 'D' => 3, 'F' => 6), 'B' => array('A' => 3, 'D' => 1, 'E' => 3), 'C' => array('E' => 2, 'F' => 3), 'D' => array('A' => 3, 'B' => 1, 'E' => 1, 'F' => 2), 'E' => array('B' => 3, 'C' => 2, 'D' => 1, 'F' => 5), 'F' => array('A' => 6, 'C' => 3, 'D' => 2, 'E' => 5), ); We implement the algorithm using the priority queue to create a list of all "non-optimized" nodes:
<?php class Dijkstra { protected $graph; public function __construct($graph) { $this->graph = $graph; } public function shortestPath($source, $target) { // $d = array(); // "" $pi = array(); // $Q = new SplPriorityQueue(); foreach ($this->graph as $v => $adj) { $d[$v] = INF; // $pi[$v] = null; // foreach ($adj as $w => $cost) { // $Q->insert($w, $cost); } } // - 0 $d[$source] = 0; while (!$Q->isEmpty()) { // $u = $Q->extract(); if (!empty($this->graph[$u])) { // foreach ($this->graph[$u] as $v => $cost) { // $alt = $d[$u] + $cost; // if ($alt < $d[$v]) { $d[$v] = $alt; // update minimum length to vertex $pi[$v] = $u; // } } } } // // $S = new SplStack(); // $u = $target; $dist = 0; // while (isset($pi[$u]) && $pi[$u]) { $S->push($u); $dist += $this->graph[$u][$pi[$u]]; // $u = $pi[$u]; } // , if ($S->isEmpty()) { echo " $source $targetn"; } else { // // (LIFO) $S->push($source); echo "$dist:"; $sep = ''; foreach ($S as $v) { echo $sep, $v; $sep = '->'; } echo "n"; } } } You may notice that Dijkstra's solution is a simple search option in width. Let's go back to the example and try it out:
<?php $g = new Dijkstra($graph); $g->shortestPath('D', 'C'); // 3:D->E->C $g->shortestPath('C', 'A'); // 6:C->E->D->A $g->shortestPath('B', 'F'); // 3:B->D->F $g->shortestPath('F', 'A'); // 5:F->D->A $g->shortestPath('A', 'G'); // A G Everything. On it, apparently, articles from Ignatius Teo on structures have ended. I thank everyone who read, I didn’t expect that the first part will be placed by so many people into favorites, although we all know that favorites are rarely read and all posts remain there forever :)
Performance benchmarks for implementations of these scopipastil structures from here
take a look







Unlike the previous article, here the choice in favor of SPL implementations over ordinary arrays is obvious - using them gives more operations that can be performed in a second + less memory is used.
As usual, in lichku my mistakes are accepted in the text, translation, conflicting information, as well as impudent lies.
Comments welcome discussion and subsequent additions to the article.
Source: https://habr.com/ru/post/190474/
All Articles