Collision with a wall at a speed of 100 km / h, an unpleasant surprise

Two identical cars, each of which moves at a speed of 100 km / h, collide head-on. Is this a collision with a concrete wall at a speed of 200 km / h?

An absolutely elastic cyclist at a speed of 100 km / h collides head-on with a heavy train, also moving at a speed of 100 km / h. Does the cyclist bounce at a speed of 300 km / h?

If you answered the questions " no, yes, " then you are right and I will not tell you anything new. And I invite the rest under the cat. There is no sophistry there.

Clash of two cars

In reality, a head-on collision of identical cars at a speed of 100 km / h is equivalent to a collision with a heavy wall at a speed of 100 km / h. Let's try to figure it out.
')
Consider the center of mass of these two machines, it is strictly in the middle between them. During the collision, this center is not shifted. Moreover, it does not matter if the cars are absolutely resilient, absolutely inelastic or real. So at this point we can put up a virtual wall. Note also that each of the two machines will absorb half of the total energy of the system. Exactly the same energy ( mV 2/2 ) absorbs the car, flying into the wall at the same speed.

Thus, comparing this collision with a collision of 200 km / h is illegal.

Clash of a cyclist with a train

We show that the absolutely elastic cyclist will bounce off the train at a speed of 300 km / h.

Absolute elasticity will allow the cyclist not to turn into a cake, having lost all his energy and speed, and also to travel further on the windshield of the train.

Let the speed of the cyclist v , and the speed of the train W. The speeds are scalar (Figure 1).

1. For a start, let's go into the train reference system. According to the speed addition theorem, it will turn into a fixed object, but the bicycle speed will increase and become equal to v + W (Figure 2)
2. Since the impact is absolutely elastic, the cyclist bounces off at the same speed v + W (Figure 3)
3. Let us go back to the reference frame of the stationary observer. All objects will start moving left on W faster. The train will go again, and the speed of the cyclist will increase to v + 2W (Figure 4)
4. And since in our example v = W = 100 km / h, then the speed of the cyclist will be equal to 300 km / h.

Similar reasoning, taking into account the laws of conservation of pulses and energy, a formula is derived for velocities in the case of elastic collision.


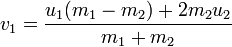
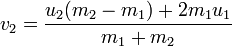
Here u _i are the speeds before the collision, v _i is the speeds after, and m _i are the masses. Speed ​​vector. By pushing m ₂ to infinity, we get the same result (do not forget that we have u ₁ and u _{2 in} different directions).

Conclusion

I hope the task is not too trivial for Habr's visitors, and my reasoning turned out to be clear to you. Otherwise, I risk being mined. If you do not agree with any of the points, or it is not sufficiently clear, please indicate the item number in the comment.

Have a nice Friday.