Representation of numbers by the sum of two squares and elliptic curves
Let p be an odd prime number. It is widely known that p is representable as the sum of two squares of integers p = a 2 + b 2 if and only if p when divided by 4 gives the remainder 1: 5 = 1 2 + 2 2 , 13 = 3 2 + 2 2 , 17 = 1 2 + 4 2 , ...; 3, 7, 11, ... not representable. Far less well known is that a and b can be written with a beautiful formula that is directly related to a single elliptic curve. About this result in 1907 for the authorship of a German by the name of Jacobsthal and related things, we will talk today.
It is quite easy to understand why 3, 7, 11 and other numbers that give a remainder of 3 when divided by 4 are not representable as a 2 + b 2 : a square of an even number is always divisible by 4, a square of an odd number always gives a remainder of 1 when divided by 4 , the sum of two squares when divided by 4 can give residues of 0, 1 or 2, but not 3. The primacy of primes like 4k + 1 is not obvious (especially if you notice that simplicity is significant: the number 21 does have the necessary remainder, but the sum of two squares are not represented).
There are infinitely many natural numbers. It can be useful to combine them into classes for some signs. In particular, combining by the remainder of dividing by some number n leads to deductions modulo n : the deduction x is the class of all numbers that, when divided by n, give the same remainder as x . That is equivalent, the residue x̅ consists of all numbers of the form x + n ∙ k , where k is integer. Within this post, all deductions will be modulo p (the same odd prime number from the introduction). Naturally, there are as many different residues as there can be residues from division by p , that is, exactly p . Compared to the infinity of natural numbers, the transition to deductions greatly reduces the number of options.
Class operations do not always make sense. For example, an attempt to add a class of prime numbers with a class of composite numbers is not very meaningful: we can only add numbers, while the sum of a prime number and a composite number does not show the properties common to the class. Although members of the tautology club can say that the addition of the class of prime numbers and the class of composite numbers gives a class of numbers that are decomposed into the sum of a prime number and a composite number.
')
For deductions, however, addition, subtraction and multiplication, “inherited” from natural numbers, give other deductions. For example, 2̅ + 3̅ = 5̅: take any number with a remainder of 2, any number with a remainder of 3, and their sum will necessarily give a remainder of 5. Generally speaking, the product of two nonzero residues over an arbitrary module may suddenly turn out to be zero, 2̅ 3̅ = 0̅ by module 6, which is unpleasant. But in the case of a simple module, obviously, this does not happen, as they say, there are no zero divisors . In addition, you can solve the equation a̅ ∙ x̅ = b̅ (division operation) for any two residues, except for the case a̅ = 0̅ , and the result will be uniquely determined. Uniqueness follows from the fact that the product of nonzero residues is nonzero. Since a̅ ≠ 0̅ , the greatest common divisor of a and p is 1 (simplicity p is also needed here), the advanced Euclidean algorithm will find x and y such that a ∙ x + p ∙ y = 1 , which implies a̅ ∙ x̅ = 1̅ , so, a̅ ∙ (b̅ ∙ x̅) = b̅ .
An important consequence of the absence of zero divisors: a non-zero polynomial in one variable of degree n cannot have more than n roots. (This is well known for ordinary integers, but when using operations on residues it requires additional justification: the equation 3̅ ∙ x̅ = 0̅ modulo 6 has three solutions 0̅, 2̅, 4̅.) Indeed, the usual “by column” division shows that any the f (x) polynomial can be represented as f (x) = (x-) g (x) + (some constant), where the g (x) polynomial has a degree less than one; if c is the root of f (x) , then the constant is zero (we substitute x = c ); if c ' is another f (x) , then it will be g (x) (the absence of zero divisors is important here), so the process can be continued. If n roots have already been gathered, then the remaining g (x) will be constant, and non-zero (otherwise f (x) = 0 ) and has no more roots.
Deductions on a simple module can be added, subtracted, multiplied. Non-zero deductions can be divided. All these operations have the usual properties of the type a̅ ∙ b̅ = b̅ ∙ a̅ . Smart books say that deductions by a simple module form a field (and deductions by a composite module, where it is impossible to divide, and everything else is the same, a commutative ring ). And you do not need to be a smart book to call this field finite . The residue field is not the only finite field, but we will not need other finite fields.
An elliptic curve modulo p (that odd prime number) can be viewed as a set of solutions to the equation y 2 = x 3 + a 2 x 2 + a 4 x + a 6 , where x , y and all a are residues (each solution is called one point ), plus one special point O , not having a pair of x, y . The right side of the equation should not be divisible by a square, otherwise it will not be an elliptic curve: in an equation of the type y 2 = (x-1̅) 2 (x + 2̅), you can replace the variable y with z = y / (x-1̅) and get the dependence second degree, not third.
If p ≠ 3 , then instead of the variable x you can take x + a 2 / 3̅ , getting rid of the term with x 2 .
It is clear that since x, y belong to a finite set, then the number of points on an elliptic curve is also finite. How many of them? This is a difficult question in general. We restrict ourselves to curves of the form y 2 = x 3 -k ∙ x . For such curves, the full proof can be put in one Habr's post (albeit rather long).
Let us first ask a simpler question. How many solutions does the equation y 2 = c , where y, c are residues? Example for p = 7 :
If c = 0̅ , then the solution is one, y = 0̅ . The remaining values of y are divided into two halves, from 1̅ before the deduction corresponding to (p-1) / 2 , and from the deduction corresponding to (p + 1) / 2 , to -1 . Once y 2 = (- y) 2 , the second half of the row of values of y 2 is mirror-symmetric to the first half. On the other hand, in each half there are no repetitions, since otherwise the equation would have at least 4 solutions, which is impossible for a polynomial of degree 2. Hence, there are (p-1) / 2 c residues for which there are exactly 2 solutions, and the same c residues for which there are no solutions at all.
Nonzero c residues for which there is a solution are called quadratic residues . The residues c , for which there is no solution, are called quadratic non-residues . It is worth noting that a quadratic non-derivation is a deduction, it’s just not lucky to be quadratic. Legendre Symbol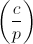
shows the ratio of c to squares: 1, if relevant (that is, c is a quadratic residue), -1, if not applicable (that is, c is a quadratic non-residue), 0, if c = 0 . The number of solutions to the equation y 2 = c is equal to 
.
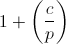Let us return to the elliptic curves. The number of options y for a fixed x we know, the total number of points on the curve y 2 = x 3 -k ∙ x can be written by summing over all x and not forgetting the special point: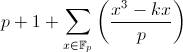
. The symbol F p , which has never appeared before, is usually denoted as a field of residues modulo p .
Now we are ready to present the promised formulas for the components of the decomposition of p in the sum of two squares. Theorem . Let g be any quadratic non-counting. If p when divided by 4 gives the remainder 1, then
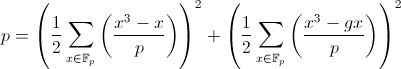
and the number in the first bracket is an odd integer, the number in the second bracket is an even integer. If p, when divided by 4, gives the remainder of 3, then both sums in brackets are zero (and therefore, the number of points on elliptic curves is p + 1 ).
Since the post is already long, the evidence is removed under the spoiler. You can safely skip it without affecting perception.
It is impractical to calculate a and b , counting p times the Legendre symbols. Much faster with this Cornacchia algorithm . The practical benefit is to use the formula for a, b in the opposite direction: it is possible to prove that the decomposition p = a 2 + b 2 is unique up to a permutation of a and b and a change of signs, so finding a and b leads to knowing the number of points on the curves y 2 = x 3 -t ∙ x for any non-zero t , it will be p + 1 ± 2a and p + 1 ± 2b .
Knowing the number of points on a curve is important for cryptography on this curve. On an elliptic curve, you can enter the operation of adding points (about which, probably, everyone who knows at least something about cryptography) with a special point O in the role of zero. On the basis of the addition operation, one can determine the multiplication by a natural number: 2P = P + P , 3P = P + P + P, and so on. So, we can prove that if n is the order of a curve, then nP = O for any point P. Knowing n, c, d , one can solve equations of the form x ∙ (cP) = dP is completely analogous to the division of residues: the advanced Euclidean algorithm finds x, y such that c ∙ x + n ∙ y = 1 , whence x ∙ (cP) + y ∙ (nP) = P , that is, x ∙ (cP) = P. Moreover, if c, d are unknown, and cP and dP are given by coordinates, then effective division methods are generally unknown.
It is quite difficult to calculate the number of points on a given curve (a polynomial algorithm exists, but in practice it is rather slow). To build a curve with some properties on the number of points, you can try to take random coefficients and calculate the number of points in the cycle until you get what you need, but you have to wait. Fortunately, there is another way.
If we are satisfied with a prime number of the form 4k + 1 and a special curve of the form y 2 = x 3 -t ∙ x (in some sense this is the same curve for any nonzero t ) with the number of points p + 1 ± 2a or p + 1 ± 2b , you can take it. What about the other curves?
A little later, in 1911, another author, von Schrutka, obtained a similar result for curves of the form y 2 = x 3 -t , simple ones of the form 6k + 1 , and representations p = a 2 + 3b 2 . So, the Cornacchia algorithm allows to find the number of points on the curve y 2 = x 3 -t .
Later, as the theory of elliptic curves developed, it turned out that if there is some representation 4p = a ' 2 + d ∙ b' 2 , where d is natural, when divided by 4, it gives the remainder 0 or 3, mutually simple with p and not too large, it is possible to effectively (even if p is very large) to construct a curve that will have exactly p + 1 ± a ' points. The two smallest values d = 3 and d = 4 correspond to the curves y 2 = x 3 -t and y 2 = x 3 -t x . Example for d = 163 :
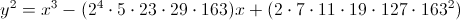
For odd p ≠ 163, this equation defines an elliptic curve. If 4p can be represented as a ' 2 + 163b' 2 with integers a ', b' , then the number of points on an elliptic curve is p + 1 ± a ' . If not, then p + 1 . Unfortunately, the proof uses a "heavy" theory, so there will not even be hints here.
Usually, however, radicals will be obtained. For example, for d = 15 :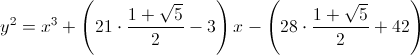
. If 4p decomposes into a sum a ' 2 + d ∙ b' 2 and p is mutually simple with d , then all radicals are necessarily extracted (for example, for d = 15 there is necessarily a residue c , for which c 2 = 5̅ ) and we get an elliptic curve with the required number of points.
It is quite easy to understand why 3, 7, 11 and other numbers that give a remainder of 3 when divided by 4 are not representable as a 2 + b 2 : a square of an even number is always divisible by 4, a square of an odd number always gives a remainder of 1 when divided by 4 , the sum of two squares when divided by 4 can give residues of 0, 1 or 2, but not 3. The primacy of primes like 4k + 1 is not obvious (especially if you notice that simplicity is significant: the number 21 does have the necessary remainder, but the sum of two squares are not represented).
Deductions
There are infinitely many natural numbers. It can be useful to combine them into classes for some signs. In particular, combining by the remainder of dividing by some number n leads to deductions modulo n : the deduction x is the class of all numbers that, when divided by n, give the same remainder as x . That is equivalent, the residue x̅ consists of all numbers of the form x + n ∙ k , where k is integer. Within this post, all deductions will be modulo p (the same odd prime number from the introduction). Naturally, there are as many different residues as there can be residues from division by p , that is, exactly p . Compared to the infinity of natural numbers, the transition to deductions greatly reduces the number of options.
Class operations do not always make sense. For example, an attempt to add a class of prime numbers with a class of composite numbers is not very meaningful: we can only add numbers, while the sum of a prime number and a composite number does not show the properties common to the class. Although members of the tautology club can say that the addition of the class of prime numbers and the class of composite numbers gives a class of numbers that are decomposed into the sum of a prime number and a composite number.
')
For deductions, however, addition, subtraction and multiplication, “inherited” from natural numbers, give other deductions. For example, 2̅ + 3̅ = 5̅: take any number with a remainder of 2, any number with a remainder of 3, and their sum will necessarily give a remainder of 5. Generally speaking, the product of two nonzero residues over an arbitrary module may suddenly turn out to be zero, 2̅ 3̅ = 0̅ by module 6, which is unpleasant. But in the case of a simple module, obviously, this does not happen, as they say, there are no zero divisors . In addition, you can solve the equation a̅ ∙ x̅ = b̅ (division operation) for any two residues, except for the case a̅ = 0̅ , and the result will be uniquely determined. Uniqueness follows from the fact that the product of nonzero residues is nonzero. Since a̅ ≠ 0̅ , the greatest common divisor of a and p is 1 (simplicity p is also needed here), the advanced Euclidean algorithm will find x and y such that a ∙ x + p ∙ y = 1 , which implies a̅ ∙ x̅ = 1̅ , so, a̅ ∙ (b̅ ∙ x̅) = b̅ .
An important consequence of the absence of zero divisors: a non-zero polynomial in one variable of degree n cannot have more than n roots. (This is well known for ordinary integers, but when using operations on residues it requires additional justification: the equation 3̅ ∙ x̅ = 0̅ modulo 6 has three solutions 0̅, 2̅, 4̅.) Indeed, the usual “by column” division shows that any the f (x) polynomial can be represented as f (x) = (x-) g (x) + (some constant), where the g (x) polynomial has a degree less than one; if c is the root of f (x) , then the constant is zero (we substitute x = c ); if c ' is another f (x) , then it will be g (x) (the absence of zero divisors is important here), so the process can be continued. If n roots have already been gathered, then the remaining g (x) will be constant, and non-zero (otherwise f (x) = 0 ) and has no more roots.
Deductions on a simple module can be added, subtracted, multiplied. Non-zero deductions can be divided. All these operations have the usual properties of the type a̅ ∙ b̅ = b̅ ∙ a̅ . Smart books say that deductions by a simple module form a field (and deductions by a composite module, where it is impossible to divide, and everything else is the same, a commutative ring ). And you do not need to be a smart book to call this field finite . The residue field is not the only finite field, but we will not need other finite fields.
A little bit about elliptic curves
An elliptic curve modulo p (that odd prime number) can be viewed as a set of solutions to the equation y 2 = x 3 + a 2 x 2 + a 4 x + a 6 , where x , y and all a are residues (each solution is called one point ), plus one special point O , not having a pair of x, y . The right side of the equation should not be divisible by a square, otherwise it will not be an elliptic curve: in an equation of the type y 2 = (x-1̅) 2 (x + 2̅), you can replace the variable y with z = y / (x-1̅) and get the dependence second degree, not third.
If p ≠ 3 , then instead of the variable x you can take x + a 2 / 3̅ , getting rid of the term with x 2 .
It is clear that since x, y belong to a finite set, then the number of points on an elliptic curve is also finite. How many of them? This is a difficult question in general. We restrict ourselves to curves of the form y 2 = x 3 -k ∙ x . For such curves, the full proof can be put in one Habr's post (albeit rather long).
Quadratic deductions and non-deductions
Let us first ask a simpler question. How many solutions does the equation y 2 = c , where y, c are residues? Example for p = 7 :
| y | 0̅ | one | 2̅ | 3̅ | four | five | 6̅ |
| y 2 | 0̅ | one | four | 2̅ | 2̅ | four | one |
Nonzero c residues for which there is a solution are called quadratic residues . The residues c , for which there is no solution, are called quadratic non-residues . It is worth noting that a quadratic non-derivation is a deduction, it’s just not lucky to be quadratic. Legendre Symbol
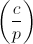shows the ratio of c to squares: 1, if relevant (that is, c is a quadratic residue), -1, if not applicable (that is, c is a quadratic non-residue), 0, if c = 0 . The number of solutions to the equation y 2 = c is equal to 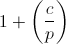.Let us return to the elliptic curves. The number of options y for a fixed x we know, the total number of points on the curve y 2 = x 3 -k ∙ x can be written by summing over all x and not forgetting the special point:
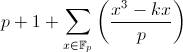. The symbol F p , which has never appeared before, is usually denoted as a field of residues modulo p .Now we are ready to present the promised formulas for the components of the decomposition of p in the sum of two squares. Theorem . Let g be any quadratic non-counting. If p when divided by 4 gives the remainder 1, then
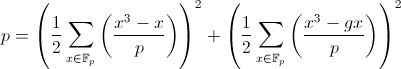
and the number in the first bracket is an odd integer, the number in the second bracket is an even integer. If p, when divided by 4, gives the remainder of 3, then both sums in brackets are zero (and therefore, the number of points on elliptic curves is p + 1 ).
Evidence
Since the post is already long, the evidence is removed under the spoiler. You can safely skip it without affecting perception.
Part 1. The case of p = 4k + 3 and parity / oddness problems.
If we take a nonzero residue c and multiply it by all residues from 1̅ to p̅-1̅ , all products will be non-zero and pairwise different (if c ∙ x = c ∙ y , then c ∙ (xy) = 0̅ , which with non-zero c can be only if x = y ), which means that it will simply be some kind of permutation of all residues from 1̅ to p̅-1̅ . Therefore, 1̅ ∙ 2̅ ∙ ... ∙ (p̅-1̅) = (c ∙ 1̅) (c ∙ 2̅) ∙ ... ∙ (c ∙ (p̅-1̅)) = c p-1 1̅ ∙ 2̅ ∙ ... ∙ (p̅-1̅) and c p-1 = 1̅ for any nonzero residue c . (This was the proof of Fermat's small theorem .)
Therefore, the polynomial x p-1 -1 = (x (p-1) / 2 -1) (x (p-1) / 2 +1) has p-1 roots. This means that each bracket has (p-1) / 2 roots (the maximum possible number for the degree of brackets). Each quadratic residue is the root of the first bracket (if x = c 2 , then x (p-1) / 2 = c p-1 = 1̅ ), their (p-1) / 2 , which means that all square non-counting remains the second bracket. So, the Legendre symbol from c belongs to the same deduction as c (p-1) / 2 . (This was proof of Euler's criterion ).
As a result, we get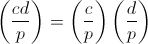
.
Is -1̅ a quadratic residue? Depends on the sign (-1) (p-1) / 2 . If p when divided by 4 gives the remainder 1, then (p-1) / 2 is even, (-1) (p-1) / 2 = 1 , -1 ̅ is a quadratic residue. If p when divided by 4 gives the remainder of 3, then the opposite is true and -1̅ is a quadratic non-count.
The simple part of the theorem: p gives the remainder of 3 when divided by 4. Then in each bracket the terms with x and -x differ from each other by multiplying by the Legendre symbol from –1̅, that is, they are opposite in sign and total to 0. Since all the terms, except x = 0̅ , they are divided into pairs with a zero sum, and the term with x = 0 , zero, the whole sum is 0.
If p gives the remainder 1 when divided by 4, then the terms with x and -x are equal and their sum is even. This means that the whole sum is also even and the numbers in brackets are really integers. Parity / oddness after dividing in half is not much more complicated: in the first bracket of the theorem there are three zero terms, the other terms are divided into (p-3) / 2 pairs with a sum of ± 2 in each pair; for any sign when dividing by 4, the remainder is 2, the whole amount when dividing by 4 gives the remainder the same as p-3 , that is 2. After dividing in half, we get an odd number. In the second bracket of the theorem, there is only one zero summand and (p-1) / 2 pairs with ± 2, the total remainder from dividing by 4 is 0, after dividing in half an even number remains.
Therefore, the polynomial x p-1 -1 = (x (p-1) / 2 -1) (x (p-1) / 2 +1) has p-1 roots. This means that each bracket has (p-1) / 2 roots (the maximum possible number for the degree of brackets). Each quadratic residue is the root of the first bracket (if x = c 2 , then x (p-1) / 2 = c p-1 = 1̅ ), their (p-1) / 2 , which means that all square non-counting remains the second bracket. So, the Legendre symbol from c belongs to the same deduction as c (p-1) / 2 . (This was proof of Euler's criterion ).
As a result, we get
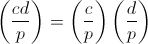.Is -1̅ a quadratic residue? Depends on the sign (-1) (p-1) / 2 . If p when divided by 4 gives the remainder 1, then (p-1) / 2 is even, (-1) (p-1) / 2 = 1 , -1 ̅ is a quadratic residue. If p when divided by 4 gives the remainder of 3, then the opposite is true and -1̅ is a quadratic non-count.
The simple part of the theorem: p gives the remainder of 3 when divided by 4. Then in each bracket the terms with x and -x differ from each other by multiplying by the Legendre symbol from –1̅, that is, they are opposite in sign and total to 0. Since all the terms, except x = 0̅ , they are divided into pairs with a zero sum, and the term with x = 0 , zero, the whole sum is 0.
If p gives the remainder 1 when divided by 4, then the terms with x and -x are equal and their sum is even. This means that the whole sum is also even and the numbers in brackets are really integers. Parity / oddness after dividing in half is not much more complicated: in the first bracket of the theorem there are three zero terms, the other terms are divided into (p-3) / 2 pairs with a sum of ± 2 in each pair; for any sign when dividing by 4, the remainder is 2, the whole amount when dividing by 4 gives the remainder the same as p-3 , that is 2. After dividing in half, we get an odd number. In the second bracket of the theorem, there is only one zero summand and (p-1) / 2 pairs with ± 2, the total remainder from dividing by 4 is 0, after dividing in half an even number remains.
Part 2. The case of p = 4k + 1.
Let p, when divided by 4, give the remainder 1. Denote the first bracket of the theorem by a , the second by b . We already know that a and b are integers.
For the proof, we calculate the following strange value N in two ways: the number of five residues ( x 1 , y 1 , x 2 , y 2 , t ) such that two equations are fulfilled at once: y 1 2 = x 1 3 -t ∙ x 1 and y 2 2 = x 2 3 -t ∙ x 2 .
In the first method, first fix t and calculate the number of fours of x, y , then add the results for all t . It is clear that for fixed t the pair ( x 1 , y 1 ) can be any non-special point of the curve y 2 = x 3 -t ∙ x , the second couple ( x 1 , y 1 ) - just as any non-special point of the same curve, and the total number of such pairs is equal to the square of the number of non-special points. (Actually, therefore, we consider a strange value, it allows you to get to a 2 and b 2. ) If t = 0 , then the equation y 2 = x 3 , as already mentioned, does not define an elliptic curve and has as many solutions as the equation z 2 = x (where y = z ∙ x ), that is, exactly p . For t = 1, we get p + 2a solutions, and for t = g - p + 2b solutions. What about the other t values?
If y 2 = x 3 -t ∙ x and c is some non-zero residue, then c 6 y 2 = c 6 x 3 -c 6 t ∙ x , which is equivalent to (c 3 y) 2 = (c 2 x) 3 -c 4 t ∙ (c 2 x) . In other words, if (x, y) is a solution of an equation with t , then (c 2 x, c 3 y) is a solution of an equation with c 4 t , so the number of solutions with t and c 4 t coincides. How many different non-zero c 4 cuts? On the one hand, at least (p-1) / 4 : (p-1) of c values can “stick together” into groups of no more than 4. On the other hand, if (p-1) / 4 is an integer, then all such residues are the roots of the polynomial x (p-1) / 4 -1 , so there cannot be more than (p-1) / 4 . This means that they are exactly (p-1) / 4 .
So, the (p-1) / 4 curves have p + 2a nonspecial points, and the (p-1) / 4 curves have p + 2b nonspecial points. This is already half of what is needed.
If y 2 = x 3 -t ∙ x , then g 3 y 2 = (g ∙ x) 3 - (g 2 t) (g ∙ x) . For a fixed x, the number of solutions of the equation g 3 y 2 = ... is 2 - the number of solutions of the equation y 2 = .... This means that the number of non-special points on a curve with t = g 2 (and therefore, on (p-1) / 4 similar curves) is 2p- (p + 2a) = p-2a . Similarly, the number of non- special points on a curve with t = g 3 is 2p- (p + 2b) = p-2b .
So, the first method of calculation gives
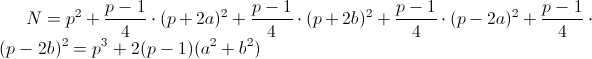
In the second method of calculating N, first fix x 1 and x 2 and count the number of triples t and y , then add the results for all pairs x . For x 1 = x 2 = 0̅, there are exactly p options: both y must be zeros, t can be any. When x 1 = 0̅ and non-zero x 2 should be y 1 = 0 , y 2 can be anything, t is calculated uniquely, it turns out again p options. The situation with zero x 2 and non-zero x 1 is symmetric. Finally, let both x be nonzero. Then t = x 1 2 - (y 1 2 / x 1 ) and you need to count the number of pairs y with the condition (x 2 / x 1 ) y 1 2 = y 2 2 + x 2 (x 1 2 -x 2 2 ) .
If x 1 = x 2 , then the equation turns into a condition of coincidence of squares y , and different pairs of y get 1 + 2 (p-1) : zero and two options y 2 for each non-zero y 1 . If x 1 = -x 2 , the situation is similar, since p gives the remainder 1 when divided by 4 and -1 ̅ is a quadratic residue.
If x 2 / x 1 is a quadratic residue not equal to ± 1̅, then there exists some nonzero c such that c 2 = x 2 / x 1 . Then (c 2 y 1 2 -y 2 2 ) = (c ∙ y 1 -y 2 ) (c ∙ y 1 + y 2 ) = x 2 (x 1 2 -x 2 2 ) , the expression c ∙ y 1 - y 2 can be any nonzero residue, it is uniquely determined by c ∙ y 1 + y 2 and, therefore, y 1 and y 2 . Total p-1 options.
If x 2 / x 1 is a quadratic non-counting, then, similarly to elliptic curves, the number of solutions is 2p minus the number of solutions in the case of a quadratic residue, that is, 2p- (p-1) = p + 1 .
Summing up. There is one option with x 1 = x 2 = 0 , giving p solutions. There are 2 (p-1) options, where one of x is zero and the other is non-zero, each of the options gives p solutions. There are 2 (p-1) variants with x 2 = ± x 1 , each of which gives 2p-1 solutions. There are (p-1) ((p-1) / 2-2) options, where x 1 is an arbitrary non-zero residue, and x 2 / x 1 is a quadratic residue that differs from ± 1̅, each of these options gives p-1 making. Finally, there are (p-1) 2/2 options, where x 1 is an arbitrary non-zero residue, and x 2 / x 1 is a non-residual quadratic, in each of these options, p + 1 solutions. Total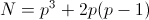
.
Comparison of two expressions for N completes the proof.
For the proof, we calculate the following strange value N in two ways: the number of five residues ( x 1 , y 1 , x 2 , y 2 , t ) such that two equations are fulfilled at once: y 1 2 = x 1 3 -t ∙ x 1 and y 2 2 = x 2 3 -t ∙ x 2 .
In the first method, first fix t and calculate the number of fours of x, y , then add the results for all t . It is clear that for fixed t the pair ( x 1 , y 1 ) can be any non-special point of the curve y 2 = x 3 -t ∙ x , the second couple ( x 1 , y 1 ) - just as any non-special point of the same curve, and the total number of such pairs is equal to the square of the number of non-special points. (Actually, therefore, we consider a strange value, it allows you to get to a 2 and b 2. ) If t = 0 , then the equation y 2 = x 3 , as already mentioned, does not define an elliptic curve and has as many solutions as the equation z 2 = x (where y = z ∙ x ), that is, exactly p . For t = 1, we get p + 2a solutions, and for t = g - p + 2b solutions. What about the other t values?
If y 2 = x 3 -t ∙ x and c is some non-zero residue, then c 6 y 2 = c 6 x 3 -c 6 t ∙ x , which is equivalent to (c 3 y) 2 = (c 2 x) 3 -c 4 t ∙ (c 2 x) . In other words, if (x, y) is a solution of an equation with t , then (c 2 x, c 3 y) is a solution of an equation with c 4 t , so the number of solutions with t and c 4 t coincides. How many different non-zero c 4 cuts? On the one hand, at least (p-1) / 4 : (p-1) of c values can “stick together” into groups of no more than 4. On the other hand, if (p-1) / 4 is an integer, then all such residues are the roots of the polynomial x (p-1) / 4 -1 , so there cannot be more than (p-1) / 4 . This means that they are exactly (p-1) / 4 .
So, the (p-1) / 4 curves have p + 2a nonspecial points, and the (p-1) / 4 curves have p + 2b nonspecial points. This is already half of what is needed.
If y 2 = x 3 -t ∙ x , then g 3 y 2 = (g ∙ x) 3 - (g 2 t) (g ∙ x) . For a fixed x, the number of solutions of the equation g 3 y 2 = ... is 2 - the number of solutions of the equation y 2 = .... This means that the number of non-special points on a curve with t = g 2 (and therefore, on (p-1) / 4 similar curves) is 2p- (p + 2a) = p-2a . Similarly, the number of non- special points on a curve with t = g 3 is 2p- (p + 2b) = p-2b .
So, the first method of calculation gives
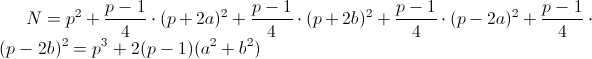
In the second method of calculating N, first fix x 1 and x 2 and count the number of triples t and y , then add the results for all pairs x . For x 1 = x 2 = 0̅, there are exactly p options: both y must be zeros, t can be any. When x 1 = 0̅ and non-zero x 2 should be y 1 = 0 , y 2 can be anything, t is calculated uniquely, it turns out again p options. The situation with zero x 2 and non-zero x 1 is symmetric. Finally, let both x be nonzero. Then t = x 1 2 - (y 1 2 / x 1 ) and you need to count the number of pairs y with the condition (x 2 / x 1 ) y 1 2 = y 2 2 + x 2 (x 1 2 -x 2 2 ) .
If x 1 = x 2 , then the equation turns into a condition of coincidence of squares y , and different pairs of y get 1 + 2 (p-1) : zero and two options y 2 for each non-zero y 1 . If x 1 = -x 2 , the situation is similar, since p gives the remainder 1 when divided by 4 and -1 ̅ is a quadratic residue.
If x 2 / x 1 is a quadratic residue not equal to ± 1̅, then there exists some nonzero c such that c 2 = x 2 / x 1 . Then (c 2 y 1 2 -y 2 2 ) = (c ∙ y 1 -y 2 ) (c ∙ y 1 + y 2 ) = x 2 (x 1 2 -x 2 2 ) , the expression c ∙ y 1 - y 2 can be any nonzero residue, it is uniquely determined by c ∙ y 1 + y 2 and, therefore, y 1 and y 2 . Total p-1 options.
If x 2 / x 1 is a quadratic non-counting, then, similarly to elliptic curves, the number of solutions is 2p minus the number of solutions in the case of a quadratic residue, that is, 2p- (p-1) = p + 1 .
Summing up. There is one option with x 1 = x 2 = 0 , giving p solutions. There are 2 (p-1) options, where one of x is zero and the other is non-zero, each of the options gives p solutions. There are 2 (p-1) variants with x 2 = ± x 1 , each of which gives 2p-1 solutions. There are (p-1) ((p-1) / 2-2) options, where x 1 is an arbitrary non-zero residue, and x 2 / x 1 is a quadratic residue that differs from ± 1̅, each of these options gives p-1 making. Finally, there are (p-1) 2/2 options, where x 1 is an arbitrary non-zero residue, and x 2 / x 1 is a non-residual quadratic, in each of these options, p + 1 solutions. Total
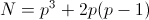.Comparison of two expressions for N completes the proof.
And here is cryptography?
It is impractical to calculate a and b , counting p times the Legendre symbols. Much faster with this Cornacchia algorithm . The practical benefit is to use the formula for a, b in the opposite direction: it is possible to prove that the decomposition p = a 2 + b 2 is unique up to a permutation of a and b and a change of signs, so finding a and b leads to knowing the number of points on the curves y 2 = x 3 -t ∙ x for any non-zero t , it will be p + 1 ± 2a and p + 1 ± 2b .
Knowing the number of points on a curve is important for cryptography on this curve. On an elliptic curve, you can enter the operation of adding points (about which, probably, everyone who knows at least something about cryptography) with a special point O in the role of zero. On the basis of the addition operation, one can determine the multiplication by a natural number: 2P = P + P , 3P = P + P + P, and so on. So, we can prove that if n is the order of a curve, then nP = O for any point P. Knowing n, c, d , one can solve equations of the form x ∙ (cP) = dP is completely analogous to the division of residues: the advanced Euclidean algorithm finds x, y such that c ∙ x + n ∙ y = 1 , whence x ∙ (cP) + y ∙ (nP) = P , that is, x ∙ (cP) = P. Moreover, if c, d are unknown, and cP and dP are given by coordinates, then effective division methods are generally unknown.
It is quite difficult to calculate the number of points on a given curve (a polynomial algorithm exists, but in practice it is rather slow). To build a curve with some properties on the number of points, you can try to take random coefficients and calculate the number of points in the cycle until you get what you need, but you have to wait. Fortunately, there is another way.
If we are satisfied with a prime number of the form 4k + 1 and a special curve of the form y 2 = x 3 -t ∙ x (in some sense this is the same curve for any nonzero t ) with the number of points p + 1 ± 2a or p + 1 ± 2b , you can take it. What about the other curves?
A little later, in 1911, another author, von Schrutka, obtained a similar result for curves of the form y 2 = x 3 -t , simple ones of the form 6k + 1 , and representations p = a 2 + 3b 2 . So, the Cornacchia algorithm allows to find the number of points on the curve y 2 = x 3 -t .
A couple of words about the evidence
The proof as a whole is similar to the above, only there are three numbers a, b 1 , b 2 for t = 1, g 2 , g 4 , where g is not a cube, their sum is zero, and the sum of squares is calculated. After simple transformations get what you need.
Later, as the theory of elliptic curves developed, it turned out that if there is some representation 4p = a ' 2 + d ∙ b' 2 , where d is natural, when divided by 4, it gives the remainder 0 or 3, mutually simple with p and not too large, it is possible to effectively (even if p is very large) to construct a curve that will have exactly p + 1 ± a ' points. The two smallest values d = 3 and d = 4 correspond to the curves y 2 = x 3 -t and y 2 = x 3 -t x . Example for d = 163 :
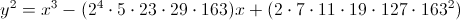
For odd p ≠ 163, this equation defines an elliptic curve. If 4p can be represented as a ' 2 + 163b' 2 with integers a ', b' , then the number of points on an elliptic curve is p + 1 ± a ' . If not, then p + 1 . Unfortunately, the proof uses a "heavy" theory, so there will not even be hints here.
Usually, however, radicals will be obtained. For example, for d = 15 :
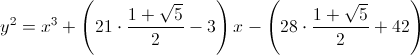. If 4p decomposes into a sum a ' 2 + d ∙ b' 2 and p is mutually simple with d , then all radicals are necessarily extracted (for example, for d = 15 there is necessarily a residue c , for which c 2 = 5̅ ) and we get an elliptic curve with the required number of points.Source: https://habr.com/ru/post/189618/
All Articles