So you still don't understand Hindley-Milner? Part 3
In Part 2, we ended up with the definitions of all formal terms and symbols that you can see in the StackOverflow question about the Hindley-Milner algorithm. So now we are ready to translate what is being asked about there, namely, the rules for deriving assertions about type inference. Let's get started!
[Var]

This translates as follows: if "
')
[App]

This translates as: if we can infer that
[Abs]
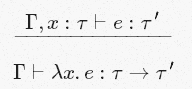
This translates as follows: if we can assume that
is of type
To the side. I have already mentioned the polytypes. Let's return to them in this example, just to make this concept better in our head. So, you have already noticed that the function above is of type
[Let]
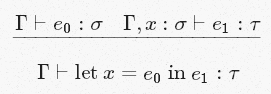
Generally easy:
If we can infer that
and
If we assume that
that
We can conclude that the result of setting
The last four rules are nothing more than a formal display of our intuitive knowledge of what type of result we can get if we have variables with which we create anonymous functions, or to which we use ordinary functions, or substitute expressions inside expressions. This is what we, as programmers, do intuitively. Here we are just talking about how to describe all this formally. In the end, not everything that happens in our brains is unknown magic. It is also worth noting that the last four rules correspond exactly to the four rules that determine what is a valid expression in lambda calculus. And this is no coincidence.
[Inst]

This is a rule about instances. You can think of the

Thus, the direct translation of [Inst] is as follows: if we can deduce that
[Gen]
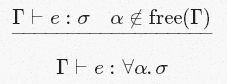
This is the most difficult part to understand. Truly, only it matters in the context of the type inference process using the narrow set of rules outlined above. It does not have a clear analogue, since it largely depends on the concept of a type variable - something that is never found in real programming languages, but is indispensable when we try to work with a meta-language to talk about types in any arbitrary programming language. In general, the idea can be shown in the following "example":
Suppose you have two variables
Since α is a type variable, i.e. can denote any type, then we would like to think that since we deduced that
And now (finally!) Translation of the rule:
If some variable of type α is not “loosely” mentioned in our current context / knowledge set / assumptions, and we can infer that some expression
Okay, but what does "loosely mentioned" mean? In the polytype ∀α.α → α, α is not mentioned "for real". This type is completely analogous, for example, ∀β.β → β. An expression with any of these types is a regular function that has the same input and output types. On the other hand,
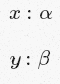
and

mean different things. The latter suggests that
That's all.
Translator's note: I would be very grateful for any comments in PM about the translation.
Rules for deriving type inference statements
[Var]

This translates as follows: if "
x has type σ" is a position from our collection of Γ positions, then from Γ you can infer that x has type σ. Here x is a variable (hence the name of the rule). Yes, it sounds painfully obvious, but it contains deep and complex facts in a concise and concise form that the machine can understand. This allows you to automate type inference.')
[App]

This translates as: if we can infer that
e 0 is an expression with the type τ → τ ′ (i.e., e 0 can be an anonymous function that, according to Γ, accepts a value of the type τ and returns the value of τ ′ ), and that e 1 is of type τ , then we can conclude that e 0 ( e 1 ), an expression obtained by applying e 0 to e 1 , is of type τ ′ . Intuitively clear: if we can infer the type of input and output function, as well as the fact that some expression has the same type as the input, then when we apply the function to this expression, we can safely conclude that the resultant the expression will have a function exit type. Nothing confusing here.[Abs]
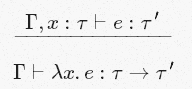
This translates as follows: if we can assume that
x is of type τ , and e is of type τ ′ , then we can conclude that we are also able to deduce the type of abstraction / anonymization e with respect to the variable x - λx.e It will be τ → τ ′ . That is, for example, if we know that the type x is a String , then the expression x[0] will be of type Char . Now [Abs] allows us to conclude that: function(x) { return x[0]; } is of type
String → Char .To the side. I have already mentioned the polytypes. Let's return to them in this example, just to make this concept better in our head. So, you have already noticed that the function above is of type
Array[Int] → Int . In fact, for any type t function is of type Array[t] → t . So actually it has many different types, and String → Char is just one of them. Each of the types of the form Array[t] → t is a monotype. We can infer that a given function has all these monotypes, simply saying that it has a polytype ∀ t(Array[t] → t) . It reads: “for any t - the type of Array[t] → t ”, and we denote a bunch of everything with a single type (but more abstract). So note that when we infer the type of an expression, this does not mean that it is unique to this expression. It can have many different types, some of which will be more specialized, while others will be more abstract. The simplest types of types are monotypes: Int , String , String → Char and the like, but if we want, we can have more abstract / common types - polytypes.[Let]
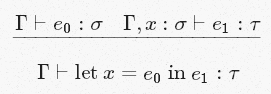
Generally easy:
If we can infer that
e 0 is of type σand
If we assume that
x also has type σ and from this we can infer that e 1 has type τthat
We can conclude that the result of setting
x to e 0 and substituting it into e 1 will be of type τ .The last four rules are nothing more than a formal display of our intuitive knowledge of what type of result we can get if we have variables with which we create anonymous functions, or to which we use ordinary functions, or substitute expressions inside expressions. This is what we, as programmers, do intuitively. Here we are just talking about how to describe all this formally. In the end, not everything that happens in our brains is unknown magic. It is also worth noting that the last four rules correspond exactly to the four rules that determine what is a valid expression in lambda calculus. And this is no coincidence.
[Inst]

This is a rule about instances. You can think of the
Array[Int] → Int monotype as an instance of the polytype ∀ t.Array[t] → t . In other words, this is “specialization”: Array[Int] → Int more specialized than ∀ t.Array[t] → t . We denote “more specialized than” with ⊑. Those.
Thus, the direct translation of [Inst] is as follows: if we can deduce that
e is of type σ ′ and σ is an instance / specialization of σ ′, then we can conclude that e is of type σ. You can think of σ and σ ′ as Array[t] → t and ∀ t.Array[t] → t respectively.[Gen]
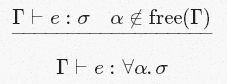
This is the most difficult part to understand. Truly, only it matters in the context of the type inference process using the narrow set of rules outlined above. It does not have a clear analogue, since it largely depends on the concept of a type variable - something that is never found in real programming languages, but is indispensable when we try to work with a meta-language to talk about types in any arbitrary programming language. In general, the idea can be shown in the following "example":
Suppose you have two variables
x and y , and in the beginning you assume that both of them are of type α, where α is a variable denoting type. Later you come across an expression for which you somehow deduced that its type is α → α in this context (in the context of the assumption that x and y are of type α). And now attention is the question: will this function have a polytype ∀α.α → α? Those. Does this function generally associate objects with the same type, or does it only seem so because you assumed that x and y have the same type α?Since α is a type variable, i.e. can denote any type, then we would like to think that since we deduced that
e is of type α → α, then it also has a polytype ∀α.α → α. But we cannot say that this generalization is obligatory, without a more complete understanding of how e is related to x and y . In particular, if our conclusion that it is of type α → α is strongly related to our previous assumptions associated with this type, then we generally cannot conclude that e has a polytype ∀α.α → α.And now (finally!) Translation of the rule:
If some variable of type α is not “loosely” mentioned in our current context / knowledge set / assumptions, and we can infer that some expression
e has some type σ, then we can conclude that e has type σ regardless of than ultimately turn α. Slightly more technical: e has the polytype ∀α.σ.Okay, but what does "loosely mentioned" mean? In the polytype ∀α.α → α, α is not mentioned "for real". This type is completely analogous, for example, ∀β.β → β. An expression with any of these types is a regular function that has the same input and output types. On the other hand,
x: α is the “real” mention of α.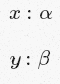
and

mean different things. The latter suggests that
x and y definitely of the same type (even if this type has not yet been defined). The first one does not report about the connection of types x and y absolutely nothing. The difference is that when α is mentioned inside the region ∀ (as in the case of ∀α.α → α), it is just a fiction that can be replaced with any other type variable, regardless of the rest of the context. Thus, we can interpret the position “α is not freely mentioned in the context of Γ” as “α either not mentioned at all, or considered fiction and in principle can be replaced by something completely different without changing the semantics of knowledge / assumptions in our context”.That's all.
Translator's note: I would be very grateful for any comments in PM about the translation.
Source: https://habr.com/ru/post/189446/
All Articles