Excel Turing Machine
The article briefly describes the Turing machine and provides its implementation on Excel. The article will be useful for those who want to get acquainted with the Turing machine, and those who want to increase their horizons in the functionality of Excel.
The Turing machine is an endless ribbon with cells. Each cell contains one character. In particular, an empty cell is a cell with the symbol of an empty cell written in it. The characters in the cells belong to the alphabet of this machine.
On the tape goes head, which can be in several states, and one of the states - the end of the machine. The head reads the current cell and, depending on the value of this cell and its current state, changes the value in the current cell, and then either moves to the right, or moves to the left, or remains in place.
To start the machine you need to specify the initial state of the tape, the state of the head and the position of the head. And, naturally, the alphabet of the machine, the state of the head and the rule must be defined.
Total rules for the head should be determined N = (number of characters in the alphabet) * (number of states -1). The number of states is 1, since there are no rules for the final state — the machine stops.
For such a machine, you need an alphabet of three characters (0.1, x) - where 0 and 1 will be for the number, and x for the empty cell. That is, the blank tape is all filled with "x" characters.
The head will have 4 states: q1, q2, q3 and q4 - machine stop.
We will write out the rules for the car in the form of a matrix:
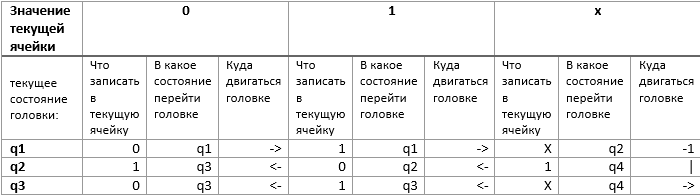
It is easy to verify that such a machine, when the head is placed on the high-order bit of a binary number, in the initial state q1, will increase this number by 1.
')
Create a table of rules, as in the example above. Select the entire table and call it “rules”. Click Enter.
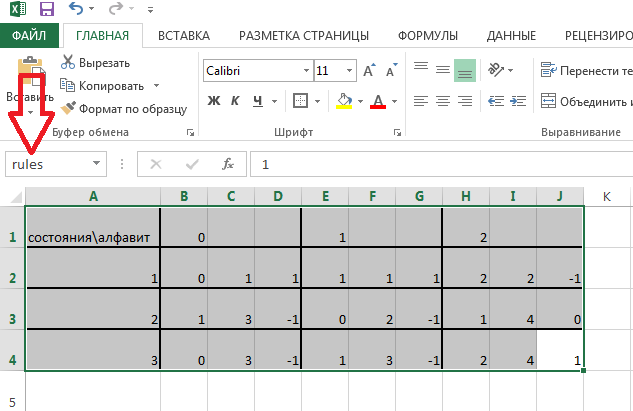
The structure of the table is the same as in the example above, with minor changes:
• machine states are called simply numbers (without q)
• an empty cell means the symbol "2"
• head movement set to 1 - right, -1 - left, 0 - in place
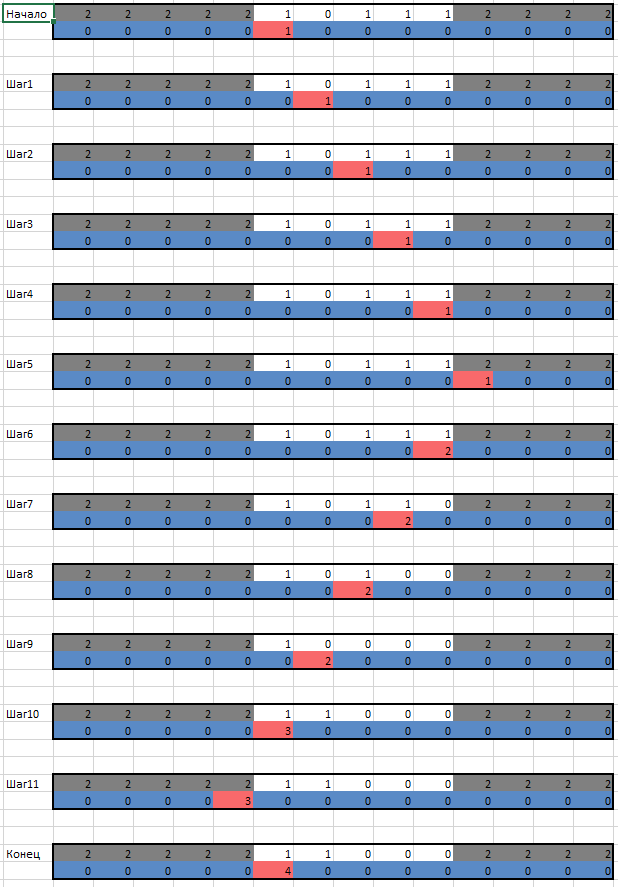
Set the initial state of the tape:

It means that the number 10111 is written on the tape, and the head is in state 1, and in the cell corresponding to the most significant digit. Excel supports conditional formatting, which is used for greater clarity.
The new machine pitch will be modeled by new Excel lines, and the formulas will simulate the state of the machine according to the rules.
Relative formulas - that is, when copying them to new cells, Excel takes data from cells corresponding to the previous state of the machine.
As a result, after completing all the steps, the machine “stops” - the state “4” is reached, one is added to the number.
Here is a link to the Excel file
If Excel would support an arbitrarily large number of rows and columns, this would automatically mean that using Excel’s formulas you can implement any computable function, since Excel would be Turing-complete
PS Problem on sharpness: change the rules of the Turing machine described in the article so that it reduces the binary number by 1.
What is a Turing Machine?
The Turing machine is an endless ribbon with cells. Each cell contains one character. In particular, an empty cell is a cell with the symbol of an empty cell written in it. The characters in the cells belong to the alphabet of this machine.
On the tape goes head, which can be in several states, and one of the states - the end of the machine. The head reads the current cell and, depending on the value of this cell and its current state, changes the value in the current cell, and then either moves to the right, or moves to the left, or remains in place.
To start the machine you need to specify the initial state of the tape, the state of the head and the position of the head. And, naturally, the alphabet of the machine, the state of the head and the rule must be defined.
Total rules for the head should be determined N = (number of characters in the alphabet) * (number of states -1). The number of states is 1, since there are no rules for the final state — the machine stops.
A simple example: adding one to a binary number
For such a machine, you need an alphabet of three characters (0.1, x) - where 0 and 1 will be for the number, and x for the empty cell. That is, the blank tape is all filled with "x" characters.
The head will have 4 states: q1, q2, q3 and q4 - machine stop.
We will write out the rules for the car in the form of a matrix:

It is easy to verify that such a machine, when the head is placed on the high-order bit of a binary number, in the initial state q1, will increase this number by 1.
')
Excel implementation
Create a table of rules, as in the example above. Select the entire table and call it “rules”. Click Enter.

The structure of the table is the same as in the example above, with minor changes:
• machine states are called simply numbers (without q)
• an empty cell means the symbol "2"
• head movement set to 1 - right, -1 - left, 0 - in place
Set the initial state of the tape:

It means that the number 10111 is written on the tape, and the head is in state 1, and in the cell corresponding to the most significant digit. Excel supports conditional formatting, which is used for greater clarity.
The new machine pitch will be modeled by new Excel lines, and the formulas will simulate the state of the machine according to the rules.
Description of Excel Formulas for the Turing Machine
Formula for tape cell:
= IF (K14 <> 0; INDEX (rules; K14 + 1; 2 + K13 * 3); K13)
This formula is for the tape cell value in the next step (K17). It means that if the head (K14) is under the cell (that is, K14 is not zero), then the value should be written to this cell according to the rules (from the rules array). If there is zero in the cell under the ribbon cell (which means there is no head under it), then the value does not change.
The formula for the state of the head (line breaks are made for readability):
= IF (K14 <> 0; IF (INDEX (rules; K14 + 1; 4 + K13 * 3) = 0; INDEX (rules; K14 + 1; 3 + K13 * 3); 0);
IF (J14 <> 0; IF (INDEX (rules; J14 + 1; 4 + J13 * 3) = 1; INDEX (rules; J14 + 1; 3 + J13 * 3); 0);
IF (L14 <> 0; IF (INDEX (rules; L14 + 1; 4 + L13 * 3) = - 1; INDEX (rules; L14 + 1; 3 + L13 * 3); 0); 0)))
This formula
1) first checks whether the head is in this cell (K14) - then if the rules are told to stay in place, the state of the machine is written in this cell according to the rules
2) If the head is one cell to the left (J14) and the rules say move to the right - then the state of the machine is written to this cell according to the rules
3) If the head is one cell to the right (L14) and the rules are said to move to the left - then the state of the machine is written to this cell according to the rules
4) In all other cases, a zero is written.
This formula simulates the movement of the head.
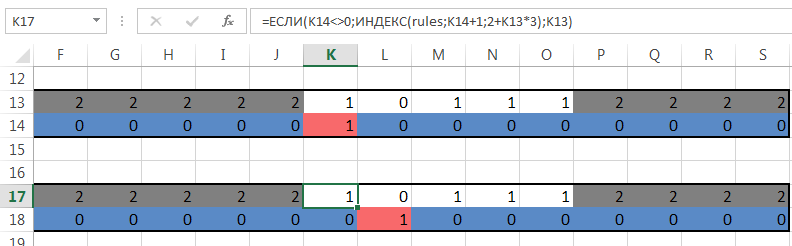
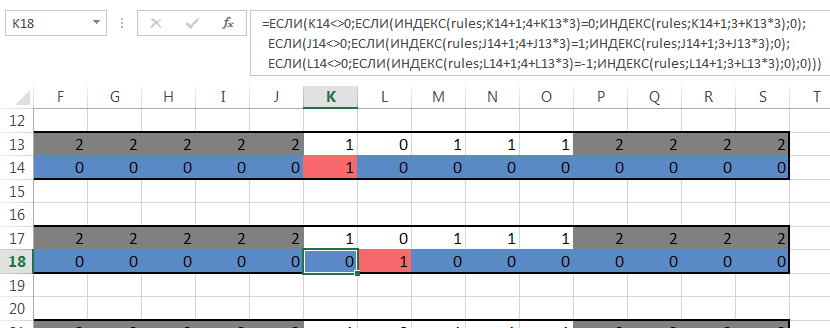
The formula uses the Index function ( array, row, column ). Calculate the value of INDEX (rules; K14 + 1; 4 + K13 * 3) - a piece of the formula for the state of the head.
As can be seen from the figure, K14 = 1, K13 = 1. So you need to find the INDEX (rules; 1 + 1; 4 + 1 * 3), that is, the INDEX (rules; 2; 7) - the value in the “rules” array at the intersection of the 2nd row and the 7th column (rows and columns starting with 1 are numbered not 0). In our plate this value is “1”.
= IF (K14 <> 0; INDEX (rules; K14 + 1; 2 + K13 * 3); K13)
This formula is for the tape cell value in the next step (K17). It means that if the head (K14) is under the cell (that is, K14 is not zero), then the value should be written to this cell according to the rules (from the rules array). If there is zero in the cell under the ribbon cell (which means there is no head under it), then the value does not change.

The formula for the state of the head (line breaks are made for readability):
= IF (K14 <> 0; IF (INDEX (rules; K14 + 1; 4 + K13 * 3) = 0; INDEX (rules; K14 + 1; 3 + K13 * 3); 0);
IF (J14 <> 0; IF (INDEX (rules; J14 + 1; 4 + J13 * 3) = 1; INDEX (rules; J14 + 1; 3 + J13 * 3); 0);
IF (L14 <> 0; IF (INDEX (rules; L14 + 1; 4 + L13 * 3) = - 1; INDEX (rules; L14 + 1; 3 + L13 * 3); 0); 0)))
This formula
1) first checks whether the head is in this cell (K14) - then if the rules are told to stay in place, the state of the machine is written in this cell according to the rules
2) If the head is one cell to the left (J14) and the rules say move to the right - then the state of the machine is written to this cell according to the rules
3) If the head is one cell to the right (L14) and the rules are said to move to the left - then the state of the machine is written to this cell according to the rules
4) In all other cases, a zero is written.
This formula simulates the movement of the head.
The formula uses the Index function ( array, row, column ). Calculate the value of INDEX (rules; K14 + 1; 4 + K13 * 3) - a piece of the formula for the state of the head.
As can be seen from the figure, K14 = 1, K13 = 1. So you need to find the INDEX (rules; 1 + 1; 4 + 1 * 3), that is, the INDEX (rules; 2; 7) - the value in the “rules” array at the intersection of the 2nd row and the 7th column (rows and columns starting with 1 are numbered not 0). In our plate this value is “1”.

Relative formulas - that is, when copying them to new cells, Excel takes data from cells corresponding to the previous state of the machine.
As a result, after completing all the steps, the machine “stops” - the state “4” is reached, one is added to the number.

Here is a link to the Excel file
Conclusion
If Excel would support an arbitrarily large number of rows and columns, this would automatically mean that using Excel’s formulas you can implement any computable function, since Excel would be Turing-complete
PS Problem on sharpness: change the rules of the Turing machine described in the article so that it reduces the binary number by 1.
Source: https://habr.com/ru/post/189064/
All Articles