Probabilistic models: struggle with cycles and variational approximations
In the fourth series of the cycle about graphical probabilistic models ( part 1 , part 2 , part 3 ) we will continue to talk about how to cope with complex factor graphs. Last time we studied the message transfer algorithm, which, however, works only in cases where the factor graph is a tree, and at each node you can easily recalculate the distribution by brute force. What to do in really interesting cases, when there are large informative cycles in the graph, we will start discussing today - let's talk about a couple of relatively simple methods and discuss a very powerful, but difficult to use tool - variational approximations.

First, let us recall what a factor graph, which we discussed last time. This is a bichromatic graph in which two types of vertices correspond to variables and functions. Each function is associated with those variables on which it depends, and the graph itself defines the decomposition of a large function into a product of small ones. Last time we examined in detail a very simple example of a factor graph - a linear chain of nodes
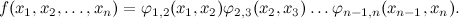 ,
,
which corresponds to decomposition

')
The message passing algorithm, the essence of which we saw in this example, works almost unchanged in any factor graph, which is a tree: messages are transmitted from the leaves to the tree, converge at the root of the tree (which can be any node), and then diverge back . As a result, each vertex of the graph receives messages from all its neighbors, after which it can easily calculate the sum of the original expansion for all variables except itself (thereby calculating its own marginal distribution).
However, in real life, not all useful probabilistic models are described by tree graphs. We have already considered one such example in our series of articles - this is the LDA model (latent Dirichlet allocation), which is very useful for automatic text analysis and looks like this in the Bayesian network:

Let me remind you that the model shown in this picture generates a new document of length N as follows:
The picture looks so simple because it uses so-called “plates” (plates) - each rectangle actually implies several copies of everything that is depicted in it. For example, if you fully draw the LDA factor graph, say, for two documents, one of which has two words, and three in another, already at this stage you get a rather impressive structure (in order not to overload the picture completely, I did not sign the functions):

As you can see, there are a lot of cycles here, and they come from the fact that the same parameters α and β are used repeatedly to obtain different observations. This situation, of course, occurs very often - in fact, this is the main formulation of tasks in machine learning: assuming that the distribution parameters are the same, evaluate them or predict subsequent observations. Therefore, cycles in graphic models are not a bug, but a feature. And we will now try to talk about how to implement this feature. Immediately I warn you that our narrative is gradually entering more and more mathematically complex areas; today I will be waving my hands more than proving something, and then we will go on to concrete examples. For those who wish to study the material, I recommend to see Bishop’s excellent book on Bayesian output , Hastie et al. about machine learning , course on graphic models on Coursera and other sources - nowadays there is no shortage of sources.
And we will slowly cope with cycles. Today I will look at several methods that allow you to cope with cycles in some cases, and when they work, it is usually more convenient and computationally easier to use and use. And another time we will talk about a more general method related to Gibbs sampling (more precisely, sampling based on Markov chains - Markov chain Monte Carlo).
Sometimes a cycle can be painlessly replaced by one vertex, simply by increasing the number of variables of the corresponding function. For example, you got a triangle somewhere in the factor graph:

As we already know, it means that in decomposition occurs

In most cases, such a triangle can be safely replaced by a new function.

and the cycle will disappear:

The disadvantage of this method is clear - as the number of arguments increases, the calculation function, as a rule, grows exponentially (if they do not grow, then the task of marginalizing does not pose much difficulty, so there is no need to fence a garden with graphic models). Therefore, you can only cope with small cycles. And in practically important tasks, the cycles are often very large, passing through the entire diameter of the graph: look at least at the cycles in the LDA model, passing from α to β and back. Therefore, this “toy” method, in reality, as a rule, is not applicable - more precisely, the models are usually immediately built as if it had already been used in all possible cases.
The first practically important method that can be used if the message transfer algorithm is not applicable is, of course, a message transfer algorithm. :) Of course, for cycles it, formally speaking, does not work - there is no place to start, no leaves. Therefore, a modification of the message passing algorithm, known as loopy belief propagation, is used here:
Of course, such a mockery of the message passing algorithm is not completely painless. First, it becomes approximate from the exact; if earlier it was enough to drive the messages along each edge once in each direction, now the messages are sent immediately along all edges and gradually change; we hope that over time these messages will stop changing (converge on some values), and then we take these values as an answer.
Secondly, even this hope is not always justified. It is easy to build an example in which the message passing algorithm cannot converge anywhere — for example, it can oscillate between two fixed states (let's leave it as an exercise for the reader, building such an example is not very difficult). On the other hand, he may still converge, but converge to the wrong answer (here non-trivial examples are more technically complex, let me give you the word of a gentleman that they exist). However, there are a number of works in which the conditions are given under which the loopy belief propagation converges where necessary; these conditions are often met, and even when they are not met, the algorithm often works in practice as it should.
I will note here for the future: loopy belief propagation looks very similar to the Gibbs sampling, which we will do next time; However, in reality there is a fundamental difference between the methods. The main difference lies in the fact that loopy belief propagation is a deterministic algorithm, and if you are not lucky with it, then nothing will be done. And the sampling methods are fundamentally randomized, and even if one of the sampler launches leads to incorrect results, in most other launches the case is likely to improve. But more about that later.
The last method of dealing with overly complex models, which I wanted to talk about today, is variational approximations. Most likely, if you have a physical or mathematical education, you understand better than me what a variational approximation is; but I still try to explain on the fingers. The essence of the method is as follows: we are trying to add new degrees of freedom to the original problem and present it as an optimization problem (for new, artificially introduced parameters).
To understand what all this means in general, let us consider the classic simplest example — let us present the logarithm function in variational form:

(this equality is easy to check, just taking the derivative with respect to λ - check!).
Now this is a family of linear functions, each of which gives an upper estimate for the logarithm (in other words, the logarithm is the envelope of this family), and if we succeed in choosing λ well, then we get good estimates in the region of interest. It looks like this (picture from the article [ Jordan et al., 1999 ]):

It was very important that the logarithm is a concave function, otherwise it would not work. But often you can achieve the properties of the bulge in a different way. The second example is the logistic function:

It is not convex or concave, but it is log-concave, i.e.

is a concave function of x . Therefore, for g ( x ) one can find linear estimates:

Where i.e. ordinary entropy. Again, exercise - check it out (something a bit too much exercise today, but what to do). Then you can take the exponent (it is monotonous, ie, the inequality will remain):
i.e. ordinary entropy. Again, exercise - check it out (something a bit too much exercise today, but what to do). Then you can take the exponent (it is monotonous, ie, the inequality will remain):

In particular, we obtain a family of upper bounds:

and the better we choose λ, the better we estimate. Graphically, it looks like this (image from [ Jordan et al., 1999 ]):

What does the graphic model? But with what. Let me remind you that we are dealing with the problem of marginalization: using this model and, possibly, the values of some variables, find the marginal probability distribution

where X and Y are subsets of variables (usually Y is a small subset, often one variable of interest). Let us not summarize the joint distribution in the forehead (in particular, when we draw a factor graph, it turns out many cycles). If we can find variational estimates for the joint distribution, we get an estimate

where λ - variation parameters. Here it is assumed that we, of course, were not fools and chose them specifically so that now the summation was easy to carry out. Then the result is a function of a relatively small number of variables, Y and λ, and the initial task of marginalization turns into the problem of minimizing this function with respect to λ, which is often much easier to do.
If we look at everything that happens from a slightly different angle, then the essence of the variational approximations can be represented as follows:
There are two minuses here: first, the answer is approximate, because even with a good solution of the optimization problem, variational estimates do not always relate so successfully to the desired function, as in the pictures above, sometimes there is a gap (that is, the class of simple distributions is noticeably separated from the desired complex distribution). But it is not so bad, no one expects an exact solution in difficult cases. The more important problem is that variation methods are always a “manual” solution; you cannot automate them: you need to find a successful form of variation variation, which is easily summed up and which can then be optimized. Such forms were found for some classes of models, but in general for every serious modification the scientific search begins anew (although, of course, not from scratch).
So, for example, in the developed scheme of the variation approximation for the LDA model, the graphical model from the one shown above (in the first section of the article) turns into this (picture from the article [ Blei, Jordan, Ng, 2003 ]):

As you can see, there are no longer any cycles left, and the problem of marginalization has received an approximate solution, which is reduced to an optimization problem with respect to the variational parameters γ and φ.
However, for LDA there is a fairly simple Gibbs sampling scheme; the difference here is that Gibbs sampling is in this case a very simple and straightforward method, it is easy to understand and program (more precisely, it is easy to understand how it works, and that’s why it works is a slightly more subtle question), and the variational method is more complicated, but the algorithm is more efficient as a result. As a result, as a rule, articles on various extensions of LDA are divided into two classes: if the authors manage to find a variational approximation, they give the scheme of such an approximation and the corresponding inference algorithm; if not, they are limited by the Gibbs sampling scheme, which, as a rule, is more or less automatic for any extensions.
Next time, we will continue our acquaintance with inference methods in complex probabilistic models and talk about sampling, which is currently the most versatile tool for approximate inference.

Summary of the previous series
First, let us recall what a factor graph, which we discussed last time. This is a bichromatic graph in which two types of vertices correspond to variables and functions. Each function is associated with those variables on which it depends, and the graph itself defines the decomposition of a large function into a product of small ones. Last time we examined in detail a very simple example of a factor graph - a linear chain of nodes
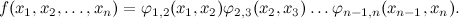 ,
,which corresponds to decomposition

')
The message passing algorithm, the essence of which we saw in this example, works almost unchanged in any factor graph, which is a tree: messages are transmitted from the leaves to the tree, converge at the root of the tree (which can be any node), and then diverge back . As a result, each vertex of the graph receives messages from all its neighbors, after which it can easily calculate the sum of the original expansion for all variables except itself (thereby calculating its own marginal distribution).
However, in real life, not all useful probabilistic models are described by tree graphs. We have already considered one such example in our series of articles - this is the LDA model (latent Dirichlet allocation), which is very useful for automatic text analysis and looks like this in the Bayesian network:

Let me remind you that the model shown in this picture generates a new document of length N as follows:
- choose vector
 - vector "degree of expression" of each topic in the document;
- vector "degree of expression" of each topic in the document; - for each of the N words w :
- choose a topic
 by distribution
by distribution  ;
; - choose a word
 with probabilities given in β.
with probabilities given in β.
- choose a topic
The picture looks so simple because it uses so-called “plates” (plates) - each rectangle actually implies several copies of everything that is depicted in it. For example, if you fully draw the LDA factor graph, say, for two documents, one of which has two words, and three in another, already at this stage you get a rather impressive structure (in order not to overload the picture completely, I did not sign the functions):

As you can see, there are a lot of cycles here, and they come from the fact that the same parameters α and β are used repeatedly to obtain different observations. This situation, of course, occurs very often - in fact, this is the main formulation of tasks in machine learning: assuming that the distribution parameters are the same, evaluate them or predict subsequent observations. Therefore, cycles in graphic models are not a bug, but a feature. And we will now try to talk about how to implement this feature. Immediately I warn you that our narrative is gradually entering more and more mathematically complex areas; today I will be waving my hands more than proving something, and then we will go on to concrete examples. For those who wish to study the material, I recommend to see Bishop’s excellent book on Bayesian output , Hastie et al. about machine learning , course on graphic models on Coursera and other sources - nowadays there is no shortage of sources.
And we will slowly cope with cycles. Today I will look at several methods that allow you to cope with cycles in some cases, and when they work, it is usually more convenient and computationally easier to use and use. And another time we will talk about a more general method related to Gibbs sampling (more precisely, sampling based on Markov chains - Markov chain Monte Carlo).
Replace loop to the top
Sometimes a cycle can be painlessly replaced by one vertex, simply by increasing the number of variables of the corresponding function. For example, you got a triangle somewhere in the factor graph:

As we already know, it means that in decomposition occurs

In most cases, such a triangle can be safely replaced by a new function.

and the cycle will disappear:

The disadvantage of this method is clear - as the number of arguments increases, the calculation function, as a rule, grows exponentially (if they do not grow, then the task of marginalizing does not pose much difficulty, so there is no need to fence a garden with graphic models). Therefore, you can only cope with small cycles. And in practically important tasks, the cycles are often very large, passing through the entire diameter of the graph: look at least at the cycles in the LDA model, passing from α to β and back. Therefore, this “toy” method, in reality, as a rule, is not applicable - more precisely, the models are usually immediately built as if it had already been used in all possible cases.
Message Transfer Algorithm
The first practically important method that can be used if the message transfer algorithm is not applicable is, of course, a message transfer algorithm. :) Of course, for cycles it, formally speaking, does not work - there is no place to start, no leaves. Therefore, a modification of the message passing algorithm, known as loopy belief propagation, is used here:
- send from each vertex variable to each vertex function a message that is identically equal to 1;
- continue to use the usual message passing algorithm.
Of course, such a mockery of the message passing algorithm is not completely painless. First, it becomes approximate from the exact; if earlier it was enough to drive the messages along each edge once in each direction, now the messages are sent immediately along all edges and gradually change; we hope that over time these messages will stop changing (converge on some values), and then we take these values as an answer.
Secondly, even this hope is not always justified. It is easy to build an example in which the message passing algorithm cannot converge anywhere — for example, it can oscillate between two fixed states (let's leave it as an exercise for the reader, building such an example is not very difficult). On the other hand, he may still converge, but converge to the wrong answer (here non-trivial examples are more technically complex, let me give you the word of a gentleman that they exist). However, there are a number of works in which the conditions are given under which the loopy belief propagation converges where necessary; these conditions are often met, and even when they are not met, the algorithm often works in practice as it should.
I will note here for the future: loopy belief propagation looks very similar to the Gibbs sampling, which we will do next time; However, in reality there is a fundamental difference between the methods. The main difference lies in the fact that loopy belief propagation is a deterministic algorithm, and if you are not lucky with it, then nothing will be done. And the sampling methods are fundamentally randomized, and even if one of the sampler launches leads to incorrect results, in most other launches the case is likely to improve. But more about that later.
Variational approximations
The last method of dealing with overly complex models, which I wanted to talk about today, is variational approximations. Most likely, if you have a physical or mathematical education, you understand better than me what a variational approximation is; but I still try to explain on the fingers. The essence of the method is as follows: we are trying to add new degrees of freedom to the original problem and present it as an optimization problem (for new, artificially introduced parameters).
To understand what all this means in general, let us consider the classic simplest example — let us present the logarithm function in variational form:

(this equality is easy to check, just taking the derivative with respect to λ - check!).
Now this is a family of linear functions, each of which gives an upper estimate for the logarithm (in other words, the logarithm is the envelope of this family), and if we succeed in choosing λ well, then we get good estimates in the region of interest. It looks like this (picture from the article [ Jordan et al., 1999 ]):

It was very important that the logarithm is a concave function, otherwise it would not work. But often you can achieve the properties of the bulge in a different way. The second example is the logistic function:

It is not convex or concave, but it is log-concave, i.e.

is a concave function of x . Therefore, for g ( x ) one can find linear estimates:

Where
 i.e. ordinary entropy. Again, exercise - check it out (something a bit too much exercise today, but what to do). Then you can take the exponent (it is monotonous, ie, the inequality will remain):
i.e. ordinary entropy. Again, exercise - check it out (something a bit too much exercise today, but what to do). Then you can take the exponent (it is monotonous, ie, the inequality will remain):
In particular, we obtain a family of upper bounds:

and the better we choose λ, the better we estimate. Graphically, it looks like this (image from [ Jordan et al., 1999 ]):

What does the graphic model? But with what. Let me remind you that we are dealing with the problem of marginalization: using this model and, possibly, the values of some variables, find the marginal probability distribution

where X and Y are subsets of variables (usually Y is a small subset, often one variable of interest). Let us not summarize the joint distribution in the forehead (in particular, when we draw a factor graph, it turns out many cycles). If we can find variational estimates for the joint distribution, we get an estimate

where λ - variation parameters. Here it is assumed that we, of course, were not fools and chose them specifically so that now the summation was easy to carry out. Then the result is a function of a relatively small number of variables, Y and λ, and the initial task of marginalization turns into the problem of minimizing this function with respect to λ, which is often much easier to do.
If we look at everything that happens from a slightly different angle, then the essence of the variational approximations can be represented as follows:
- we have a complex distribution, which is not clear what to do;
- we find a class of simple distributions with which it is easy and pleasant to live;
- and then we try in this class to find a distribution that is most similar to our original complex distribution (optimizing by variational parameters).
There are two minuses here: first, the answer is approximate, because even with a good solution of the optimization problem, variational estimates do not always relate so successfully to the desired function, as in the pictures above, sometimes there is a gap (that is, the class of simple distributions is noticeably separated from the desired complex distribution). But it is not so bad, no one expects an exact solution in difficult cases. The more important problem is that variation methods are always a “manual” solution; you cannot automate them: you need to find a successful form of variation variation, which is easily summed up and which can then be optimized. Such forms were found for some classes of models, but in general for every serious modification the scientific search begins anew (although, of course, not from scratch).
So, for example, in the developed scheme of the variation approximation for the LDA model, the graphical model from the one shown above (in the first section of the article) turns into this (picture from the article [ Blei, Jordan, Ng, 2003 ]):

As you can see, there are no longer any cycles left, and the problem of marginalization has received an approximate solution, which is reduced to an optimization problem with respect to the variational parameters γ and φ.
However, for LDA there is a fairly simple Gibbs sampling scheme; the difference here is that Gibbs sampling is in this case a very simple and straightforward method, it is easy to understand and program (more precisely, it is easy to understand how it works, and that’s why it works is a slightly more subtle question), and the variational method is more complicated, but the algorithm is more efficient as a result. As a result, as a rule, articles on various extensions of LDA are divided into two classes: if the authors manage to find a variational approximation, they give the scheme of such an approximation and the corresponding inference algorithm; if not, they are limited by the Gibbs sampling scheme, which, as a rule, is more or less automatic for any extensions.
Next time, we will continue our acquaintance with inference methods in complex probabilistic models and talk about sampling, which is currently the most versatile tool for approximate inference.
Source: https://habr.com/ru/post/188812/
All Articles