Handwriting recognition

Introduction

This article will discuss the method of handwriting recognition by analyzing all points of the plane and looking through all possible combinations in order to find the best imposition of control points on the previously described figures. I will explain.
Handwriting input is drawing with the imaginable “pen” of a certain shape. Drawing in computer systems is the preservation in the graphic memory of information about all pixels of the graphic context. “Point on a plane” in mathematics is an abstract concept. In the same computer graphics behind this concept is "pixel". This recognition algorithm will analyze the set of points (pixels) provided to it and try to find in it the most possible and similar figure. The figure, in turn, is a frame containing only the main (control) points that make the figure unique.

Materiel

')
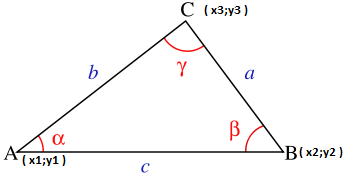
Generally speaking, the heart of the algorithm is the Cosinos Theorem , which has been well known since the school days, and is a generalized Pythagorean theorem. Knowing the coordinates of three points of the plane and their order of “appearing” on it, we can easily determine the angle described by these points (the top of the angle is the second point in a row):

A (x1; y1)
B (x2; y2)
C (x3; y3)

the distances between points are by the Pythagorean theorem

a ^ 2 = b ^ 2 + c ^ 2 - 2 * b * c * cos (ALPHA)
cos (ALPHA) = (b ^ + c ^ -a ^) / 2 * b * c

Knowing the cosine, the angle can easily be calculated.

Among the set of points that are fed to the input of the algorithm, it is necessary to “substitute” points into all possible skeletons of figures (about them above) and choose the best solution among those found. This is done as follows:

1. We take the first and last points of the frame of the figures. Already there are two, it remains to find the third (to find the angle).
2. The search for the third one is performed by enumerating all subsequent points after the first one. The decision to include a point in the proposed frame of the figure is made on the basis of two analyzes:
   
   • Attempt to substitute a point in the corner (as the third, final) and check it for compliance with the value of the same angle in the frame of the real figure.
   • Check the aspect ratio of the resulting angle with the same aspect ratio of the angle in the frame of the real figure.
   
   

If these two conditions are fulfilled, the algorithm decides on the inclusion of a point from a set of points into a conceivable framework (at the same time increasing the magnitude of the similarity to the current analyzed figure).

If, for example, we have several analyzed frames, for example, "8" and "6". And the result of the recognition algorithm: "8" -80%, "6" - 90%, then the decision is made in favor of the figure in whose frame there are more control points, that is, in favor of the eight.

The percentage of similarity of a set of points with points in the frame is calculated simply: all points that converge with the same points in the frame are added together and the relationship is found. Suppose if there are N control points in the frame, and we have agreed M, then the percentage of similarity is M / N * 100

In words, something may not be clear. Therefore, everything is the same, but clearly (for example, the number "6"):



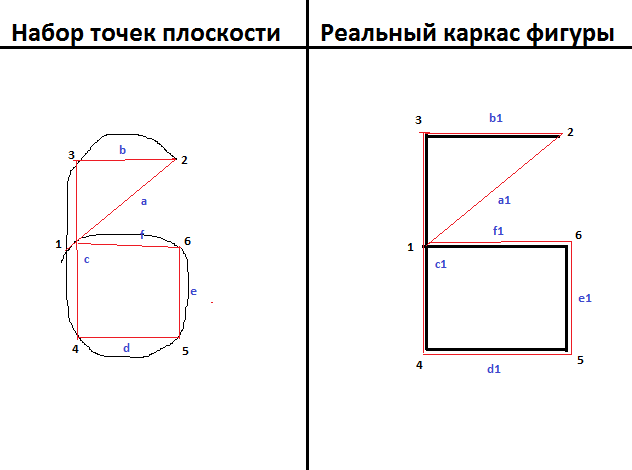
Black denotes sets of points, red - the frame, in accordance with which the analysis takes place.

The numbers indicate the points of the corners (starting from the last), if we assume that we draw the six from the point “2” and end it with the point “1”, then the first two points from which the frame analysis starts are “1” and “2”, then search point "3", so that its parameters relative to the angle formed by it coincided with the theme of the same parameters in the frame. Further, as we found the point "3", we are looking for the point "4" (already relying on the points "2" and "3") again, in accordance with the real frame, etc.

The letters indicate the sides of the corners. Ie, following the rules of the algorithm, a point from the set (points of the plane) can be included in the proposed framework if (examples):

(angle 2 ~ = corner 2 in the frame) And (a / b ~ = a1 / b1) then the point "3" will be included
(angle 3 ~ = corner 3 in the frame) AND (b / c ~ = b1 / c1) then the point "4" will be included
etc

The description of the algorithm ends here.

Code

It is easy to say, but before you say it is necessary to think carefully how to do the above ...

Well, I already thought and implemented the invented algorithm using C ++ and the OpenGL graphic library (+ GLUT add-in). A graphic library is used to draw a set of points in a two-dimensional space. The code was not so little, but not so much. Virtually all of the code is separated into C ++ header files. The project is laid out in public access for all who are interested in it at least a little. Sources are located on Bitbucket . The project uses the GIT version control system, so for those who wish to download the project source codes, this should not be a problem.

To switch to the shape programming mode, right-click in the main window. Then draw a skeleton (using points connected between each other in a series of segments) and press the middle mouse button. “Done!” Will appear on the screen. After that, restart the application.

Underwater rocks

Almost everywhere they are ... and this algorithm is no exception. Frankly, the algorithm allows for periodic misfires in correct recognition.
Take, for example, the characters "S" and "5", where misfires are almost inevitable. Although, if you qualitatively identify all control points, then, most likely, misfires can be avoided. There may also be misfires when analyzing shapes that have complex roundness. If misfires occur on dissimilar characters (I, for example, had a misfire with “6” and “8”: 6 - 100%, 8 - 83%), then you can program the frame of each of the figures again (the number of repetitions is unlimited). So it will be possible to avoid errors in recognition. And the last thing to note is the angle formed by the last, first and second points + the ratio of its sides must be remembered. To do this, you can “align” this angle to 90 degrees, as shown in the demo video below.

I only mentioned numbers in the article, as you might have noticed. But, in fact, recognition is applicable to absolutely any figures of two-dimensional space. I also made a small supplement to the article - a video demonstrating the operation of the algorithm.

If you have any questions, then ask - I will be happy to answer them.