Search for the shortest path in the transport graph (concept) + source
There was somehow a project with me that was associated with a map of the city. And the idea arose that since there is a map with routes and the corresponding stops of urban transport, then why not make a search for the route from point A to point B on it.
Since the hardware where the software was supposed to be placed has an extremely narrow Internet channel, the search would have to be fully carried out locally, that is, without involving the server’s capacity. In addition, of course, I wanted to not lose the user's attention and give him the result as soon as possible.
For about an hour or two I was sitting and could not think of anything, and then I had the idea that I could consider the route, not as a lot of stops, but as 1 point. And if I take the routes to a point, then I get a very simple graph.
The idea seemed good, and I liked it.
')
The first thing I did was stop the transport routes from sites. Then he began to count.
This turned out to be not a difficult task; we take every stop of the route and see if there are any stops of any other route in the radius we set. The radius took 600m (in the latest version 400m) - the estimated distance that a person can walk without pain on foot from one stop to another if a transfer is necessary. Probably, this distance can be reduced, say, to 200m, since the distance from one stop to another at an intersection does not exceed this distance.
So, after all these manipulations, I got a graph, along which you can quickly build a path from one route to another. Thus, we have a graph that stores information about the transitions from one urban transport route to another, a kind of meta graph.
Over several months, the algorithm has been corresponded a couple of times, then I’ll tell you in more detail about the latest implementation.
The quality of the video is terrible, but how to do better, I have not found.
The average time spent on the steps:
gpt - 0.009s, find the nearest stops to the click point
grt - 0.001s, find the shortest path from the route to the route
apt - 0.0001s, add stops and turning points to our route
all - 0.01c, the total time to perform a search path
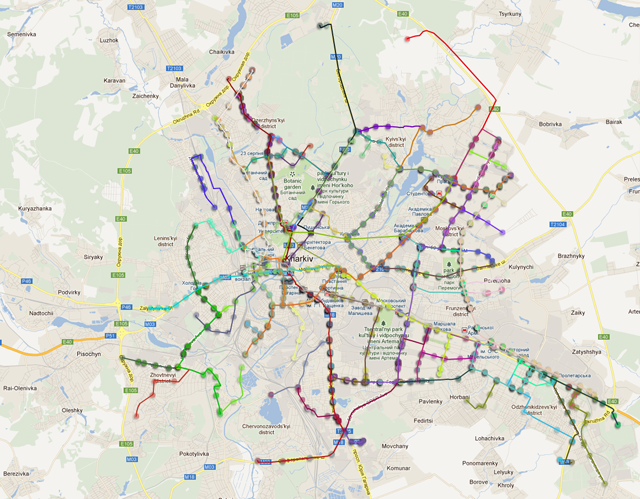
We have a certain map of the city, with the routes of urban transport marked on it (90 routes) and the coordinates of the corresponding stops belonging to these routes.
On the map, the routes look like this:
All my software implementations based on MYSQL were very slow. I decided to move away from the base. I unloaded the data into the array and decided to work through the socket. In my case, the uploaded data takes up about 19MB of RAM.
The main array is our $ graf array. This is a three-dimensional array of keys for which:
Since the stop of one route can fall between 2 stops of another or the routes adjoin at more than 1 point, we will get a lot of transfer options. So, $ v1, $ v2 are these transfers.
Also in memory is an array with distances inside the route, that is, an array of the form:
$ routeDistance [$ idRoute] [$ pFrom] [$ pTo] = (float);
Where:
To start the search we need to find a stop from where we will go and where. After we have found the nearest stops from where ($ idFrom) and where ($ idTo) to go, we have determined the belonging of the stops to the routes, we will try to find the way.
To find a path with 1 transplant:
The search for a path, for example, with 2 transplants is implemented like this:
Accordingly, in order to find a way, for example, with 3 transfers, we write as follows:
After these operations, we get a set of routes of the form $ id1 -> $ id2 -> $ id3 -> $ id4. Where $ id * is the route id.
Next, we need to understand which path is the fastest. We have a start stop ($ pStart) and a stop end ($ pEnd). Also in the $ graf table, we know the transfer points (from where, where and the distance) are our values $ v1, $ v2.
I'll sign for $ id1 -> $ id2. We add to them data on all transfers:
A bit of obvious, to evaluate the route you need to add up everything:
$ routeDistance [$ id1] [$ pStart] [$ v1 ['from']] - distance inside the route.
$ v1 ['distance'] - how much time is spent on transplantation, also in abstract units.
Accordingly, the minimum value of the calculated amounts, this will be our desired path. Next, we restore the stops that are inside the route, but are located between the point of entry into the route and the exit from it.
For convenience, we choose several routes:
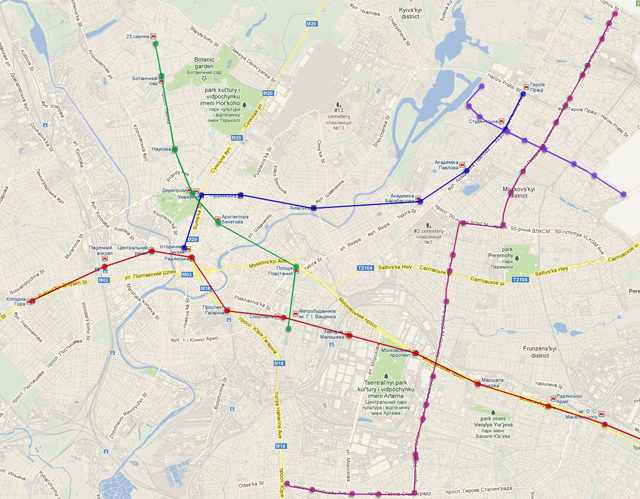
We roll up the routes to points and get the graph:

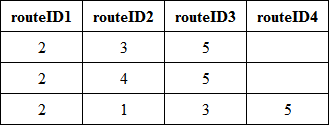
Suppose we need to go from 2 to 5 routes.
According to our graph we get this sample paths:
Further we work with the received routes. We need to know which route is the fastest.
Calculation of the value of the "attractiveness" of the route:
Take the first line of our sample.

$ routeDistance [2] [p.1] [p.3] + d1 + $ routeDistance [3] [p.5] [p.6] + d3 + $ routeDistance [5] [p.7] [p.8 ] = (float)
$ routeDistance [2] [p.1] [p.4] + d2 + $ routeDistance [3] [p.5] [p.6] + d3 + $ routeDistance [5] [p.7] [p.8 ] = (float)
$ routeDistance - the distance within the route.
d * - time to transfer.
p.1 - stop where we are going.
p.8 - stop where we are going.
d1 - the distance between p.3 and p.5
The minimum number is the best way.
- as long as the algorithm does not take into account the existing road network and does not lay a pedestrian route from point A to the transport stop and, accordingly, from the last public transport stop from the received route to point B;
- of course, you can further consider the cost of routes and, if necessary, enter the optional selection of criteria by which to choose a route (minimum cost, time, transfers, etc.), while by default we consider the target criterion to be minimum transfers;
- if they had entered fares depending on the length of the path, then also in the algorithm there would not be much to add;
Sources download . Unpack The path should not contain Russian characters.
Since the hardware where the software was supposed to be placed has an extremely narrow Internet channel, the search would have to be fully carried out locally, that is, without involving the server’s capacity. In addition, of course, I wanted to not lose the user's attention and give him the result as soon as possible.
For about an hour or two I was sitting and could not think of anything, and then I had the idea that I could consider the route, not as a lot of stops, but as 1 point. And if I take the routes to a point, then I get a very simple graph.
The idea seemed good, and I liked it.
')
The first thing I did was stop the transport routes from sites. Then he began to count.
This turned out to be not a difficult task; we take every stop of the route and see if there are any stops of any other route in the radius we set. The radius took 600m (in the latest version 400m) - the estimated distance that a person can walk without pain on foot from one stop to another if a transfer is necessary. Probably, this distance can be reduced, say, to 200m, since the distance from one stop to another at an intersection does not exceed this distance.
So, after all these manipulations, I got a graph, along which you can quickly build a path from one route to another. Thus, we have a graph that stores information about the transitions from one urban transport route to another, a kind of meta graph.
Over several months, the algorithm has been corresponded a couple of times, then I’ll tell you in more detail about the latest implementation.
The quality of the video is terrible, but how to do better, I have not found.
The average time spent on the steps:
gpt - 0.009s, find the nearest stops to the click point
grt - 0.001s, find the shortest path from the route to the route
apt - 0.0001s, add stops and turning points to our route
all - 0.01c, the total time to perform a search path
Data:
We have a certain map of the city, with the routes of urban transport marked on it (90 routes) and the coordinates of the corresponding stops belonging to these routes.
On the map, the routes look like this:

A boring description of the structure of the base
Data is presented in the following tables:
In order not to waste time every time you search for a route, it’s time to calculate the distance between stops (as part of route 1) and write it in the appropriate table.
Get the distance table:
Next, we will construct a meta-graph of transitions, that is, we will find those stops of the route, within whose radius there are stops from other routes. As already noted, I chose a radius of 400 meters.
The result of processing is written in the table:
route( id, name, color, route_type_id ) // route_type( id, name ) // - , , , , route_points( id, marker_description_id, route_id, marker_order ) // , marker( id, x, y, address ) // marker_category( id, name ) // marker_description( id, name, marker_category_id, marker_id ) In order not to waste time every time you search for a route, it’s time to calculate the distance between stops (as part of route 1) and write it in the appropriate table.
Get the distance table:
route_distance( route_id, // roite_point_from_id, // roite_point_to_id, // distance // ) Next, we will construct a meta-graph of transitions, that is, we will find those stops of the route, within whose radius there are stops from other routes. As already noted, I chose a radius of 400 meters.
The result of processing is written in the table:
route_cross_points( route_from_id, // route_to_id, // route_point_from_id, // route_point_to_id, // distance // ) //, Data upload to php
All my software implementations based on MYSQL were very slow. I decided to move away from the base. I unloaded the data into the array and decided to work through the socket. In my case, the uploaded data takes up about 19MB of RAM.
The main array is our $ graf array. This is a three-dimensional array of keys for which:
- 1st key is the route from which we are transplanted
- 2nd key that is transplanted
- 3rd transfer point
$r = $this->db->query(' select routeFrom rf, routeTo rt, markerFrom mf, markerTo mt, distance d from route_cross_points RCP '); $kf = 0; foreach($r as $k => $v) { $this->graf[(int)($v['rf'])][(int)($v['rt'])][] = array((int)($v['mf']), (int)($v['mt']), (float)($v['d'])); } $graf[$idFrom][$idTo] = array( 0 => $v1, // , 1 => $v2 // , ..... ); Since the stop of one route can fall between 2 stops of another or the routes adjoin at more than 1 point, we will get a lot of transfer options. So, $ v1, $ v2 are these transfers.
Also in memory is an array with distances inside the route, that is, an array of the form:
$ routeDistance [$ idRoute] [$ pFrom] [$ pTo] = (float);
Where:
- $ idRoute - id of our route,
- $ pFrom - stop with which to go,
- $ pTo - stop where to go,
- (float) - the value of the path in abstract units.
$rt = $this->db->query(' select route_id rni, POINT1 p1, POINT2 p2, distance d from route_distance '); foreach($rt as $k => $v) { $this->routeDistance[(int)($v['rni'])][(int)($v['p1'])][(int)($v['p2'])] = (int)($v['d']); } Finding the way
To start the search we need to find a stop from where we will go and where. After we have found the nearest stops from where ($ idFrom) and where ($ idTo) to go, we have determined the belonging of the stops to the routes, we will try to find the way.
To find a path with 1 transplant:
if(isset($graf[$idFrom][$idTo])) { // 1 . } The search for a path, for example, with 2 transplants is implemented like this:
foreach($graf[$idFrom] as $keyOne => $one) { if(isset($graf[$idTo][$keyOne])) { // , , . } } Accordingly, in order to find a way, for example, with 3 transfers, we write as follows:
foreach($graf[$idFrom] as $keyOne => $one) // { foreach($graf[$idFrom] as $keyTwo => $two)// { if(isset($graf[$keyOne][$keyTwo])){ } } } After these operations, we get a set of routes of the form $ id1 -> $ id2 -> $ id3 -> $ id4. Where $ id * is the route id.
Next, we need to understand which path is the fastest. We have a start stop ($ pStart) and a stop end ($ pEnd). Also in the $ graf table, we know the transfer points (from where, where and the distance) are our values $ v1, $ v2.
I'll sign for $ id1 -> $ id2. We add to them data on all transfers:
$id1($pStart, $v1['from']) -> $id2($v1['to'], $pEnd) $id1($pStart, $v2['from']) -> $id2($v2['to'], $pEnd) $id1($pStart, $v3['from']) -> $id2($v3['to'], $pEnd) A bit of obvious, to evaluate the route you need to add up everything:
$routeDistance[$id1][$pStart][$v1['from']] + $v1['distance'] + $routeDistance[$id2][$v1['to']][$pEnd]; $routeDistance[$id1][$pStart][$v2['from']] + $v2['distance'] + $routeDistance[$id2][$v2['to']][$pEnd]; $routeDistance[$id1][$pStart][$v3['from']] + $v3['distance'] + $routeDistance[$id2][$v3['to']][$pEnd]; $ routeDistance [$ id1] [$ pStart] [$ v1 ['from']] - distance inside the route.
$ v1 ['distance'] - how much time is spent on transplantation, also in abstract units.
Accordingly, the minimum value of the calculated amounts, this will be our desired path. Next, we restore the stops that are inside the route, but are located between the point of entry into the route and the exit from it.
Example
For convenience, we choose several routes:

We roll up the routes to points and get the graph:

Suppose we need to go from 2 to 5 routes.
According to our graph we get this sample paths:

Further we work with the received routes. We need to know which route is the fastest.
Calculation of the value of the "attractiveness" of the route:
- We take the stop of the start of the route and all possible stops of the transfer to another route. According to the route_distance table, we find the length of the path from the start stop within the route to the stop of the transfer.
- Now you need to take into account the time for transplantation. Add to the calculated length in accordance with the table route_cross_point are long between the stop with which we are transplanted and the stop at which we are transplanted.
- Repeat for each route.
Take the first line of our sample.

$ routeDistance [2] [p.1] [p.3] + d1 + $ routeDistance [3] [p.5] [p.6] + d3 + $ routeDistance [5] [p.7] [p.8 ] = (float)
$ routeDistance [2] [p.1] [p.4] + d2 + $ routeDistance [3] [p.5] [p.6] + d3 + $ routeDistance [5] [p.7] [p.8 ] = (float)
$ routeDistance - the distance within the route.
d * - time to transfer.
p.1 - stop where we are going.
p.8 - stop where we are going.
d1 - the distance between p.3 and p.5
The minimum number is the best way.
What is missing and how you can develop:
- as long as the algorithm does not take into account the existing road network and does not lay a pedestrian route from point A to the transport stop and, accordingly, from the last public transport stop from the received route to point B;
- of course, you can further consider the cost of routes and, if necessary, enter the optional selection of criteria by which to choose a route (minimum cost, time, transfers, etc.), while by default we consider the target criterion to be minimum transfers;
- if they had entered fares depending on the length of the path, then also in the algorithm there would not be much to add;
Sources download . Unpack The path should not contain Russian characters.
Source: https://habr.com/ru/post/188364/
All Articles