About one elegant design

Introduction

I'll start the article by telling you how I became acquainted with this elegant design. Being engaged in Olympiad programming, my teacher and I solved many interesting problems. Then one day I came across the following task:

Print in ascending order all irreducible fractions whose denominator does not exceed n, n <= 100.

When I read the condition of the problem to the end, it did not seem difficult to me (it is not). The first thing that occurred to me was simply to go through all the denominators from 2 to n and for each denominator to go through the numerators from 1 to the denominator, provided that the numerator and the denominator are mutually simple. Well, then sort them in ascending order.
')
Such a solution is correct and the task passed all tests assigned to it. However, my teacher said that the problem can be solved much more beautifully (he has already encountered this construction). So I met this wonderful construction - the Stern-Brocot tree.

Stern-Brocot Tree

The Stern-Brocaw tree was discovered independently by the German mathematician Meritz Stern and the French watchmaker Achilles Brockaw. This tree allows you to build a set of all irreducible, non-negative fractions.

First we introduce the following term: Let two fractions be given . Then fraction - called their mediant .
We will start building a tree with two fictitious fractions:
- denoting 0;
- denoting infinity "in the irreducible form."

At each subsequent iteration between fractions, their median is inserted, and the same operation is repeated for each of the resulting pairs of fractions:


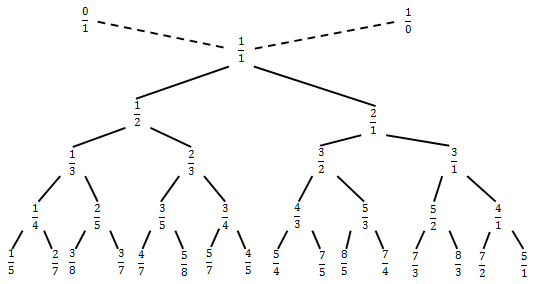
Continuing this process to infinity, we can build the whole set of irreducible, non-negative fractions.

The Stern-Brocot tree would not be so interesting, if not for its remarkable features, and he has many of them:

1. the irreducibility of fractions;
2. orderliness of fractions;
3. the presence of absolutely all fractions.

You can ask questions: why are all fractions irreducible? Why are ordered? Why can not one fraction meet more than once? The answers to these questions are quite simple. We need only a little more detail to consider the structure of this tree.

Let be - two successive fractions of the Stern-Brocot tree. You can see that for them the equality yz - xt = 1 holds (check it yourself for several pairs of fractions). We prove this statement by induction for all fractions in a tree. We take fractions as the base of induction. and for which the equality 1 * 1 - 0 * 0 = 1 - is true.

Now we will show that when inserting the mediant between fractions for which the equality yz - xt = 1 is true, it will also be true for fractions .
We have:


As you can see, both of these equations are equivalent to the original one, therefore the condition yz - xt = 1 - is an invariant for all successive fractions in a tree. Well, what does the condition yz - xt = 1 mean? It means that GCD (x, y) = GCD (z, t) = 1. In fact, the numbers x, y and z, t are coprime (If the GCD (x, y) ≠ 1, then the left-hand side would be divided into GCD , but the right side is divisible only by 1, similarly for the GCD (z, t)).

That is why fractions are irreducible, the numerator and denominator are always mutually simple. The first question answered! Go to the second!

Why fractions will be ordered? To answer this question, it suffices to show that the median of two fractions always lies between them.

Let be - two consecutive fractions in a tree and . Show that . Reducing the fraction to a common denominator and taking into account the condition we get:


Considering that the denominators of the last fractions are positive, the numerators should be negative, and this is the original inequality xt - yz ≤ 0 . Hence we conclude that the median of two fractions is always located between them (but not necessarily in the middle). Thus, we have shown the ordering of fractions in the Stern-Brocot tree.

Well and the last! Why can not we miss at least one fraction, that is, why all fractions are present in the tree?

If we had to find a certain fraction in a tree, then how would we do it? The search process is actually a binary search. We compare the desired fraction with the mediant and there are 3 cases:

1. it is equal to the mediant, the search is completed;
2. the median is greater than a fraction, then we recursively search the left subtree;
3. the median is less than a fraction, then we recursively search the right subtree.

Obviously, this process cannot be performed indefinitely. Thereby someday we will find our fraction (think for yourself why this is so) .

Farey sequence

Well, what about the original problem? It seems that the Stern-Brocot tree suits us, but there are fractions of large units in it that are redundant. However, what prevents us from taking instead of fictitious fractions and fractions ? Nothing!


This particular case of the Stern-Brocot tree is the basis for the Farey sequence.

The Farey sequence of order n is the set of all irreducible fractions between 0 and 1, the denominator of which does not exceed n, which are arranged in ascending order. Denoted by the sequence of the letter F _n .

Strictly mathematically, this sequence can be written as:

This is the Farey sequence for n = 1, ..., 5



The sequence is named after the famous geologist John Farey.

In fact, the original problem can be reformulated as follows: build an n-order Farey sequence. C # code for building it looks very simple, just 2 recursive calls:

public static void FareiSequence(int n) { Console.WriteLine("{0} / {1}", 0, 1); FareiSequence(n, 0, 1, 1, 1); Console.WriteLine("{0} / {1}", 1, 1); } private static void FareiSequence(int n, int x, int y, int z, int t) { int a = x + z, b = y + t; if (b <= n) { FareiSequence(n, x, y, a, b); Console.WriteLine("{0} / {1}", a, b); FareiSequence(n, a, b, z, t); } } 

Farey fractions can also be used to simplify mathematical expressions.

For example, you want to count the expression:



The standard way to bring to a common denominator is not interesting to us. Imagine fractions in the form of the difference between the neighboring fractions of the Farey series:



Just like that you can count this expression! On it we will finish with the Farey sequence and once again return to the Stern-Brokaw tree.

Tree as a number system

It turns out the Stern-Brocot tree can be used as a number system (symbolic method) to represent rational numbers.

But how to compare with each fraction some sequence of characters? To do this, recall the algorithm for finding a certain fraction in the tree.

Let us need to find the fraction. in a tree. We start the search with the median . The transition on the left subtree is denoted by the letter L, on the right subtree by the letter R. Thus, the number matches the LLRL character sequence (see picture).



Thus, we can associate each sequence of letters R and R with each rational fraction (or we can completely replace them with 0 and 1 to fully match the binary number system).

Approximation of real numbers by rational

If in the process of searching for a fraction in the Stern-Brocot tree, instead of a fraction, you transfer a real number, then you can get its approximation by rational fractions.

Let's try to bring the number . We get this result RRRLLLLLLLRRRRRRRRRRRRRRRRLRRRR ...

Based on this view, we can assume that fractions


serve as the simplest rational approximations to the number up and down. Thus, we can conclude that .

On this, we, perhaps, will complete our acquaintance with the Stern-Brokaw tree. I hope the article was interesting to read.