Sort in .NET
The sorting task is a classic task that any programmer should know. That is why this article is devoted to this topic - the implementation of sorting on the .NET platform. I want to talk about how array sorting works in .NET, talk about its features, implementations, and also make a small comparison with Java.
So let's start with the fact that the first versions of .NET use the quick sort algorithm by default. Therefore, a small excursion into the quick sort:
Advantages:
Disadvantages:
A naive implementation of the quick sort algorithm might look something like this:
The above sorting algorithm has the following disadvantages:
Moving on to the implementation in .NET.
')
So, consider what happens in .NET 1.0. Looking ahead, I will say that we will not see anything good here, especially for user-significant types ... (due to the lack of generalizations in particular)
And now the classes SorterObjectArray and SorterGenericArray itself:
So what's going on here? Following code
this is nothing more than an attempt to use the covariance of arrays, which, as is known, works only for reference types. It turns out that SorterObjectArray is used for reference types, and SorterGenericArray is used for significant types. But wait, what is the difference between these classes? As you can see, they differ only in the way the array elements are accessed. For meaningful types, the GetValue and SetValue methods are used, which, as you know, are very slow ... It turns out that an array of integers will be sorted for a very long time (because an integer is a significant type)? Not! An array of integers sorted quickly, and very quickly. It's all about the following code.
Of interest is the Array.TrySZSort method. This method calls the native sorting implementation implemented in C ++ in the CLR itself. And it works for primitive types when we use the standard logic of comparing elements, that is, when comparer == Comparer.Default || comparer == null.
And here is the native implementation:
As you can see, native sorting works only for primitive types. These include all numeric types + boolean + character. And for significant custom types, everything will work deplorably slowly.
We now turn to the consideration of the implementation of the sorting algorithm itself. We will consider the implementation in the SorterObjectArray class, since the native implementation and the implementation for the relevant types are similar.
1. The middle of the array is always taken as the reference element:
This is not good, because with poor input data, the execution time of the algorithm can become quadratic. In addition, the middle is taken according to the formula num1 + num2 >> 1, which can lead to an overflow of type int. The same mistake was made in the binary search and sorting algorithm in Java ( link to the bug ).
As you will see in the next versions of .NET this flaw will be fixed.
2. In order to avoid stack overflow, this implementation provides optimization that eliminates one branch of recursion: instead of calling the recursive separation procedure for both found subarrays after dividing the array, the recursive call is made only for the smaller subarray, and the larger one is processed in a loop in within the same procedure call. From the point of view of efficiency, on average, there is practically no difference: the overhead costs for an additional recursive call and for organizing the comparison of the lengths of subarrays and the cycle are approximately of the same order. But the depth of recursion, under no circumstances will exceed log 2 n, and in the worst case of a degenerate separation, it will generally be no more than 2 - all processing will take place in a cycle of the first level of recursion.
New implementation has undergone minor changes. Since there are generalizations in .NET 2.0, I will provide a generalized sorting option.
But the actual method that sorts
It should be said that there is still an optimization for the built-in primitive types, despite the presence of generalizations (see the comments of the developers). That is, primitive types still use native sorting.
Now the median from the first, middle and last elements of the array is taken as the reference element now, not the middle of the array.
In addition, the middle is now calculated by the formula index1 + (index2 - index1 >> 1), which eliminates errors associated with overflow.
Otherwise, everything is still intact.
Now a small digression: let us need to sort the array of integers in descending order. How will you do it?
Considering the above, the following code
on my computer it works about 3 times faster than
You may be confused by the fact that the Array.Reverse method is not generalized, which means that it will work slowly with significant types (packaging and GetValue, SetValue methods), but if you look at its implementation, we will again see optimization for the built-in significant types, namely calls the native Array.TrySZReverse method, which looks like this:
In general, the optimization in the standard library is waiting for us around every corner.
By the way, it is very strange that there is no generalized version of this method. There is a Reverse method as an extension method for Enumerable, but its disadvantage is that it does not do it in place. It turns out that a call to Array.Reverse on an array of user-significant types always leads to autoboxing.
The algorithm has not changed.
The most interesting begins here!
But before proceeding to the consideration of the algorithm, I must say a few words about the deployment of .NET 4.5. For a complete understanding of the situation I advise you to read this article (unfortunately, in English). When installing VS 2012, that is, when installing .NET 4.5, it replaces build 4 framework. In fact, this means that even when you are now writing to .NET 4, you are using .NET 4.5 assemblies. It turns out an interesting thing: before installation 4.5 you use one sorting algorithm, after installation you use another algorithm, and everything happens without your knowledge.
To understand what is actually happening, take a look at the code from .NET 4.5:
As you can see, the method is worth checking for what .NET we work in: if it is 4.5, then we use IntrospectiveSort if it is 4.0 then DepthLimitedQuickSort.
Let's find out how DepthLimitedQuickSort differs from sorting, which was used in .NET 4.0 before installing VS 2012. Let's look at the code of this method:
As you can see, this is the same quick sort with the exception of one: the algorithm switches to pyramidal sorting if we exhaust the recursion depth, which is 32 by default.
But actually pyramid sorting:
The DepthLimitedQuickSort algorithm is nothing but IntroSort.
Introsort or introspective sorting is a sorting algorithm proposed by David Musser in 1997. It uses a quick sort and switches to pyramid sorting when the depth of recursion exceeds a predetermined level. This approach combines the advantages of both methods with the worst case of O (n log n) and speed, comparable to the quick sort. Since both algorithms use comparisons, this algorithm also belongs to the class of sorting based on comparisons.
Now let's take a look at what happens in IntrospectiveSort. In fact, this is the same introspective sorting only more optimized. By the way, MSDN still says that it uses quick sort.
Now sorting in arrays is a mixture of sorting: sorting by inserts, quick sorting and pyramidal sorting.
The use of Introsort has a positive effect on performance, since in real-life tasks, data are partially ordered, and sorting by inserts works very quickly on such data, as is well known.
In terms of sorting, Java is quite different from .NET. However, as in .NET in Java, the algorithm also changed.
As you know, quick sorting is unstable, which is a disadvantage when sorting reference types. Since Java is “like objects”, this problem is exacerbated, so merge sort is used to sort reference types. This sorting is stable and guarantees O (n logn) runtime in the worst case, however, it also requires O (n) additional memory.
Since the stability problem concerns only reference types, for primitives it does not matter whether we change items with one key or not. Therefore, to sort primitives, Java uses an advanced quick sort algorithm, DualPivotQuicksort. Normal Quicksort divides an array into two segments, selecting a random element P. Then sorts the array so that all elements less than P fall into the first segment, and the rest into the second. Then the algorithm is recursively repeated on the first and second segments. DualPivotQuicksort divides an array into three segments, instead of two. As a result, the number of operations to move the elements of the array is significantly reduced.
In Java 7, the algorithm for sorting reference types has changed to TimSort.
Timsort is a hybrid sorting algorithm that combines sorting by inserts and merge sorting, published in 2002 by Tim Peters. Currently Timsort is a standard sorting algorithm in Python, OpenJDK 7 and implemented in Android JDK 1.5. The basic idea of the algorithm is that in the real world, sortable data files often contain ordered subarrays. On such data, Timsort is significantly faster than many sorting algorithms.
Timsort — , 30 .
? , , Java? , .NET? .NET, , , , , , 4 , , , , .
.NET , , . , . , . I hope the article was helpful.
So let's start with the fact that the first versions of .NET use the quick sort algorithm by default. Therefore, a small excursion into the quick sort:
Advantages:
- One of the fastest (in practice) of general-purpose internal sorting algorithms;
- Easy to implement;
- Requires only O (logn) additional memory for its work (not improved recursive algorithm in the worst case O (n) memory);
- Goes well with caching and virtual memory.
Disadvantages:
- It degrades greatly in speed to O (n 2 ) with unsuccessful selections of supporting elements, which can happen with unsuccessful input data. This can be avoided by choosing a supporting element in an accidental, rather than a fixed way;
- A naive implementation of the algorithm can lead to a stack overflow error, since it may need to make O (n) nested recursive calls. In improved implementations, in which the recursive call occurs only for sorting by the smaller of the two parts of the array, the recursion depth is guaranteed not to exceed O (logn);
- Unstable - if stability is required, you have to expand the key.
A naive implementation of the quick sort algorithm might look something like this:
Naive QuickSort
public void QuickSort(int left, int right) { int l = left; int r = right; int avg = array[(l + r) / 2)]; do { while (array[l] < avg) ++l; while (array[r] > avg) --r; if (l <= r) { if (l < r) { int temp = array[l]; array[l] = array[r]; array[r] = temp; } ++l; --r; } } while (l <= r); if (left < r) QuickSort(left, r); if (l < right) QuickSort(l, right); } The above sorting algorithm has the following disadvantages:
- Since the reference element is chosen as the middle of the array, it is possible that this will always be a maximum, as a result of which the array will be divided into two parts of length n - 1 and 1 and the speed of the algorithm will degrade to O (n 2 );
- Under the above conditions, the recursion depth reaches O (n), as a result of which, for large n, a software stack may overflow;
- The algorithm is unstable, that is, it changes the elements with the same values. This does not affect the example of sorting numbers, but if we sort an array of objects by some property, this is significant, because as a result of several calls to the Sort method, we get an array of elements of which differ in order.
Moving on to the implementation in .NET.
')
.NET 1.0
So, consider what happens in .NET 1.0. Looking ahead, I will say that we will not see anything good here, especially for user-significant types ... (due to the lack of generalizations in particular)
public static void Sort(Array array) { Array.Sort(array, (Array) null, array.GetLowerBound(0), array.Length, (IComparer) null); } public static void Sort(Array keys, Array items, int index, int length, IComparer comparer) { if (length > 1) { if (comparer == Comparer.Default || comparer == null) { if(TrySZSort(array, null, index, index + length - 1)) { return; } } object[] keys1 = keys as object[]; object[] items1 = (object[]) null; if (keys1 != null) items1 = items as object[]; if (keys1 != null && (items == null || items1 != null)) new Array.SorterObjectArray(keys1, items1, comparer).QuickSort(index, index + length - 1); else new Array.SorterGenericArray(keys, items, comparer).QuickSort(index, index + length - 1); } And now the classes SorterObjectArray and SorterGenericArray itself:
SorterObjectArray
private class SorterObjectArray { private object[] keys; private object[] items; private IComparer comparer; public SorterObjectArray(object[] keys, object[] items, IComparer comparer) { if (comparer == null) comparer = (IComparer)Comparer.Default; this.keys = keys; this.items = items; this.comparer = comparer; } public virtual void QuickSort(int left, int right) { do { int left1 = left; int right1 = right; object obj1 = this.keys[left1 + right1 >> 1]; do { while (this.comparer.Compare(this.keys[left1], obj1) < 0) ++left1; while (this.comparer.Compare(obj1, this.keys[right1]) < 0) --right1; if (left1 <= right1) { if (left1 < right1) { object obj2 = this.keys[left1]; this.keys[left1] = this.keys[right1]; this.keys[right1] = obj2; if (this.items != null) { object obj3 = this.items[left1]; this.items[left1] = this.items[right1]; this.items[right1] = obj3; } } ++left1; --right1; } else break; } while (left1 <= right1); if (right1 - left <= right - left1) { if (left < right1) this.QuickSort(left, right1); left = left1; } else { if (left1 < right) this.QuickSort(left1, right); right = right1; } } while (left < right); } } SorterGenericArray
private class SorterGenericArray { private Array keys; private Array items; private IComparer comparer; public SorterGenericArray(Array keys, Array items, IComparer comparer) { if (comparer == null) comparer = (IComparer)Comparer.Default; this.keys = keys; this.items = items; this.comparer = comparer; } public virtual void QuickSort(int left, int right) { do { int num1 = left; int num2 = right; object obj1 = this.keys.GetValue(num1 + num2 >> 1); do { while (this.comparer.Compare(this.keys.GetValue(num1), obj1) < 0) ++num1; while (this.comparer.Compare(obj1, this.keys.GetValue(num2)) < 0) --num2; if (num1 <= num2) { if (num1 < num2) { object obj2 = this.keys.GetValue(num1); this.keys.SetValue(this.keys.GetValue(num2), num1); this.keys.SetValue(obj2, num2); if (this.items != null) { object obj3 = this.items.GetValue(num1); this.items.SetValue(this.items.GetValue(num2), num1); this.items.SetValue(obj3, num2); } } ++num1; --num2; } else break; } while (num1 <= num2); if (num2 - left <= right - num1) { if (left < num2) this.QuickSort(left, num2); left = num1; } else { if (num1 < right) this.QuickSort(num1, right); right = num2; } } while (left < right); } } So what's going on here? Following code
object[] keys1 = keys as object[]; object[] items1 = (object[]) null; if (keys1 != null) items1 = items as object[]; this is nothing more than an attempt to use the covariance of arrays, which, as is known, works only for reference types. It turns out that SorterObjectArray is used for reference types, and SorterGenericArray is used for significant types. But wait, what is the difference between these classes? As you can see, they differ only in the way the array elements are accessed. For meaningful types, the GetValue and SetValue methods are used, which, as you know, are very slow ... It turns out that an array of integers will be sorted for a very long time (because an integer is a significant type)? Not! An array of integers sorted quickly, and very quickly. It's all about the following code.
if (length > 1) { if (comparer == Comparer.Default || comparer == null) { if(TrySZSort(array, null, index, index + length - 1)) return; } } Of interest is the Array.TrySZSort method. This method calls the native sorting implementation implemented in C ++ in the CLR itself. And it works for primitive types when we use the standard logic of comparing elements, that is, when comparer == Comparer.Default || comparer == null.
And here is the native implementation:
Native TrySZSort
FCIMPL4(INT32, ArrayHelper::TrySZSort, ArrayBase * keys, ArrayBase * items, UINT32 left, UINT32 right) // if (keys->GetRank() != 1 || keys->GetLowerBoundsPtr()[0] != 0) return FALSE; // TypeHandle keysTH = keys->GetElementTypeHandle(); // const CorElementType keysElType = keysTH.GetSigCorElementType(); if (!CorTypeInfo::IsPrimitiveType(keysElType)) return FALSE; if (items != NULL) { TypeHandle itemsTH = items->GetElementTypeHandle(); if (keysTH != itemsTH) return FALSE; // Can't currently handle sorting different types of arrays. } // if (left == right || right == 0xffffffff) return TRUE; // ++. switch(keysElType) { case ELEMENT_TYPE_I1: // 1- (sbyte) ArrayHelpers<I1>::QuickSort((I1*) keys->GetDataPtr(), (I1*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_U1: // 1- (byte) case ELEMENT_TYPE_BOOLEAN: // (bool) ArrayHelpers<U1>::QuickSort((U1*) keys->GetDataPtr(), (U1*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_I2: // 2- (short) ArrayHelpers<I2>::QuickSort((I2*) keys->GetDataPtr(), (I2*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_U2: // 2- (ushort) case ELEMENT_TYPE_CHAR: // (char) ArrayHelpers<U2>::QuickSort((U2*) keys->GetDataPtr(), (U2*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_I4: // 4- (int) ArrayHelpers<I4>::QuickSort((I4*) keys->GetDataPtr(), (I4*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_U4: // 4- (uint) ArrayHelpers<U4>::QuickSort((U4*) keys->GetDataPtr(), (U4*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_R4: // 4- (float) ArrayHelpers<R4>::QuickSort((R4*) keys->GetDataPtr(), (R4*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_I8: // 8- (long) ArrayHelpers<I8>::QuickSort((I8*) keys->GetDataPtr(), (I8*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_U8: // 8- (ulong) ArrayHelpers<U8>::QuickSort((U8*) keys->GetDataPtr(), (U8*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_R8: // 8- (double) ArrayHelpers<R8>::QuickSort((R8*) keys->GetDataPtr(), (R8*) (items == NULL ? NULL : items->GetDataPtr()), left, right); break; case ELEMENT_TYPE_I: // (IntPtr) case ELEMENT_TYPE_U: // (UIntPtr) // In V1.0, IntPtr & UIntPtr are not fully supported types. They do // not implement IComparable, so searching & sorting for them should // fail. In V1.1 or V2.0, this should change. return FALSE; default: return FALSE; } return TRUE; } Native QuickSort
// - template <class KIND> class ArrayHelpers { static void QuickSort(KIND keys[], KIND items[], int left, int right) { do { int i = left; int j = right; KIND x = keys[(i + j) >> 1]; do { while (Compare(keys[i], x) < 0) i++; while (Compare(x, keys[j]) < 0) j--; if (i > j) break; if (i < j) { KIND key = keys[i]; keys[i] = keys[j]; keys[j] = key; if (items != NULL) { KIND item = items[i]; items[i] = items[j]; items[j] = item; } } i++; j--; } while (i <= j); if (j - left <= right - i) { if (left < j) QuickSort(keys, items, left, j); left = i; } else { if (i < right) QuickSort(keys, items, i, right); right = j; } } while (left < right); } }; As you can see, native sorting works only for primitive types. These include all numeric types + boolean + character. And for significant custom types, everything will work deplorably slowly.
We now turn to the consideration of the implementation of the sorting algorithm itself. We will consider the implementation in the SorterObjectArray class, since the native implementation and the implementation for the relevant types are similar.
1. The middle of the array is always taken as the reference element:
object obj1 = this.keys[left1 + right1 >> 1]; This is not good, because with poor input data, the execution time of the algorithm can become quadratic. In addition, the middle is taken according to the formula num1 + num2 >> 1, which can lead to an overflow of type int. The same mistake was made in the binary search and sorting algorithm in Java ( link to the bug ).
As you will see in the next versions of .NET this flaw will be fixed.
2. In order to avoid stack overflow, this implementation provides optimization that eliminates one branch of recursion: instead of calling the recursive separation procedure for both found subarrays after dividing the array, the recursive call is made only for the smaller subarray, and the larger one is processed in a loop in within the same procedure call. From the point of view of efficiency, on average, there is practically no difference: the overhead costs for an additional recursive call and for organizing the comparison of the lengths of subarrays and the cycle are approximately of the same order. But the depth of recursion, under no circumstances will exceed log 2 n, and in the worst case of a degenerate separation, it will generally be no more than 2 - all processing will take place in a cycle of the first level of recursion.
.NET 2.0
New implementation has undergone minor changes. Since there are generalizations in .NET 2.0, I will provide a generalized sorting option.
public static void Sort<T>(T[] array, int index, int length, IComparer<T> comparer) { // TrySZSort . // Int32.CompareTo "<" ">". if (length <= 1 || (comparer == null || comparer == Comparer<T>.Default) && Array.TrySZSort((Array) array, (Array) null, index, index + length - 1)) return; ArraySortHelper<T>.Default.Sort(array, index, length, comparer); } But the actual method that sorts
Quicksort
private static void SwapIfGreaterWithItems(T[] keys, IComparer<T> comparer, int a, int b) { if (a == b || comparer.Compare(keys[a], keys[b]) <= 0) return; T obj = keys[a]; keys[a] = keys[b]; keys[b] = obj; } internal static void QuickSort(T[] keys, int left, int right, IComparer<T> comparer) { do { int index1 = left; int index2 = right; int index3 = index1 + (index2 - index1 >> 1); ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index3); ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index2); ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index3, index2); T obj1 = keys[index3]; do { while (comparer.Compare(keys[index1], obj1) < 0) ++index1; while (comparer.Compare(obj1, keys[index2]) < 0) --index2; if (index1 <= index2) { if (index1 < index2) { T obj2 = keys[index1]; keys[index1] = keys[index2]; keys[index2] = obj2; } ++index1; --index2; } else break; } while (index1 <= index2); if (index2 - left <= right - index1) { if (left < index2) ArraySortHelper<T>.QuickSort(keys, left, index2, comparer); left = index1; } else { if (index1 < right) ArraySortHelper<T>.QuickSort(keys, index1, right, comparer); right = index2; } } while (left < right); } It should be said that there is still an optimization for the built-in primitive types, despite the presence of generalizations (see the comments of the developers). That is, primitive types still use native sorting.
Now the median from the first, middle and last elements of the array is taken as the reference element now, not the middle of the array.
int index3 = index1 + (index2 - index1 >> 1); // ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index3); ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index1, index2); ArraySortHelper<T>.SwapIfGreaterWithItems(keys, comparer, index3, index2); T obj1 = keys[index3]; In addition, the middle is now calculated by the formula index1 + (index2 - index1 >> 1), which eliminates errors associated with overflow.
Otherwise, everything is still intact.
Now a small digression: let us need to sort the array of integers in descending order. How will you do it?
Considering the above, the following code
Array.Sort(a); Array.Reverse(a); on my computer it works about 3 times faster than
Array.Sort(a, (x, y) => -x.CompareTo(y)) You may be confused by the fact that the Array.Reverse method is not generalized, which means that it will work slowly with significant types (packaging and GetValue, SetValue methods), but if you look at its implementation, we will again see optimization for the built-in significant types, namely calls the native Array.TrySZReverse method, which looks like this:
Reverse
template <class KIND> static void Reverse(KIND array[], UINT32 index, UINT32 count) { if (count == 0) { return; } UINT32 i = index; UINT32 j = index + count - 1; while(i < j) { KIND temp = array[i]; array[i] = array[j]; array[j] = temp; i++; j--; } } }; In general, the optimization in the standard library is waiting for us around every corner.
By the way, it is very strange that there is no generalized version of this method. There is a Reverse method as an extension method for Enumerable, but its disadvantage is that it does not do it in place. It turns out that a call to Array.Reverse on an array of user-significant types always leads to autoboxing.
.NET 3.0 - .NET 4.0
The algorithm has not changed.
.NET 4.5
The most interesting begins here!
But before proceeding to the consideration of the algorithm, I must say a few words about the deployment of .NET 4.5. For a complete understanding of the situation I advise you to read this article (unfortunately, in English). When installing VS 2012, that is, when installing .NET 4.5, it replaces build 4 framework. In fact, this means that even when you are now writing to .NET 4, you are using .NET 4.5 assemblies. It turns out an interesting thing: before installation 4.5 you use one sorting algorithm, after installation you use another algorithm, and everything happens without your knowledge.
To understand what is actually happening, take a look at the code from .NET 4.5:
public void Sort(T[] keys, int index, int length, IComparer<T> comparer) { if (BinaryCompatibility.TargetsAtLeast_Desktop_V4_5) ArraySortHelper<T>.IntrospectiveSort(keys, index, length, comparer); else ArraySortHelper<T>.DepthLimitedQuickSort(keys, index, length + index - 1, comparer, 32); } As you can see, the method is worth checking for what .NET we work in: if it is 4.5, then we use IntrospectiveSort if it is 4.0 then DepthLimitedQuickSort.
Let's find out how DepthLimitedQuickSort differs from sorting, which was used in .NET 4.0 before installing VS 2012. Let's look at the code of this method:
DepthLimitedQuickSort
internal static void DepthLimitedQuickSort(T[] keys, int left, int right, IComparer<T> comparer, int depthLimit) { while (depthLimit != 0) { int index1 = left; int index2 = right; int index3 = index1 + (index2 - index1 >> 1); ArraySortHelper<T>.SwapIfGreater(keys, comparer, index1, index3); ArraySortHelper<T>.SwapIfGreater(keys, comparer, index1, index2); ArraySortHelper<T>.SwapIfGreater(keys, comparer, index3, index2); T obj1 = keys[index3]; do { while (comparer.Compare(keys[index1], obj1) < 0) ++index1; while (comparer.Compare(obj1, keys[index2]) < 0) --index2; if (index1 <= index2) { if (index1 < index2) { T obj2 = keys[index1]; keys[index1] = keys[index2]; keys[index2] = obj2; } ++index1; --index2; } else break; } while (index1 <= index2); --depthLimit; if (index2 - left <= right - index1) { if (left < index2) ArraySortHelper<T>.DepthLimitedQuickSort(keys, left, index2, comparer, depthLimit); left = index1; } else { if (index1 < right) ArraySortHelper<T>.DepthLimitedQuickSort(keys, index1, right, comparer, depthLimit); right = index2; } if (left >= right) return; } ArraySortHelper<T>.Heapsort(keys, left, right, comparer); } As you can see, this is the same quick sort with the exception of one: the algorithm switches to pyramidal sorting if we exhaust the recursion depth, which is 32 by default.
But actually pyramid sorting:
Heapsort
private static void Heapsort(T[] keys, int lo, int hi, IComparer<T> comparer) { int n = hi - lo + 1; for (int i = n / 2; i >= 1; --i) ArraySortHelper<T>.DownHeap(keys, i, n, lo, comparer); for (int index = n; index > 1; --index) { ArraySortHelper<T>.Swap(keys, lo, lo + index - 1); ArraySortHelper<T>.DownHeap(keys, 1, index - 1, lo, comparer); } } private static void DownHeap(T[] keys, int i, int n, int lo, IComparer<T> comparer) { T x = keys[lo + i - 1]; for (; i <= n / 2; { int num; i = num;}) { num = 2 * i; if (num < n && comparer.Compare(keys[lo + num - 1], keys[lo + num]) < 0) ++num; if (comparer.Compare(x, keys[lo + num - 1]) < 0) keys[lo + i - 1] = keys[lo + num - 1]; else break; } keys[lo + i - 1] = x; } The DepthLimitedQuickSort algorithm is nothing but IntroSort.
Introsort or introspective sorting is a sorting algorithm proposed by David Musser in 1997. It uses a quick sort and switches to pyramid sorting when the depth of recursion exceeds a predetermined level. This approach combines the advantages of both methods with the worst case of O (n log n) and speed, comparable to the quick sort. Since both algorithms use comparisons, this algorithm also belongs to the class of sorting based on comparisons.
Now let's take a look at what happens in IntrospectiveSort. In fact, this is the same introspective sorting only more optimized. By the way, MSDN still says that it uses quick sort.
IntroSort
private static void IntroSort(T[] keys, int lo, int hi, int depthLimit, IComparer<T> comparer) { for (; hi > lo; {int num; hi = num - 1;}) { int num = hi - lo + 1; if (num <= 16) // 16 { if (num == 1) // break; if (num == 2) // { ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi); break; } else if (num == 3) // { ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi - 1); ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi); ArraySortHelper<T>.SwapIfGreater(keys, comparer, hi - 1, hi); break; } else { ArraySortHelper<T>.InsertionSort(keys, lo, hi, comparer); // break; } } else if (depthLimit == 0) // { ArraySortHelper<T>.Heapsort(keys, lo, hi, comparer); // break; } else // { --depthLimit; num = ArraySortHelper<T>.PickPivotAndPartition(keys, lo, hi, comparer); ArraySortHelper<T>.IntroSort(keys, num + 1, hi, depthLimit, comparer); } } } PickPivotAndPartition
// private static int PickPivotAndPartition(T[] keys, int lo, int hi, IComparer<T> comparer) { int index = lo + (hi - lo) / 2; ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, index); ArraySortHelper<T>.SwapIfGreater(keys, comparer, lo, hi); ArraySortHelper<T>.SwapIfGreater(keys, comparer, index, hi); T obj = keys[index]; ArraySortHelper<T>.Swap(keys, index, hi - 1); int i = lo; int j = hi - 1; while (i < j) { do ; while (comparer.Compare(keys[++i], obj) < 0); do ; while (comparer.Compare(obj, keys[--j]) < 0); if (i < j) ArraySortHelper<T>.Swap(keys, i, j); else break; } ArraySortHelper<T>.Swap(keys, i, hi - 1); return i; } InsertionSort
// private static void InsertionSort(T[] keys, int lo, int hi, IComparer<T> comparer) { for (int index1 = lo; index1 < hi; ++index1) { int index2 = index1; T x; for (x = keys[index1 + 1]; index2 >= lo && comparer.Compare(x, keys[index2]) < 0; --index2) keys[index2 + 1] = keys[index2]; keys[index2 + 1] = x; } } Now sorting in arrays is a mixture of sorting: sorting by inserts, quick sorting and pyramidal sorting.
The use of Introsort has a positive effect on performance, since in real-life tasks, data are partially ordered, and sorting by inserts works very quickly on such data, as is well known.
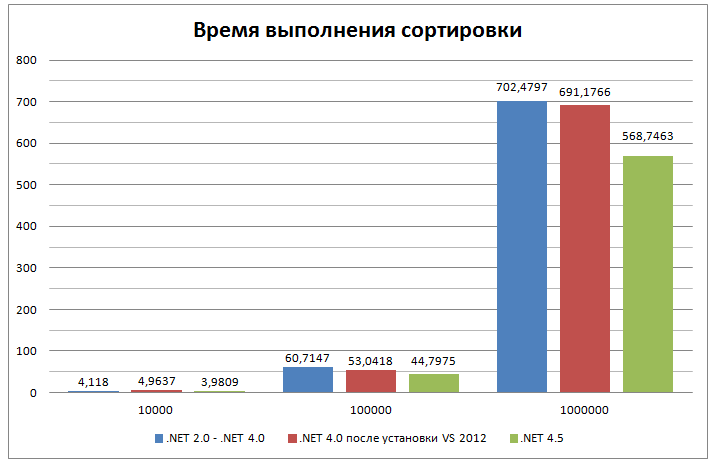
Performance comparison

Java comparison
In terms of sorting, Java is quite different from .NET. However, as in .NET in Java, the algorithm also changed.
As you know, quick sorting is unstable, which is a disadvantage when sorting reference types. Since Java is “like objects”, this problem is exacerbated, so merge sort is used to sort reference types. This sorting is stable and guarantees O (n logn) runtime in the worst case, however, it also requires O (n) additional memory.
Since the stability problem concerns only reference types, for primitives it does not matter whether we change items with one key or not. Therefore, to sort primitives, Java uses an advanced quick sort algorithm, DualPivotQuicksort. Normal Quicksort divides an array into two segments, selecting a random element P. Then sorts the array so that all elements less than P fall into the first segment, and the rest into the second. Then the algorithm is recursively repeated on the first and second segments. DualPivotQuicksort divides an array into three segments, instead of two. As a result, the number of operations to move the elements of the array is significantly reduced.
In Java 7, the algorithm for sorting reference types has changed to TimSort.
Timsort is a hybrid sorting algorithm that combines sorting by inserts and merge sorting, published in 2002 by Tim Peters. Currently Timsort is a standard sorting algorithm in Python, OpenJDK 7 and implemented in Android JDK 1.5. The basic idea of the algorithm is that in the real world, sortable data files often contain ordered subarrays. On such data, Timsort is significantly faster than many sorting algorithms.
Timsort — , 30 .
? , , Java? , .NET? .NET, , , , , , 4 , , , , .
Conclusion
.NET , , . , . , . I hope the article was helpful.
Source: https://habr.com/ru/post/188012/
All Articles