Know the complexity of the algorithms
This article talks about the runtime and memory consumption of most algorithms used in computer science. In the past, when I was preparing for an interview, I spent a lot of time exploring the Internet to search for information about the best, average and worst case search and sorting algorithms so that the question asked at the interview would not put me in a dead end. Over the past few years, I interviewed several startups from Silicon Valley, as well as some large companies such as Yahoo, eBay, LinkedIn, and Google, and every time I prepared for an interview, I thought, “Why didn’t anyone create a good cheat sheet asymptotic complexity of algorithms? ". To save your time, I created such a cheat sheet. Enjoy!

')
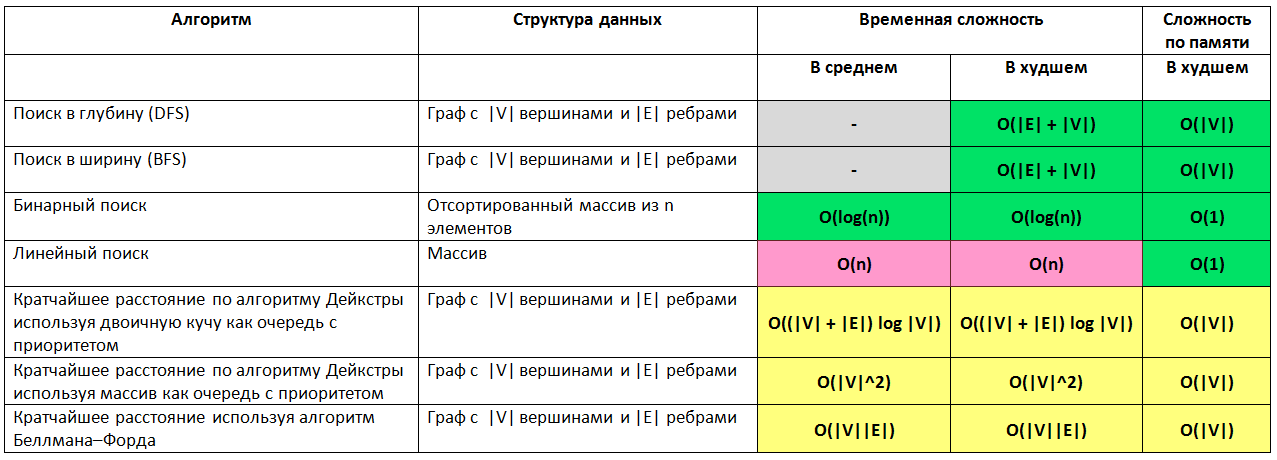
Let a graph with | V | vertices and | E | ribs then

In short, if an algorithm has complexity __ then its effectiveness is __


Search

Sorting

')
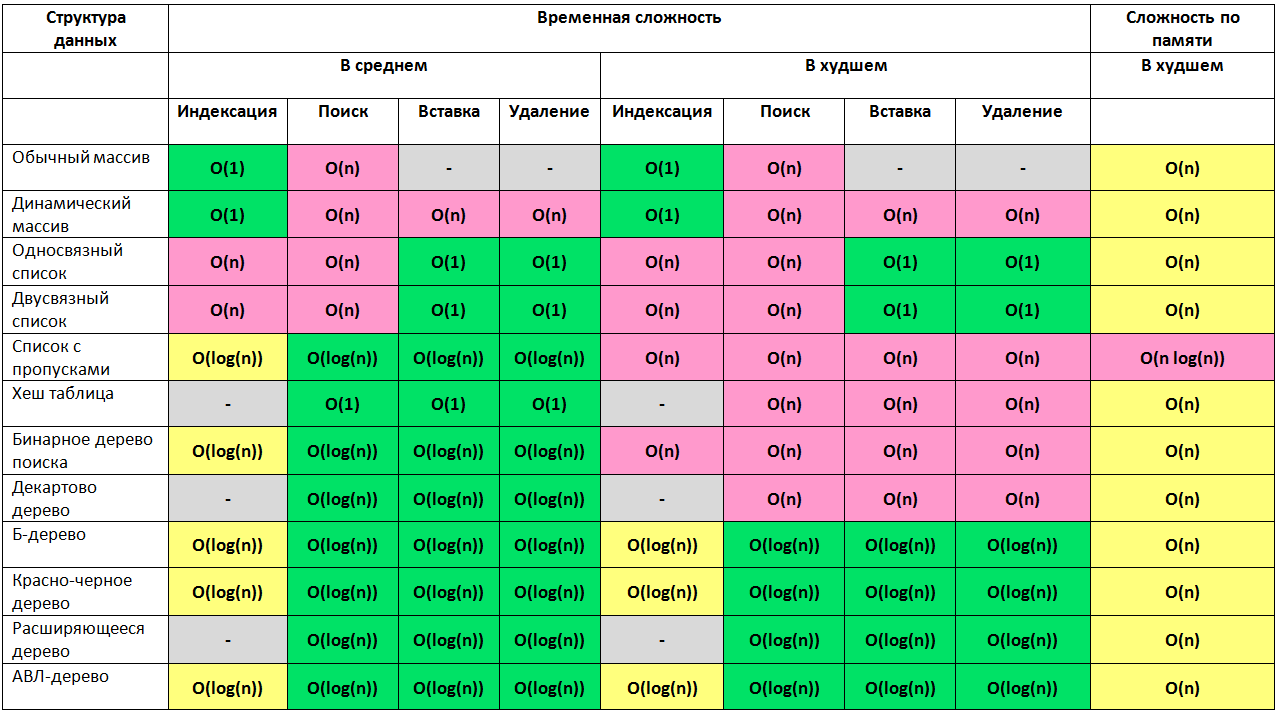
Data structures

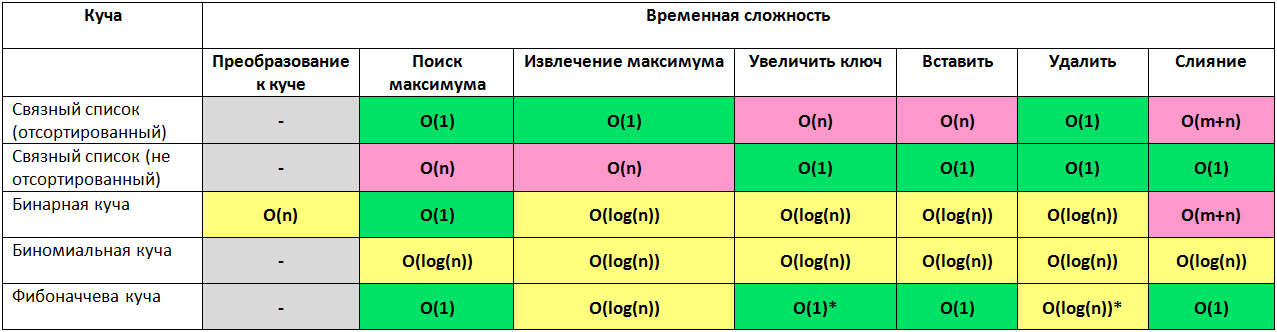
Heaps

Graph representation
Let a graph with | V | vertices and | E | ribs then

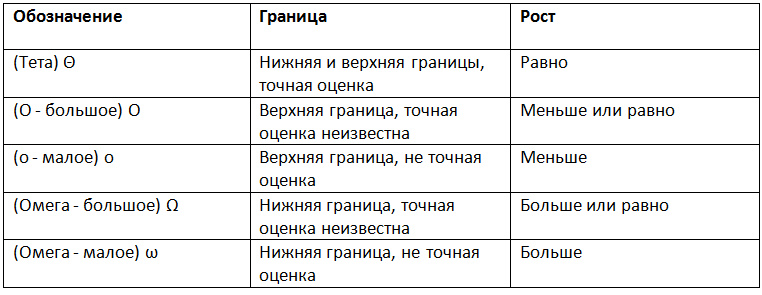
Asymptotic growth notation

- (O - large) - the upper limit, while (Omega - large) - the lower limit. Theta requires both (O - large) and (Omega - large), therefore it is an accurate estimate (it should be limited both from above and below). For example, an algorithm requiring Ω (n logn) requires at least n logn time, but the upper bound is not known. The algorithm requiring Θ (n logn) is preferable because it requires at least n logn (Ω (n logn)) and no more than n logn (O (n logn)).
- f (x) = Θ (g (n)) means that f grows in the same way as g when n goes to infinity. In other words, the growth rate f (x) is asymptotically proportional to the growth rate g (n).
- f (x) = O (g (n)). Here the growth rate is not faster than g (n). O large is most useful because it represents the worst case.
In short, if an algorithm has complexity __ then its effectiveness is __

Growth chart O - large

Source: https://habr.com/ru/post/188010/
All Articles