Algorithm for building cover sets
Frankly, before, I had never seriously studied software testing methods. However, I understand that for complete confidence that the program will work, you need to try all sorts of options for its use. The fact that it is not always possible to do this is also obvious to me. If there are specific uses, but it is impossible to check them all because of their number, try to build a set that will cover all the most used options. But what if the use of all options is equally likely? How in the minimum amount of time to detect all errors that are more likely to stumble? This task is really known, and it is often encountered, well, at least, in Yandex .
To make it clear what is at stake, imagine that we need to test any program or site. A very good example is testing a web form, say, for registration or for searching. The question arises, what errors will the user most likely encounter in it? Let us in the form there are 6 questions, for each of which there are 10 possible answers. Let's say a million users came to the page, and each of them answered uniquely. Now imagine that there is an error in the response form. If an error is detected only with a certain combination of answers to all 6 questions, then only one person will come across it. If the error takes off when typing certain answers to some 3 questions, then the number of people who discovered the error will increase to a thousand. Obviously, the fewer elements in the combination required for an error, the more people will meet with it. Accordingly, we now have a task: if we cannot detect all the errors, then let's at least find the most critical ones, that is, those that most users will stumble upon.
Thus, we must form test cases (and the smaller, the better), during the enumeration of which we will come across the most easily accessible errors. Suppose we have a lot of questions A , which we ask by the number of answers for each of them: A = {2, 3, 5, 2, ...}. Let n be the number of questions, and 1≤ m ≤n be the degree of error criticality, it is also the degree of coverage or the depth of the covering set. The smaller the value of m, the more critical the error. By setting the coverage level, we build a test suite that will detect all errors whose severity is less than a given m. If m = n, then the search for errors is reduced to the enumeration of all the options. The less we set the degree, the less test cases will be formed and the less errors we will find.

It is convenient to present the covering test suite in the form of a matrix, where the lines correspond to the test itself, and the columns represent the choice of answers to the questions. For example, take the list of questions A = {3, 3, 3, 3} and a set of eleven tests as in the picture to the right. Such a set is excellent for covering the degree m = 2, since when choosing any two columns in this set, various combinations will be sorted out between them.
How to minimize the number of lines? The first thing that occurred to me was to form a set with coverage n, that is, all test cases, and then eagerly select from it those that remove the greatest number of combinations not yet covered with m elements. So I came up with something like a greedy search for covering sets. Having decided that it was not so interesting, and, perhaps, it would turn out to be not practical, I did not follow this path.
Probably, many of you are already familiar with this task, I have never had to deal with a similar problem, and considering that the deadline was given a week, I had to seriously strain the convolutions. But it's never too late to learn. For three days and three nights, I tried to come up with an algorithm that would work best, or at least better, than Yandex Jenny . Do not think that I did not contact the search engines, I simply could not even guess what query to google. After much agony and various searches, I somehow miraculously gave birth to a method from nowhere, which was based on the consistent addition of combinations when adding a new question. Apparently, I still have a bit of a programmer mindset, since it didn’t occur to me to use any genetic algorithms, stochastic methods or anything like that, but a non-trivial, but still greedy algorithm appeared.
What was my surprise when a few days later I learned that the idea I had invented and based on, and a similar sequence of actions already exist, and the corresponding algorithm In Parameter Order is called, in other words, an algorithm based on adding a new parameter . Moreover, there are some quite good articles and even a whole book called “Review of methods for constructing covering sets” , which consider such tasks.
Here's how to classify the most famous strategies:

As you probably guessed, the algorithm described in my article is a deterministic parameterized IPO with my personal modifications. The input is A and m, the output - the minimum number of tests. The IPO strategy is divided into two consecutive parts: horizontal and vertical growth. First we add a column corresponding to the new question, then we add rows corresponding to the missing tests.
')
To begin with, we take the first m questions and sort through all the combinations between them. The output will be a matrix of m columns and the number of lines equal to A (1) * A (2) * ... A (m). Since, in any case, all combinations must be enumerated between these m columns, we cannot get a smaller number of lines. In this regard, for the best result, you just need to sort the questions by the number of options in descending order. Why? This will become clear in the future.
Let k - iteration number + m - 1. That is, the initial k = m. We now have a coverage of depth m for the first k columns. Add the following column k + 1 as follows:
Now, if all combinations are covered, then we go back to the second step, to a new horizontal growth, that is, we add a new question / column. If the number of questions is over, the algorithm ends.
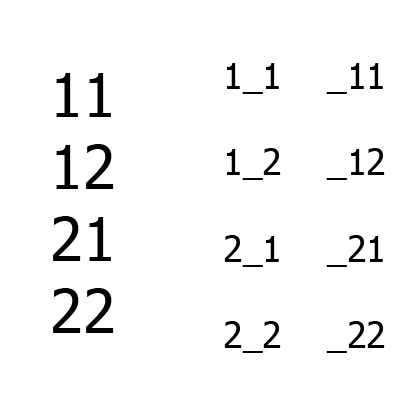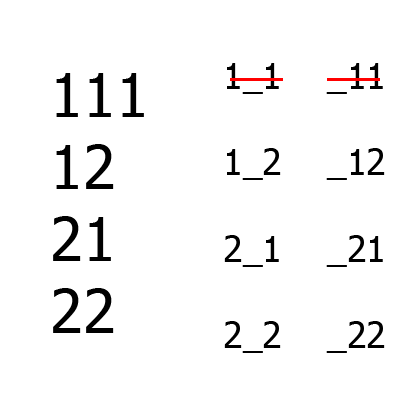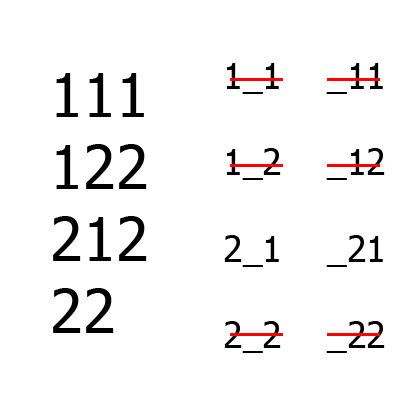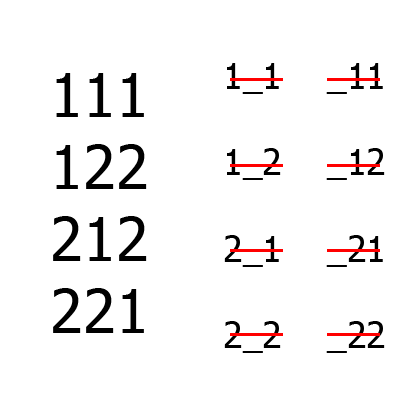
Large numbers - a set of tests, small - a set of B aka uncovered combinations (on the left - between the first and third columns, on the right - between the second and third). First the first two columns are formed, then the third is added to them. For comparison, even for such a simple example, the Jenny algorithm will build one more lines than an IPO.
However, the situation may arise more difficult when horizontal growth is not enough, and you will have to add new lines to cover the remaining combinations.
Greed in horizontal growth really gives excellent results if you sort the columns by the number of options in descending order. If you add a column with fewer options, respectively, with a smaller number of combinations with other columns, the greater the likelihood of covering these combinations in horizontal growth and avoiding vertical or at least reducing it.
Similarly, we work with vertical growth - we add a line that removes the greatest number of combinations from B. It is much more difficult to search for them here, since not one element, but a whole line changes, and this is the most difficult part of the algorithm. Therefore, as a rule, this part is avoided and add as many lines as possible, but in polynomial time. How justified the search for locally the best string is, I can’t say for sure, but in practice it gives good results.
I acted as follows: sorted in descending order of power of the set b (1), b (2), ..., b (k) are nonintersecting subsets of B, in which uncovered combinations are entered in the corresponding columns. For clarity: if B = {_11, 1_1, 1_2}, then b (1) = {1_1, 1_2}, b (2) = {_11}. This ordering is done in order to prioritize the sets with the largest number of remaining combinations. Then I took the first combination of b (1), then - any combination that does not contradict the previous combination in b (2), then - any combination that suits b (3), etc. In this example, _11 of b (2) contradicts 1_2 of b (1), but does not contradict 1_1. The search was similar to the search in depth, when it reached b (k), memorized the number taken from B combinations, returned to b (k-1), took another combination and again to b (k). The end of the search was, as in the case of horizontal growth, either the achievement of k combinations or a complete search. Then a similar search began with b (2), then with b (3) and so on until the end. Moreover, it is obvious that if it was already possible to cross out at least r combinations, then starting the search with b (kr) does not make sense. The line corresponding to the largest number of combinations taken was inserted into the list of tests, and the new one is to look for the next one.
I do not pretend to the optimality and speed of this search, but this was the only thing I invented then.
Another important modification is that if we have added not all combinations of b (1) ... b (k) to the string, that is, in one of these sets a combination was found that does not contradict the previous one, then empty ones will be formed in the string places. For example, if it does not matter to us what to insert - line 111 or 121, since the combinations _11 and _21 are already covered, then we can insert any acceptable value, but it is best to leave empty space. Why? When all combinations are accurately covered, we return to the second step or, if k = n - 1, we exit. So, in case we have to grow horizontally, we can take advantage of this empty space by inserting a value that allows you to remove any combination with a column with an empty space.


Having implemented this algorithm, I was immensely happy, since it worked better and faster than Jenny. The only, but rather big, minus IPO is that it is theoretically extremely difficult to determine in advance the exact number of rows received. That is, it works from a given depth, which should be calculated depending on the maximum number of tests. In my article I give an approximate estimate of the size of the test sets, equal to the largest number of answers to the question in the square. However, it is true only in a few cases and only with m = 2, moreover, it does not take into account the number of questions, and in fact the scatter of the real size is too large so that we can restrict ourselves to such a scanty estimate. In the case of m = 1, the number of tests coincides with the largest number of response options, for example, A (k), and for m = n - A (1) * ... * A (n). Therefore, this question remains open to me.
To make it clear what is at stake, imagine that we need to test any program or site. A very good example is testing a web form, say, for registration or for searching. The question arises, what errors will the user most likely encounter in it? Let us in the form there are 6 questions, for each of which there are 10 possible answers. Let's say a million users came to the page, and each of them answered uniquely. Now imagine that there is an error in the response form. If an error is detected only with a certain combination of answers to all 6 questions, then only one person will come across it. If the error takes off when typing certain answers to some 3 questions, then the number of people who discovered the error will increase to a thousand. Obviously, the fewer elements in the combination required for an error, the more people will meet with it. Accordingly, we now have a task: if we cannot detect all the errors, then let's at least find the most critical ones, that is, those that most users will stumble upon.
Thus, we must form test cases (and the smaller, the better), during the enumeration of which we will come across the most easily accessible errors. Suppose we have a lot of questions A , which we ask by the number of answers for each of them: A = {2, 3, 5, 2, ...}. Let n be the number of questions, and 1≤ m ≤n be the degree of error criticality, it is also the degree of coverage or the depth of the covering set. The smaller the value of m, the more critical the error. By setting the coverage level, we build a test suite that will detect all errors whose severity is less than a given m. If m = n, then the search for errors is reduced to the enumeration of all the options. The less we set the degree, the less test cases will be formed and the less errors we will find.

It is convenient to present the covering test suite in the form of a matrix, where the lines correspond to the test itself, and the columns represent the choice of answers to the questions. For example, take the list of questions A = {3, 3, 3, 3} and a set of eleven tests as in the picture to the right. Such a set is excellent for covering the degree m = 2, since when choosing any two columns in this set, various combinations will be sorted out between them.
How to minimize the number of lines? The first thing that occurred to me was to form a set with coverage n, that is, all test cases, and then eagerly select from it those that remove the greatest number of combinations not yet covered with m elements. So I came up with something like a greedy search for covering sets. Having decided that it was not so interesting, and, perhaps, it would turn out to be not practical, I did not follow this path.
Probably, many of you are already familiar with this task, I have never had to deal with a similar problem, and considering that the deadline was given a week, I had to seriously strain the convolutions. But it's never too late to learn. For three days and three nights, I tried to come up with an algorithm that would work best, or at least better, than Yandex Jenny . Do not think that I did not contact the search engines, I simply could not even guess what query to google. After much agony and various searches, I somehow miraculously gave birth to a method from nowhere, which was based on the consistent addition of combinations when adding a new question. Apparently, I still have a bit of a programmer mindset, since it didn’t occur to me to use any genetic algorithms, stochastic methods or anything like that, but a non-trivial, but still greedy algorithm appeared.
What was my surprise when a few days later I learned that the idea I had invented and based on, and a similar sequence of actions already exist, and the corresponding algorithm In Parameter Order is called, in other words, an algorithm based on adding a new parameter . Moreover, there are some quite good articles and even a whole book called “Review of methods for constructing covering sets” , which consider such tasks.
Here's how to classify the most famous strategies:

As you probably guessed, the algorithm described in my article is a deterministic parameterized IPO with my personal modifications. The input is A and m, the output - the minimum number of tests. The IPO strategy is divided into two consecutive parts: horizontal and vertical growth. First we add a column corresponding to the new question, then we add rows corresponding to the missing tests.
')
Step one.
To begin with, we take the first m questions and sort through all the combinations between them. The output will be a matrix of m columns and the number of lines equal to A (1) * A (2) * ... A (m). Since, in any case, all combinations must be enumerated between these m columns, we cannot get a smaller number of lines. In this regard, for the best result, you just need to sort the questions by the number of options in descending order. Why? This will become clear in the future.
Step two. Horizontal height
Let k - iteration number + m - 1. That is, the initial k = m. We now have a coverage of depth m for the first k columns. Add the following column k + 1 as follows:
- Create a set B - the set of all unused combinations between column k + 1 and columns 1, ..., k. Combinations within this set should be classified according to the columns to which they correspond. Consider the first line.
- What element should be added to column k + 1 in the row in question? As I said, my algorithm is greedy, and therefore we add one that will cross out as many combinations as possible from the set B. We do this: we substitute the first answer in a line and find out how many combinations from B can be crossed out with such a line. If their number is k, then the option is appropriate; if it is less, we proceed to the next one. The option that will give the largest number of deleted from B combinations and choose. From myself I would add that if several options claim to be optimal, then preference should be given to the one that will cross out the combinations with those columns with which the number of combinations not yet covered is the greatest. Then the probability of crossing out more combinations on the following lines will increase.
- Remove the covered combinations from B and go to the second paragraph, where we consider the next line. If there are no more lines, we exit.
Now, if all combinations are covered, then we go back to the second step, to a new horizontal growth, that is, we add a new question / column. If the number of questions is over, the algorithm ends.
An example of the work of the algorithm for the situation is A = {2, 2, 2}, m = 2.
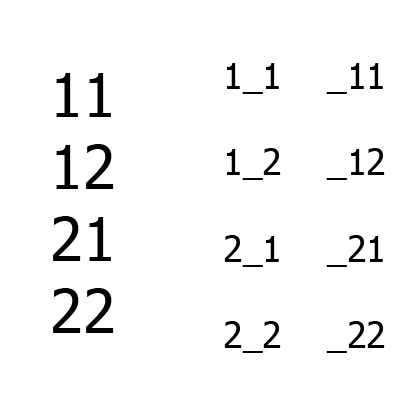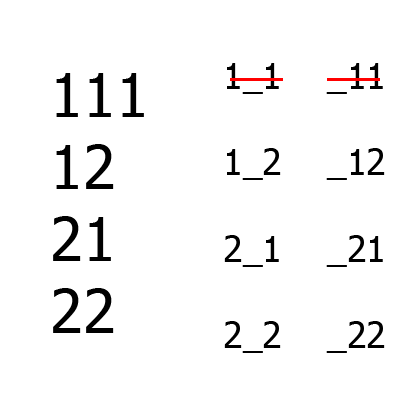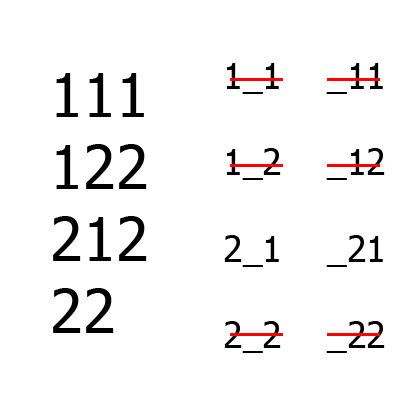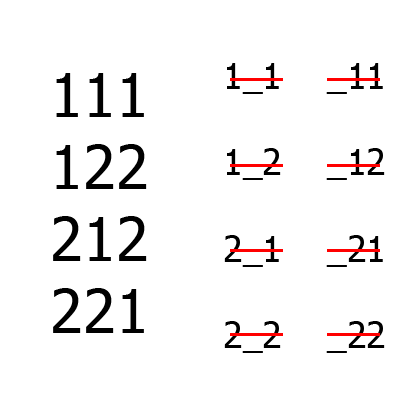
Large numbers - a set of tests, small - a set of B aka uncovered combinations (on the left - between the first and third columns, on the right - between the second and third). First the first two columns are formed, then the third is added to them. For comparison, even for such a simple example, the Jenny algorithm will build one more lines than an IPO.
However, the situation may arise more difficult when horizontal growth is not enough, and you will have to add new lines to cover the remaining combinations.
Step three. Vertical growth
Greed in horizontal growth really gives excellent results if you sort the columns by the number of options in descending order. If you add a column with fewer options, respectively, with a smaller number of combinations with other columns, the greater the likelihood of covering these combinations in horizontal growth and avoiding vertical or at least reducing it.
Similarly, we work with vertical growth - we add a line that removes the greatest number of combinations from B. It is much more difficult to search for them here, since not one element, but a whole line changes, and this is the most difficult part of the algorithm. Therefore, as a rule, this part is avoided and add as many lines as possible, but in polynomial time. How justified the search for locally the best string is, I can’t say for sure, but in practice it gives good results.
I acted as follows: sorted in descending order of power of the set b (1), b (2), ..., b (k) are nonintersecting subsets of B, in which uncovered combinations are entered in the corresponding columns. For clarity: if B = {_11, 1_1, 1_2}, then b (1) = {1_1, 1_2}, b (2) = {_11}. This ordering is done in order to prioritize the sets with the largest number of remaining combinations. Then I took the first combination of b (1), then - any combination that does not contradict the previous combination in b (2), then - any combination that suits b (3), etc. In this example, _11 of b (2) contradicts 1_2 of b (1), but does not contradict 1_1. The search was similar to the search in depth, when it reached b (k), memorized the number taken from B combinations, returned to b (k-1), took another combination and again to b (k). The end of the search was, as in the case of horizontal growth, either the achievement of k combinations or a complete search. Then a similar search began with b (2), then with b (3) and so on until the end. Moreover, it is obvious that if it was already possible to cross out at least r combinations, then starting the search with b (kr) does not make sense. The line corresponding to the largest number of combinations taken was inserted into the list of tests, and the new one is to look for the next one.
I do not pretend to the optimality and speed of this search, but this was the only thing I invented then.
Another important modification is that if we have added not all combinations of b (1) ... b (k) to the string, that is, in one of these sets a combination was found that does not contradict the previous one, then empty ones will be formed in the string places. For example, if it does not matter to us what to insert - line 111 or 121, since the combinations _11 and _21 are already covered, then we can insert any acceptable value, but it is best to leave empty space. Why? When all combinations are accurately covered, we return to the second step or, if k = n - 1, we exit. So, in case we have to grow horizontally, we can take advantage of this empty space by inserting a value that allows you to remove any combination with a column with an empty space.
An example of the operation of the algorithm for the situation is A = {3, 3, 3, 3}, m = 2.
The first iteration. To the first two columns formed, a third is added. Then two lines are added to cover the remaining combinations _23 and _31

The second iteration. Add the fourth column. Empty places are filled with random numbers.

Conclusion
Having implemented this algorithm, I was immensely happy, since it worked better and faster than Jenny. The only, but rather big, minus IPO is that it is theoretically extremely difficult to determine in advance the exact number of rows received. That is, it works from a given depth, which should be calculated depending on the maximum number of tests. In my article I give an approximate estimate of the size of the test sets, equal to the largest number of answers to the question in the square. However, it is true only in a few cases and only with m = 2, moreover, it does not take into account the number of questions, and in fact the scatter of the real size is too large so that we can restrict ourselves to such a scanty estimate. In the case of m = 1, the number of tests coincides with the largest number of response options, for example, A (k), and for m = n - A (1) * ... * A (n). Therefore, this question remains open to me.
Source: https://habr.com/ru/post/187882/
All Articles